Photonic integrated circuits (PICs)^[1] have been developed for the increasing complexity of both classical and quantum information processing, which is demanding on scalability, stability, and high-quality interference. By integrating the waveguides and controlling their coupling on a chip, basic optical elements^[2] in bulk optics can be realized on-chip with high quality, such as a beam splitter (BS), phase shifter, and polarization beam splitter (PBS)^[3,4]. Recently, a quantum C-NOT gate, quantum walk, and Boson sampling have been performed on a single chip, based on silica-on-silicon waveguides^[5,6], laser direct writing waveguides^[7,8], and plasmonic waveguides^[9,10]. There remains challenges in integrating optical devices with good performance, and the errors due to experimental imperfection will be amplified when cascading many basic integrated devices together for future quantum computing, simulation, and communication.

Among various imperfections, loss is inevitable that is generated from both the essential absorption of materials and the technical problems in fabrication. The effect of loss in bulk optics has been studied in earlier years^[11,12]. When dealing with integrated circuits, many basic optical components are integrated together, and more complex structures should attract our attention. Generally, there are off-chip insertion losses and on-chip waveguide losses. Usually, people summarize these linear losses and combine them with the inefficiency of detectors. Since quantum processes can be realized via post selection, which claims success when detecting the photons in the desired manner, so linear quantum computation can still be performed with those imperfections, and the only influence is the low success probability.

In this Letter, we studied the general loss model in the on-chip BS devices and its effects on the gate fidelities. We found that when there is an unbalanced loss (UBL) or a shared common loss (CL) channel in the BS, there will be significant errors that will affect the performance of the optical quantum processing.

For an ideal linear process supported by a quantum PIC, the relation between the input and output field can be described by a unitary matrix. It has been demonstrated that any unitary matrix can be decomposed to the product of two level matrices^[13], which meanwhile can be further decomposed to phase shifters and BSs^[14]. Figure 1(a) shows a sketch picture of a directional coupler, the physical realization of a BS, where two waveguides approach each other and exchange energy. For simplicity, we only focus on the uniform coupling regime, whose properties can be analyzed by solving the eigenmodes of the coupled waveguide at the cross section. In the weak coupling regime, two waveguides couple with each other through tunneling, which can be quantitatively described by the coupling rate C. According to the coupled mode theory, the dynamics of photon amplitude A1, A2 in two waveguides should obey ddLA1=(−iβ−γ1)A1−iCA2,(1)ddLA2=(−iβ−γ2)A2−iCA1,(2)where β is the propagation constant, γi is the damping rate, and L is the distance along the propagation direction. The coupled equations can also be expressed in vector form ddLA→=−iHA→,(3)A→=(A1A2),H=(β−iγ1CCβ−iγ2).(4)

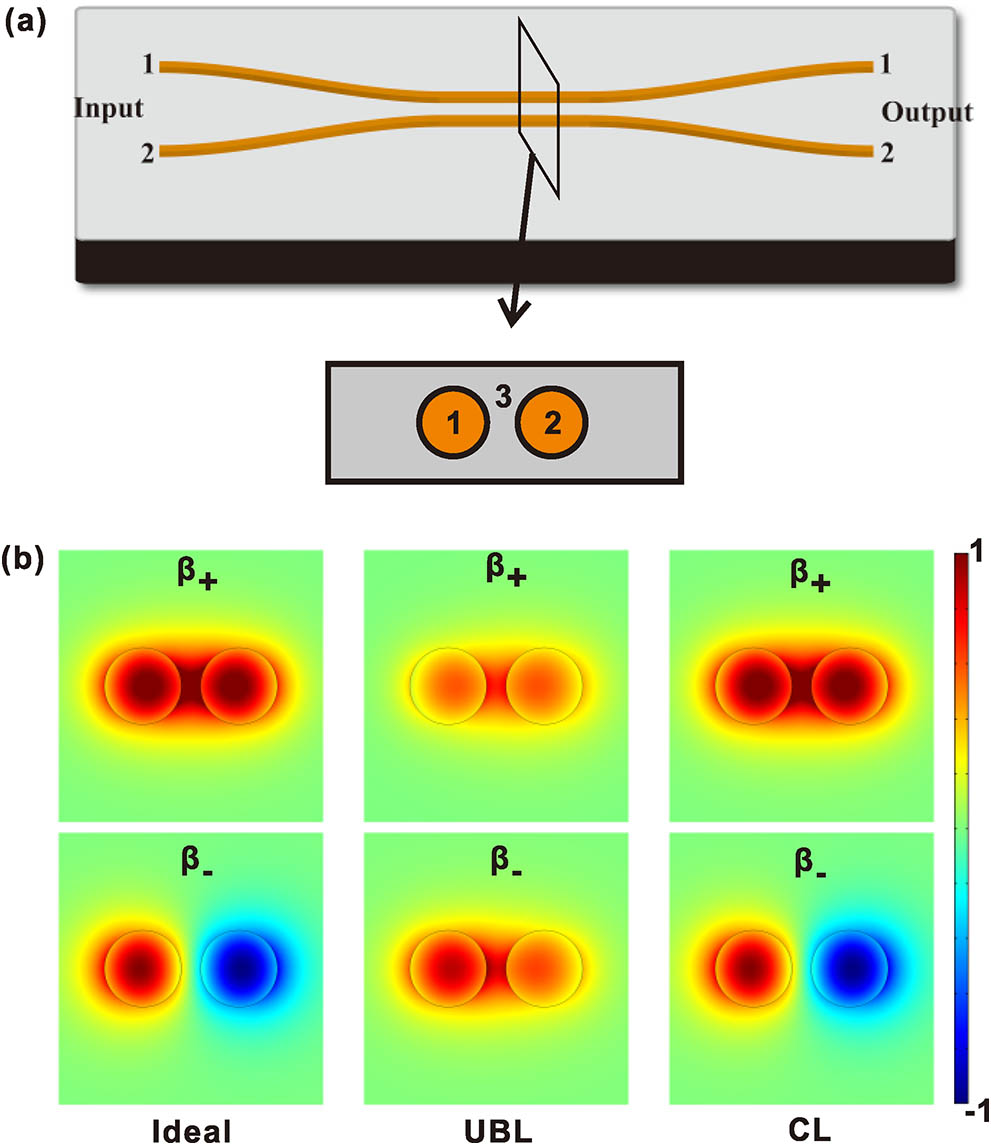
Fig. 1. Eigenmodes of coupled waveguides. (a) A schematic of a directional coupler. (b) The cross-section electric field distributions of the eigenmodes for different cases. From the left column to right, the pictures correspond to the (i) ideal case γ1,=γ2, (ii) γ1≠γ2, and material 3 is lossless, (iii) γ1=γ2 and material 3 is absorptive. For the left and right case, the two eigenmodes are orthogonal and the overlap is zero. For the middle case, the overlap of the two modes is positive.

下载图片 查看所有图片

Therefore, the eigenmodes can be solved by solving the eigenvector of H as a superposition of the field in two waveguides. If a photon is loaded to one of the waveguides corresponding to the superposition of the two eigenmodes, the photon will oscillate between the waveguides in the sine function form since the eigenvalues of the two eigenmodes are different.

In general, we assume the two waveguides and their surroundings are made by different materials, and the configurable structures can be divided into three cases: (i) two waveguides are identical, thus the propagation losses γ1=γ2, (ii) the two waveguides are made by different materials (γ1≠γ2) and the surrounding material is lossless (iii) γ1=γ2 while the surrounding material is absorptive. For case (i), the propagation loss of light in the two waveguides can be taken out as a global damping factor, thus the two waveguides couple with each other as they are ideal, except for the attenuation of the amplitude. The left column in Fig. 1(b) shows the eigenmodes for case (i), the two modes are orthogonal as the field in two waveguide are in-phase and out-of-phase, respectively, while the amplitude in the two waveguides are identical. When dealing with hybrid PICs, case (ii) should be considered. The modes in the two waveguides attenuate with different rates and exchange energy continuously with each other when they propagate forward. However, the different damping rates make them no longer orthogonal, which is explicitly shown in the middle column of Fig. 1(b). In all the cases, the two eigenmodes have different energy distributions. If material 3 is absorptive, different energy penetration to material 3 means different damping loss, corresponding to case (iii). For long coupling length, the eigenmode with a bigger loss becomes negligible compared with the one with a smaller loss. Even though the two modes are still orthogonal the different amplitudes destroy the interference. For cases (ii) and (iii), the imperfections are named as UBL and CL, respectively. From the preliminary analysis, we can judge that loss can indeed change the evolution of photonic quantum states in the PIC.

Fig. 2. (Color online) Two coupled waveguides with an unbalanced linear loss. (a) By injecting a single photon in port 1 in Fig. 1(a), the hopping probability to the outputs are plotted. Blue line: port 1. Red line: port 2. The inset shows the relative intensity eliminating the global damping factor. We set C=0.01k0 and Δγ=0.01k0. (b) The mode overlap |〈+|−〉|2 of the two eigenmodes. (c) The real (blue) and imaginary (red) part of the difference between β+ and β−. The cross point is the exceptional point. (d) L0 is the minimum coupling length to achieve 1:1 splitting. (e). Two-photon quantum interference visibility on an ideal BS with C=0.01k0. (f) Two-photon quantum interference visibility on a BS with unbalanced linear loss as a function of the coupling length. C=0.01k0 and Δγ=0.01k0. In all the figures, the units of C and γi are the free-space wave vector k0. We set C=0.01k0 for all the cases.

下载图片 查看所有图片

For case (ii), the UBL usually exists in hybrid coupled waveguides, for example two waveguides supported by dielectric and metal materials ^[15,16]. The UBL may also appear if the fabrication roughness or curvature of the two waveguides is different.

By Eq. (4), the outputs of two waveguide can be solved as A→(L)=e∫0L−iHdLA→(0)=M(L)A→(0), with L being the length of the coupling region. We obtain M(L)=e(−iβ−γ1+γ22)L×(Δγ2αcosh(αL)−sinh(αL)iCαsinh(αL)iCαsinh(αL)Δγ2αsinh(αL)+cosh(αL)),(5)where Δγ=γ1−γ2 and α=(Δγ2/4)−C2. For the bosonic operator of input ports a1,2in, the output should be (j=1,2) ajout=[M(L)]j,1a1in+[M(L)]j,2a2in+∑0∞pkck,(6)where ck is the accessible environment mode and pk is the amplitude probability satisfying ∑k|pk|2+|[M(L)]j,1|2+|[M(L)]j,2|2=1.

In Fig. 2(a), we plot the probabilities |[M(L)]j,1|2 as a function of L. These two curves still behave as a sine function oscillation accompanied by exponential decay. The inset shows the oscillation curves by eliminating the global damping factor e−(γ1+γ2/2)L. We find an unusual phenomenon that the phase between the two sine oscillations is no longer π, which is different from the ideal case. To explain the decreased phase, we investigated the change of the eigenmodes altered by such UBL. By diagonalizing matrix H, we get the eigenvalues β+, β−, and eigenvectors |+〉, |−〉, corresponding to the effective mode propagation index and the wave function of the eigenmodes, respectively. The eigenvalues are β±=β−i(γ1+γ2)2±4C2−Δγ2.(7)

First, we investigated the mode orthogonality of the eigenmodes, and plotted the overlap of the two eigenmodes |〈+|−〉|2 in Fig. 2(b). The UBL destroyed the orthogonality of the eigenmodes. As the UBL Δγ approaches C, the overlap between the two modes increases to unity, which means the two modes are almost identical. As a result, the phase difference between the two oscillations in Fig. 1(a) decreases from π to 0 and the two curves get closer. The broken mode orthogonality was also demonstrated by the change of the effective mode index of the eigenmodes. Figure 2(c) gives the real and imaginary part of the difference of β+ and β−. Δβ decreases as Δγ changes close to 2C. It should be noted that, at the critical point α=0, the two eigenmodes become totally the same, which is called the exceptional point^[17,18]. The two eigenmodes completely overlap and share the same mode index. At the exceptional point, the two-dimensional system coalesces to one dimension. By diagonalizing the Hamiltonian of the coupled system, we find that there is only one eigenvector (i,1)T. In an isolated Hermitian system, coupled modes or energy levels will repel each other and the levels will never cross, which is called anti-crossing. In such a non-Hermitian system, the two levels coalesce to one level, although they are not degenerate and the two-dimensional system is reduced to one^[18], which has been observed in coupled microcavities^[19] and coupled waveguides^[20] with loss-gain. Here we show that coupled waveguides with only loss also have this phenomenon.

Another important change induced by the UBL is the increase of the oscillation periods of the intensity lines, compared to the ideal case. In Fig. 2(a), the increase of the oscillation periods means the coupling strength between the waveguides has been weakened by the loss difference Δγ. For example, to get a 1:1 BS, a longer coupling length is required. Figure 2(d) gives the relation between the minimum coupling length L0 for a 1:1 BS and the UBL Δγ. We can conclude that the effective coupling strength is weakened by the unbalanced linear independent loss. Note that γ1=γ2 is the zero point in the curves in Fig. 2, which behaves the same with the ideal case, except for the decay of the total energy.

In quantum optics, the interference of indistinguishable photons in a waveguide circuit is very sensitive to the phase relation between different input and output ports, which reflects in the phase difference between different elements of the process matrix M(L). One basic process to test the quantum nature of the circuit is HOM interference^[21]. By injecting two indistinguishable photons from the inputs, we can calculate the second-order quantum correlation Γq of the output state. Comparing the quantum correlation with the classical correlation Γc, the contrast can be used to measure the performance of the BS for quantum operation. Here, we use visibility V to characterize the performance of a BS in quantum optics, V=1−Γq/Γc.(8)

From Eq. (6), we can calculate the second-order classical and quantum correlation 〈a1out†a1outa2out†a2out〉 of the output state as Γc=|M11M22|2+|M12M21|2,(9)Γq=|M11M22+M12M21|2,(10)

As is shown in Fig. 2(e), the visibility of an ideal coupler oscillates between 0 and 1 periodically, with the increasing of the coupling length L of the BS. However, in the case with UBL, the adjusted phase relation makes the quantum interference different. The relation between visibility and coupling length is plotted in Fig. 2(f). Two main obvious differences can be found, (1) the period of oscillation becomes large, which is consistent with the result of single-photon analysis, (2) the visibility appears to be negative in some coupling regions. This result is totally different from the HOM interference on an ideal BS, in which case the second-order quantum correlation is always smaller than the classical correlation. As the loss difference Δγ approaches the exceptional point, the second-order quantum correlation becomes twice the classical correlation, thus the visibility gets its minimum value −1. An HOM dip can never be observed at the point, and a peak is observed instead. The reason is that loss destroyed the orthogonality of the non-Hermitian system, so quantum coherence cannot be fully maintained in these devices.

From the analysis for single- and two-photon states, we can conclude that the UBL not only influences the efficiency of the integrated circuit but also changes the function of the circuit. On one hand, the effective coupling strength is weakened by the loss difference. As a result, a larger circuit should be designed to realize the same operation. On the other hand, the impacted phase relation leads to extraordinary interference for both the classical and quantum field. For waveguides with UBLs, the energy cannot be exchanged between the two waveguides with complete coherence. So, when designing integrated devices for quantum operation, the loss difference between different waveguides should be carefully controlled, especially for waveguides with very weak coupling strengths.

In the above paragraph, we discussed the effect of the UBL, while the coupling rate C between the waveguides is still real. However, there exists some cases that the coupling constant C is a complex number because the two coupled waveguides not only couple in the regime of the direct overlap of their modes, but also through the reservoir in the surrounding material, such as in a plasmonic circuit. To study such an effect, we add an imaginary part iC2 to the real coupling constant C1. Similar to the procedure in the UBL case, we calculate the transfer matrix elements in the CL case, where the probabilities still oscillate in the form of a sine function with opposite phase [shown in Fig. 3(a)]. The oscillations get less pronounced with an increasing L. As the coupling length becomes large enough, the two curves tend to merge to a single line and the splitting ratio of the BS approaches 1:1. Figures 3(b) and 3(c) show the properties of the eigenmodes of the CL case. Figure 3(b) indicates that the two eigenmodes are still orthogonal. The altered effective mode index is plotted in Fig. 3(c).

Fig. 3. (Color online) Single-photon and two-photon interference on a BS with shared CL. (a) Relative probability in two waveguides with single-photon input. (b) The mode overlap |〈+|−〉|2 of the two eigenmodes. (c) The real and imaginary part of β+−β−. (d) The visibility of two-photon quantum interference. The visibility becomes negative and approaches −1 as the coupling region becomes longer. Here we set the damping rate the waveguides γ=0.001k0, C1=0.01k0, and C2=0.0005k0.

下载图片 查看所有图片

We then examine the quantum performance of the two coupled waveguides with CL by calculating the visibility. As is shown in Fig. 3(d), the V of the two-photon interference decreases from 1 to −1, with the coupling length increasing to infinity. This arises because the two eigenmodes of the coupled system decrease with different rates, and the system acts as a filter. When L becomes large enough, the mode with a bigger loss can be neglected compared to the other one, thus any photon will be found with equal probability in each waveguide. To explain the visibility of −1, we consider the nonHermitian system as a subsystem of a higher-dimensional Hermitian system, where the process matrix M is only a submatrix of a unitary process, by including all environmental degrees of freedom [Eq. (6)]. The bunching nature of the photons causes Γq=2Γc when L becomes infinitely large, which leads V to be −1. Under this situation, V can be treated as a feature of the degree of non-unitary of the process matrix. The CL loss is responsible for the low quantum interference visibility in plasmonic circuits^[22], which can be avoided using dielectric loaded circuits^[9]. Recently, HOM interference showing a peak fringe was experimentally observed in the plasmonic system^[23].

We then go further to investigate how such loss influences the quantum operation of a relatively large circuit formed by BSs and phase shifters. On a real integrated optical chip, the shared loss appears to be more influential. From simple to complex, we calculated the fidelity of single-qubit operation, C-NOT gate, and arbitrary two-qubit gate suffering from shared loss. Following the quantum gate decomposition method, these gates are decomposed to BSs and phase shifters. Here, we replace the ideal BSs with BSs suffering from shared loss. The fidelity F of the gate is defined as F=min|Φ〉,U〈Φ|U†B|Φ〉〈Φ|B†U|Φ〉,(11)where |Φ〉 is the input state, U is the unitary operation of the ideal circuits, B is the real quantum operation using a BS with losses. The fidelity F is searched among all the input states and quantum operations. Here, we change the relative value of C2 to evaluate the fidelity of quantum gates. From Figs. 4(a) and 4(b), we see that the fidelity decreases fast as the imaginary part of C gets comparable to its real part. The comparison between quantum gates shown in Figs. 4(a) and 4(b) also indicates that the circuit complexity is very sensitive to the imaginary part of the coupling rate. To achieve fidelity of the two-qubit gate higher than 99%, C2<2.5×10−4C1 should be ensured. For larger quantum circuits, the dependence on C2 will be more sensitive. So when dealing with large-scale circuits supported by absorptive materials, reasonable design and quantum error correction should attract much more attention to avoid such shortcomings.

Fig. 4. (Color online) Fidelity of quantum gates formed by a BS with shared loss. All quantum gates are decomposed to BSs and phase shifters and we assume the phase shifters are ideal. The fidelity is the minimum value searched through all input quantum states. (a) The gate fidelity for a BS, single-qubit operation, and quantum C-NOT gate. (b) The minimum fidelity for any two-qubit gate and any two-qubit quantum state. In the calculations, C1=0.01k0.

下载图片 查看所有图片

In conclusion, we investigate the performance of a realistic coupled waveguide system, which is the basic element in quantum PICs. As an inevitable factor in reality, loss is a block in the way of integrating optics on-chip on a large scale. Apart from its harmful effect on the efficiency, loss also changes the physical process. By analyzing the properties of the eigenmodes and evaluating the second-order coherence of two-photon quantum interference, we quantify the performance of the coupled system. We find that unbalanced linear loss can weaken the effective coupling strength and destroy the orthogonality of the coupled waveguides. Both the unbalanced linear loss and the complex coupling between two identical waveguides result in a reduction of the visibility of the quantum interference. All these imperfections should be considered when designing and fabricating large-scale quantum PICs.