基于多核学习-密度峰值聚类的基础矩阵估计

王剑峰; 王宏伟; 闫学勤

doi:doi:10.3788/LOP57.041017

激光与光电子学进展, 2020, 57 (4): 041017, 网络出版: 2020-02-20

基于多核学习-密度峰值聚类的基础矩阵估计下载： 797次

Fundamental Matrix Estimation Based on Multiple Kernel Learning-Density Peak Clustering

论文大纲

王剑峰 ^1,*王宏伟 ^1,2,**闫学勤 ^1,***

作者单位

¹ 新疆大学电气工程学院, 新疆乌鲁木齐830047

² 大连理工大学控制科学与工程学院, 辽宁大连116024

图像处理多核学习密度峰值 γ分布图; 最优内点子集 image processing multi-kernel learning peak density γ distribution diagram; optimal internal point set

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

现有基础矩阵鲁棒估计方法存在精度不高、准确性较低等不足,基于此,提出一种利用多核学习改进密度峰值聚类的基础矩阵估计方法。首先,针对密度峰值算法需要选取参数和无法自动聚类等不足,引入多核学习和γ分布图进行改进;其次,以对极距离为特征,通过多核学习-密度峰值算法剔除匹配数据集中的异常值,得到较优内点集;最后,使用M估计法消除定位噪声误差,对内点子集进行进一步优化处理,并估计最终的基础矩阵。利用INRIA Dataset数据集对所提方法进行验证分析。结果表明:在保证匹配点信息较多的前提下,所提方法提高了基础矩阵的计算精度和准确性。

Abstract

Existing robust estimation methods of the fundamental matrix possess some limitations such as low accuracy. This study presents a fundamental matrix estimation method that uses multi-kernel learning to improve density peak clustering. First, from the viewpoint of the shortcomings in the density peak algorithm, such as the need to select parameters and inability to automatically cluster, multi-kernel learning and γ distribution map are introduced. Second, with the feature of epipolar distance, the proposed method eliminates the anomaly of the matching dataset to obtain a better internal point set. Finally, the M estimation method is used to exclude the positioning noise error, conduct further optimization processing on the internal idea set, and estimate the final base matrix. The INRIA dataset is used to validate and analyze the proposed method. Results show that the calculation accuracy and correctness of the fundamental matrix are improved using the proposed method.

1 引言

基础矩阵是对极几何的代数表达,它包含了同一场景下两个视图之间转换的内、外参数,是从两幅未校准图像中能够获得的唯一信息^[1]。基础矩阵的传统计算方法包括^[2]:线性方法、非线性方法以及鲁棒方法。线性算法包括八点法和改进的八点法等,虽然简单、快速,但是容易受到定位噪声和异常值的干扰^[3];非线性方法利用迭代法虽然可以有效减少定位噪声的影响,但不能处理异常值;随机抽样一致性(RANSAC)算法^[4]、M估计法^[5]和最小中值法(LMedS)^[6]等方法因其较好的鲁棒性受到了广大学者的喜爱,它不但能够减小定位噪声的影响,而且对于异常值有一定的处理能力(鲁棒性),然而,现有的鲁棒方法不能在保证匹配信息完全的情况下提高精度和准确性。

目前,很多学者根据鲁棒方法的不足,提出了许多改进的方法。文献[ 7]通过结合粒子群和模拟退火的全局寻优能力从多个基础矩阵中寻找最优的基础矩阵;文献[ 8]根据几何误差准则,用迭代法同时消除异常值和定位噪声的影响,在一定程度上提高了算法的效率和精度;文献[ 9]利用模糊核C-均值聚类方法,对匹配点的估计余差进行聚类以获得相对精确的内点集并估计基础矩阵,但前提是估计余差必须满足高斯分布;文献[ 10]通过对RANSAC算法进行改进,提出了随机化RANSAC(R-RANSAC)算法,该算法首先随机选取一个内点子集进行部分检验,再对通过的内点进行全局检验,有效地减少了计算量;Chum等^[11]通过对选出的内点进行局部优化提出了局部优化RANSAC(LO-RANSAC)算法。

聚类分析是根据数据特征将其归类的过程^[12]。聚类方法大致可分为4类^[13]:基于层次的聚类^[14]、基于划分的聚类、基于密度的聚类^[15],以及基于网格的聚类。密度峰值(CFDP)算法^[16]由Rodriguez等在2014年提出,主要思想是通过计算数据密度和距离对每个数据点归类。相对于基于密度的DBSCAN^[17](Density-Based Spatial Clustering of Applications with Noise)算法,CFDP算法具有设置参数少、聚类速度较快、无需指定聚类中心等优点,但仍存在无法自动聚类和阈值设置不正确时聚类效果不佳等不足。因此,本文使用多核学习改进CFDP算法进行快速聚类,得到只含有定位误差的候选内点集,对候选内点集使用M估计法得到更加精确的基础矩阵,为提高三维重建精度奠定基础。

2 对极几何及基础矩阵

2.1 对极几何

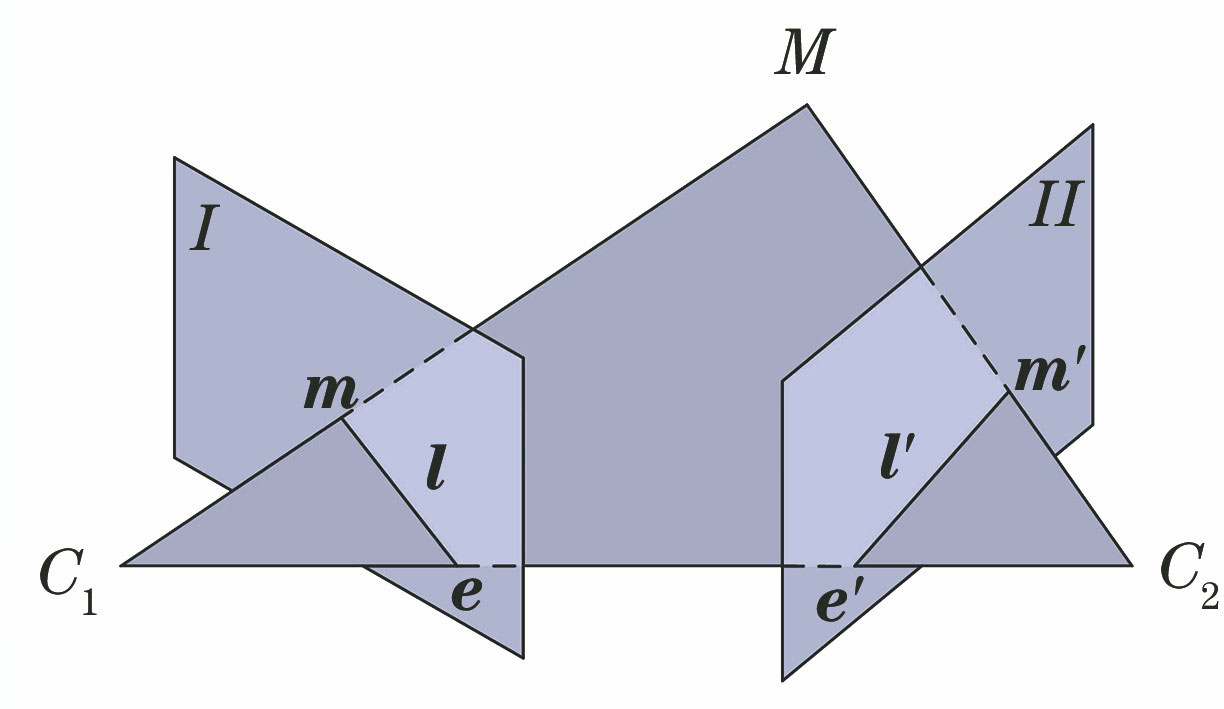
从不同角度得到的同一视点的两幅匹配图像存在一种约束关系,称其为对极几何约束^[18]。如图1所示,图中C₁和C₂为相机光心,I和Ⅱ是两个成像平面;点m与m'为世界坐标系下空间点M在不同视角下的成像点,则平面I上的点m在平面Ⅱ上的对应当点m'必然位于过点m'和e'的对极线l'上;同理,平面Ⅱ上的点m'在平面I上的对应当点m必然位于过点m和e的对极线l上;称e和e'为极线上的极点。且有下式成立:

\begin{matrix} m'^{T} Fm = 0, (1) \end{matrix}

式中:F为基础矩阵,是一个3×3维、秩为2、自由度为7的奇异矩阵。当匹配点中不包含异常值和定位误差时,(1)式完全成立;但实际中,检测算法得到的匹配点不仅包含异常值,还含有定位误差^[19],因此(1)式不完全成立。

图 1. 对极几何

Fig. 1. Epipolar geometry

下载图片查看所有图片

2.2 基础矩阵求解

设图像I中有n个匹配点m=(x,y,1)^T,图像Ⅱ中有n个匹配点m'=(x',y',1)与之对应,令 $\begin{matrix} F = [\begin{matrix} f_{1} & f_{2} & f_{3} \\ f_{4} & f_{5} & f_{6} \\ f_{7} & f_{8} & f_{9} \end{matrix}], 且将 F 记为 f = {[\begin{matrix} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} & f_{6} & f_{7} & f_{8} & f_{9} \end{matrix}]}^{T} 。 \end{matrix}$ 由(1)式和n个匹配点可得n个方程:

\begin{matrix} Af = [\begin{matrix} x_{1} x'_{1} & x_{1} y'_{1} & x_{1} & x'_{1} y_{1} & y_{1} y'_{1} & y_{1} & x'_{1} & y'_{1} & 1 \\ ︙ & ︙ & ︙ & ︙ & ︙ & ︙ & ︙ & ︙ & ︙ \\ x_{n} x'_{n} & x_{n} y'_{n} & x_{n} & x'_{n} y_{n} & y_{n} y'_{n} & y_{n} & x'_{n} & y'_{n} & 1 \end{matrix}] f = 0 。 (2) \end{matrix}

由(2)式可看出,如果该式存在精确(非零)解,则系数矩阵A的秩最多是8 。

3 改进的密度峰值快速聚类算法

3.1 聚类核心思想及不足

密度峰值算法核心思想为通过两个特征描述类中心进行数据聚类:1)类中心本身局部密度值较大;2)类中心与其他密度大的点的距离较远。其主要原理如下。

设聚类数据集为X= $\begin{matrix} \{x_{1}, x_{2}, \dots, x_{n}\} \end{matrix}$ ,计算数据点x_i的局部密度,局部密度ρ_i的定义如下。

1) 截断核

对于截断核,其局部密度的定义式为

\begin{matrix} ρ_{i} = \sum_{j} χ (d_{ij} - d_{c}), (3) \end{matrix}

式中:d_ij为数据点i与数据点j之间的距离;d_c为截断距离,且需人工指定。函数χ(a)为布尔型函数,定义式为

\begin{matrix} χ (a) = \{\begin{matrix} 1, & a < 0 \\ 0, & a \geq 0 \end{matrix}, (4) \end{matrix}

式中:a=d_ij-d_c,表示d_ij与截断距离d_c之间的差值。

2) 高斯核

对于高斯核,其局部密度的定义式为

\begin{matrix} ρ_{i} = \sum_{j} \exp [- {(\frac{d_{ij}}{d_{c}})}^{2}] 。 (5) \end{matrix}

由两个不同的局部密度计算方式可以看出,前者计算的是离散值,每个数据点的密度值非0即1;而后者则是连续值。相对于截断核,高斯核计算后产生重复的可能性更小,因此在文献[ 16]中使用高斯核函数计算局部密度。

每个数据点的相对距离定义式为

\begin{matrix} δ_{i} = \min_{j : ρ_{j} > ρ_{i}} (d_{ij}), (6) \end{matrix}

式中:d_ij为聚类算法输入,表示聚类数据点i与点j之间的距离,文中为匹配点到极线的距离。对于局部密度ρ_i最大的数据点x_i,其相对距离为δ_i= $\begin{matrix} \max_{j} \end{matrix}$ (d_ij)。由(6)式定义可知:当数据点x_i的局部密度ρ_i最大时,δ_i表示在整个数据集X中,x_i与距x_i离最远的点x_j之间的距离;否则,δ_i表示在所有局部密度大于x_i的点中,与x_i间距离最小的数据点与x_j之间的距离。

在基本密度峰值聚类算法中,仍有两个问题值得讨论和思考:1)计算局部密度时d_c的参数选取问题。通过实验发现,d_c的选取会影响数据点局部密度的计算,而数据点局部密度对聚类的结果起着决定性作用。 2)聚类中心选取问题。文献[ 16]中提到该算法可实现自动聚类的效果,但经过实验发现,聚类中心需要人为从聚类结果的距离-密度图(ρ-δ图,即决策图)中选取,而手动选取聚类中心具有很强的主观性,因此并未实现自动聚类。

3.2 改进密度峰值算法

针对基本密度峰值算法存在的不足,本文提出以下两点改进。

1) 改进局部密度

密度峰值算法利用高斯核计算数据点的局部密度,其中高斯核函数参数d_c需提前设定,但d_c的设定不合理将导致算法无法收敛或不能正确聚类:如果d_c取得过大,则将使每个数据的局部密度都很大以至于区分度不高,导致将所有数据点都归为一类;反之,则可能出现聚类中心数与数据点总数相同的情形,导致聚类失败。本文中虽然聚类数据中的距离数据为匹配点(含有误差的匹配点不在极线上)到极线的距离,即对极距离,但随着算法迭代次数增加,对极距离逐渐减小,出现较多零值,因此当d_c设置过大或过小(文献[ 16]设置d_c为1%~2%)时,密度峰值算法会失效。基于此,本文利用多核学习的优点,通过改进局部密度函数来提升算法性能。

设N为匹配点数目,Q为核函数数目,ρ'_i为改进后的局部密度,重新定义局部密度,定义式为

\begin{matrix} ρ'_{i} = \overset{N}{\sum_{j}} \overset{Q}{\sum_{q = 1}} α_{q} k (d_{ij}, σ_{q}, r_{q}), (7) \end{matrix}

式中: $\begin{matrix} k (d_{ij}, σ_{q}, r_{q}) = \exp [- d_{ij}^{2} / (r_{q} \cdot σ_{q}^{2})] 为高斯核函数; \end{matrix}$ σ_q为第q个核函数的尺度因子;r_q为第q个核函数尺度因子系数;α_q为第q个核函数权值。

将高斯核函数尺度化后可得到一系列不同尺度的高斯核函数,且满足σ₁<σ₂<…<σ_q。根据小波变化理论中尺度变化规律,将尺度因子定义为

\begin{matrix} σ_{q} = 2^{q} σ, q = 1,2, \dots, Q, (8) \end{matrix}

式中:σ=d_c;Q为q的最大值。当Q为有限值时,多核学习为有限核学习方式;当Q趋近于无穷大时,则称这种多核学习方式为无限核学习方法。相对于基于智能优化算法和基于神经网络的方法,利用实验法确定核函数数目较为简单实用。本文使用实验法确定核函数数目,每增加一个核函数,平均对极距离的精度将提高一个数量级(若核函数数目为3,则平均对极距离精度为10^-3)。由于文献[ 1-2,7-9]等均以10^-4精度为前提,且随着平均对极距离精度的增加,不仅计算量上升,而且计算时间也将增加,所以本文取平均对极距离的精度为10^-4,从而高斯核函数数目Q取4。

多核学习中权值决定着整个算法的优劣,本文使用多核学习中的序列学习方法对多尺度高斯核函数权值进行学习。序列学习法确定权值步骤如下:根据原始数据大小确定权值初始值,而大尺度核权值起主导作用,一般在0.5~0.95之间变化,若原始数据较大(数据个数超过10000)则初始化为0.5,若较小则初始化为0.95。文中原始数据(即图像特征点)个数为200~2500不等,相对于文献[ 13]原始数据取值范围为1000~10000,本文数据量较小且聚类数目较小,基本可分为三类,即内点、外点以及噪声数据(文献[ 13]中聚类数为2~14不等)。因此将大核权值初始化为0.95,然后,以初始值为起点,步长λ=0.01,将α₁逐次递减至0.5,相应的α₂逐次递增,其余权值α₃~α_q保持不变;计算每次聚类误差并与上一次误差比较,得到其中最小误差对应的最佳权值α₁;此时固定α₁,以当前的α₂为初始值,步长λ为0.01,将α₂逐次递减至0.01(核函数的最小权值),相应的α₃逐次递增,其余权值α₄~α_q保持不变,计算每次聚类误差并与上一次误差比较,得到其中最小误差对应的最佳权值α₂和α₃(若没有最小误差,则初始值为最佳权值),依次确定剩余权值,直到所有权值确定完毕,则得到了每个核函数的最佳权值。

将基本密度峰值聚类与改进后的多核学习-密度峰值聚类对比,分类数据使用文献[ 16]中的数据,结果如图2、3所示。图2(b)横纵坐标表示文献[ 16]原始数据的横纵坐标。基本密度峰值算法选择实验中较好的一次实验结果,阈值d_c=1.8。是否应将图2中箭头所指虚线圆圈中的点判断为聚类中心是一个重要的问题:如果将它划分为聚类中心,则聚类会出现错误,导致聚类失败。从图2(b)可以发现,即使阈值选择最优值,图中右上角虚线矩形框内的类别依然会将很多离群点聚为一类,因此基本密度峰值算法存在一定的不足。本文通过使用多核学习的方法,构造了多尺度的高斯核函数,使用权值系数分配不同尺度核函数所占比例,使得聚类效果达到最佳。由图3可以直观看到,5个聚类中心位置较其他数据点更加明显,很容易选出聚类中心,同时,聚类结果较基本密度峰值算法更好。

图 2. 基本密度峰值算法的结果(d_c=1.8)。(a)决策图;(b)聚类结果

Fig. 2. Experimental results of basic density peak algorithm(d_c=1.8). (a) Decision graph; (b) clustering results

下载图片查看所有图片

图 3. 多核学习-密度峰值算法的结果。(a)决策图;(b)聚类结果

Fig. 3. Experimental results of multi-kernel learning-density peak algorithm. (a) Decision graph; (b) clustering results

下载图片查看所有图片

2) 改进聚类中心选取方式

实现聚类自动化不仅能加快算法执行效率,同时还能够提高聚类的准确性。但当某几类数据密度较接近时,无法精确选取聚类中心且人为选取主观性较强^[20],本文通过分析局部密度与距离的关系发现,聚类中心的密度值较大,且与其他密度较小的数据点间的距离也较大,分布于决策图的上半部分(如图2、3所示)或不同于其他数据点,因此可定义如下聚类中心判别式以实现自动聚类:

\begin{matrix} γ_{i} = \sqrt[]{ρ'_{i} \cdot δ_{i}}, (9) \end{matrix}

式中:ρ'_i为改进的局部密度;δ_i为相对距离。局部密度较大的点使γ_i更大,相反,γ_i值越小。显然,如果γ_i越大,则该点可能为聚类中心。此时,只需对γ_i进行降序排列并作γ_i的分布图,如图4所示,通过选取阈值(图中的红分割线)即可自动选择聚类中心。

图 4. γ分布图

Fig. 4. Distribution map of γ

下载图片查看所有图片

4 多核学习-密度峰值算法的基础矩阵估计

可以将基础矩阵的估计看作聚类问题,即将匹配点聚为两大类:内点集和外点集。外点集由特征匹配时的误匹配特征点组成,误差较大,因此需要剔除;而内点集包含正确匹配点,且理论上不含误差。如果内点集没有定位误差,且和外点严格分离,那么用此内点集估计基础矩阵,将能有效提高基础矩阵的估计精度和准确性。因此,选择一个较优的聚类算法,有益于有效地提高基础矩阵估计精度。

4.1 基础矩阵估计原理

根据(3)式得到n个方程,利用最小二乘法找到一组满足方程的精确解,即得到基础矩阵中每个元素。线性求解基础矩阵,利用最小二乘法解方程组,求解过程简单,速度较快,是求解初始基础矩阵较为实用的方法。本文首先使用归一化八点算法^[21]计算初始基础矩阵,它能够在匹配点无异常值与定位误差时,较为精确地计算基础矩阵,因此被广泛应用。其计算过程如下: 1)由平移变换矩阵T和伸缩变换矩阵T'对每个数据点进行归一化处理;2)求解对应点的基础矩阵,包括求线性解和奇异值分解(SVD);3)解除归一化。

为了避免随机选择匹配点导致的初始基础矩阵误差较大的问题,本文基于抽样思想^[4]提出随机分块抽样法,通过随机分块抽样法选取8对匹配点以此计算初始矩阵,提高初始矩阵精度,具体方法如下。

计算匹配点中横、纵坐标最大与最小的点,记为X_max、X_min、Y_max、Y_min;将x轴等分成p个小栅格,p=X_max-X_min,删除没有匹配点的栅格,剩余p'个栅格,p'≤p;每次随机选择8个小栅格,并从中选取1个匹配点,由8点法计算基础矩阵;经过k次迭代后,得到k个基础矩阵,记为F_e(e=1,…,k),计算每个F_e的二范数,并将其降序排列,取其中最大的矩阵二范数对应的F_e作为初始基础矩阵,记为F_{inital_opt}。

图 5. 栅格划分示意图

Fig. 5. Raster division diagram

下载图片查看所有图片

由于基础矩阵估计中损失函数的不同,估计误差的描述也有所不同。基础矩阵计算中,余差能够直接反映基础矩阵的优劣,而对极距离描述了匹配点到相应极线的几何距离,它能够真实地反映出基础矩阵估计是否准确^[22]。为了使聚类结果更加准确,本文选用对极距离进行聚类,选用平均对极距离和余差来衡量不同算法的性能。余差的定义式为

\begin{matrix} r_{i} = |m'_{i} F m_{i}|, (10) \end{matrix}

对极距离的定义式为

\begin{matrix} \begin{matrix} d_{i} = d (m'_{i}, F m_{i}) + d (m_{i}, F^{T} m'_{i}) = \\ \{\frac{1}{{[(F m_{i})_{1}^{2} + (F m_{i})_{2}^{2}]}^{2}} + \frac{1}{{[(F^{T} m'_{i})_{1}^{2} + (F^{T} m'_{i})_{2}^{2}]}^{2}}\} |m'_{i} F m_{i}|, (11) \end{matrix} \end{matrix}

式中:(m_i,m'_i)表示第i对匹配点;Fm_i,F^Tm'_i分别表示匹配点m'_i与m_i对应的极线; $\begin{matrix} d (m'_{i}, F m_{i}), d (m_{i}, Fm'_{i}) 表示两幅图中匹配点 m'_{i} 与 m_{i} 到各自极线的距离; (F m_{i})_{v}^{2} 为 F m_{i} 的第 v 个分量, v = 1, \end{matrix}$ 2。

平均对极距离的定义式为

\begin{matrix} \bar{D} = \overset{N}{\sum_{i = 1}} d_{i} / N, (12) \end{matrix}

式中:d_i为第i个数据点的对极距离;N为匹配点总数目。

初始化基础矩阵F_{inital_opt}后,由对极距离(11)式计算匹配点x_i所对应的对极距离,得到聚类数据X。利用3.2节中的多核学习-密度峰值聚类算法对数据点进行聚类,算法步骤如下。

步骤1:设置初始权值α₁=1,α₂、α₃、α₄=0,并用x=(x-x_min)/(x_max-x_min)(其中x_min为聚类数据的最小值,x_max为最大值)归一化聚类数据X。

步骤2:按照(7)式计算所有数据点密度ρ'_i,并对密度值降序排列得到降序排列的下标序列。

步骤3:由(6)式计算数据点与其他数据点间的距离δ_i。

步骤4:由决策图和γ分布图自动选取聚类中心。

步骤5:对非聚类中心数据归类,并将其分为类中心数据与类边缘数据。

步骤6:标识聚类数据和异常值,判断平均对极距离是否达到精度阈值T_accuracy=10^-4,满足则算法结束,否则剔除异常值,回到步骤2)重新计算。

由多核学习-密度峰值算法剔除大量异常值得到较优候选内点集,使用M估计法最小化候选内点集中数据的余差以去除定位误差,重复以上步骤,当前一次平均对极距离运行结果和后一次平均对极距离的差值的绝对值小于精度阈值T_accuracy=10^-4或最大迭代次数达到T_iter=50(经过100次测试,本文算法在迭代30~50次时即可达到精度要求,因此最大迭代次数T_iter设置为50)时停止,得到最优内点子集,并计算最终的基础矩阵F_{inital_opt},F_{inital_opt}表示计算基础矩阵最终得到的最优结果。

4.2 基础矩阵估计流程图

基于多核学习-密度峰值算法的基础矩阵估计流程如图6所示。首先,使用随机分块抽样法和归一化8点法计算初始基础矩阵,当初始矩阵满足一定精度时,得到最佳初始矩阵并由对极距离(11)式计算每个数据点的对极距离得到聚类数据;其次,由多核学习-密度峰值算法对对极距离进行聚类,并剔除数据点中的异常数据;最后,使用M估计法除去匹配集中的定位误差得出最优内点子集,以此估计基础矩阵,若满足精度要求则对最终的基础矩阵进行奇异值分解得到最佳基础矩阵,否则返回第一步重新计算。

图 6. 基础矩阵估计流程图

Fig. 6. Flow chart of basic matrix estimation

下载图片查看所有图片

5 实验及分析

为验证本文算法的性能和有效性,使用模拟数据和真实图片进行实验,通过不同的误差衡量标准,将本文算法与LMedS、R-RANSAC、LO-RANSAC三种鲁棒估计方法进行比较,本实验使用的编程软件为matlab 2016b。

1) 模拟实验

在400×400×600的三维空间中产生100个随机点来模拟真实物体三维信息,将100个点投影到两个不同的平面,在两幅图中产生不同的匹配点。采取两种对比实验:①对两个不同平面的匹配点加入均值为零且方差不同的高斯噪声;②调整100对匹配点中匹配点位置,得到不同外点率的匹配点对。实验结果如图7和8所示。

由实验结果图7、8得出:①LMedS^[6]算法对噪声比较敏感,但对错误率在50%以下的异常值鲁棒性较好;相反,R-RANSAC算法对异常值鲁棒性较差,但对定位噪声较为鲁棒,验证了LMedS和R-RANSAC这两种算法的正确性;RO-RANSAC算法在外点率小于50%并且方差相对较小时性能较优。②当噪声方差σ=2并且外点率大于50%时,本文算法的平均对极距离均小于其他三种算法,验证了本文算法不仅在噪声较大时性能表现优异,而且对具有大量异常值的数据有较好的鲁棒性。③相对于其他三种算法,本文算法的平均对极距离最小,原因在于本文方法在最小化平均对极距离时,将异常值和有噪声的大量匹配点剔除,匹配内点集数目变小,使得基础矩阵计算更加精确。

表 1. 4种算法性能比较

Table 1. Comparison of four algorithms performance

Performanceindicator	Algorithm	Graffiti	Tree	UBC	Bike	Fruit	INRIA	Building	Snow-tree
Total numberof matchedpoints	SURF	847	2231	1216	700	289	345	576	264
Number of matchedpoints forestimatingfundamental matrix	LMedS	424	1116	608	350	146	173	288	132
	R-RANSAC	185	670	271	57	31	37	115	35
	LO-RANSAC	71	231	172	21	11	12	50	20
	Proposed	132	228	178	39	20	25	49	26
Averageresidualerror	LMedS	8.6621	1.3738	2.3153	3.6393	2.6101	1.8034	2.6650	1.6481
	R-RANSAC	7.2744	1.0493	1.2101	2.2466	1.0466	1.1632	3.9613	1.2221
	LO-RANSAC	1.3897	0.3008	0.8200	0.4927	0.2826	0.4519	0.1052	1.3596
	Proposed	1.0513	0.2538	0.7017	0.3859	0.2183	0.3972	0.0844	1.1466
Averageepipolardistance /pixel	LMedS	0.3809	0.2466	0.3586	0.3651	0.2981	0.3152	0.3985	0.6759
	R-RANSAC	0.1511	0.1362	0.1461	0.1712	0.1026	0.1481	0.1324	0.1192
	LO-RANSAC	0.0588	0.0961	0.0781	0.0902	0.0718	0.0660	0.0752	0.0956
	Proposed	0.0414	0.0830	0.0691	0.0782	0.0673	0.0592	0.0644	0.0868
Computationaltime /s	LMedS	0.1481	0.2176	0.2817	0.1774	0.1053	0.1228	0.1736	0.1378
	R-RANSAC	0.1659	0.2351	0.4160	0.1405	0.0812	0.1369	0.1693	0.1596
	LO-RANSAC	0.1302	0.1770	0.0906	0.1235	0.0443	0.1043	0.1396	0.1206
	Proposed	0.1493	0.2060	0.0975	0.1029	0.0427	0.0871	0.0906	0.1415

查看所有表

2)不同真实场景图片实验

本文使用加速稳健特征(SURF)图像匹配算法生成一系列匹配点,作为实验的原始数据。实验所用图片样本如图9所示,其中图9 (a)~(f)取自INRIA-DATASET标准图像匹配数据集,图9(g)、(h)取自不同真实场景。

图 7. 不同高斯方差噪声下4种方法的平均对极距离

Fig. 7. Average epipolar distance of four methods under different Gaussian variance noise

下载图片查看所有图片

图 8. 不同外点率下4种方法的平均对极距离

Fig. 8. Average epipolar distance of four methods at different external point rates

下载图片查看所有图片

图 9. 实验图片。(a)涂鸦;(b)阳光树;(c)哥伦比亚大学;(d)自行车;(e)水果;(f)研究所;(g)建筑;(h)雪树

Fig. 9. Experimental images. (a) Graffiti; (b) tree; (c) UBC; (d) bike; (e) fruit; (f) INRIA;(g) building; (h) snow-tree

下载图片查看所有图片

表1分别列出了每种场景下不同算法计算获得的最终匹配点数、余差、平均对极距离和计算时间。由表1可以看出: 1)对于最终估计基础矩阵所保留的匹配点数,LMedS方法最多,R-RANSAC法次之,本文算法与LO-RANSAC算法相当; 2)在误差和余差方面,相对于精度最高的LO-RANSAC算法,本文算法的余差和误差分别提高了16%和13%,证明了本文算法的精度和有效性较好; 3)从算法时间看,对于不同的场景图片,本文算法整体与其他算法相当,虽然计算时间出现时大时小的问题,但总体依然较小,原因是本文算法在聚类时,是根据不同的平均对极距离进行聚类,聚类次数由对极距离决定,因此当对极距离相差较大时,聚类次数增加,导致算法整体时间增加。

6 结论

本文提出一种多核学习-密度峰值聚类的鲁棒基础矩阵估计方法。以匹配点对极距离为特征,利用多核学习-密度峰值算法简单、快速的特点有效地剔除了异常值,并获得一个精度较高的候选内点集,使用M估计法去除候选内点集中的定位噪声得到最终的最佳内点子集,并使用最佳内点子集估计基础矩阵。与其他算法相比,在保证匹配点较多的前提下,本文算法能有效减小基础矩阵的估计误差,提高了基础矩阵估计精度和准确性。

参考文献

[1] 张永祥, 古佩强, 穆铁英. 改进的RANSAC基础矩阵估计算法[J]. 小型微型计算机系统, 2016, 37(9): 2084-2087.

Zhang Y X, Gu P Q, Mu T Y. Improved RANSAC algorithm for fundamental matrix estimation[J]. Journal of Chinese Computer Systems, 2016, 37(9): 2084-2087.

[2] 黄以君, 刘伟军. 基于LQS的基本矩阵计算方法[J]. 中国图象图形学报, 2009, 14(10): 2069-2073.

Huang Y Z, Liu W J. A method for fundamental matrix estimation using LQS[J]. Journal of Image and Graphics, 2009, 14(10): 2069-2073.

[3] 薛俊诗, 舒奇泉, 郭宁博. 未知畸变参数时多视图三维重建相对位姿估计方法[J]. 光子学报, 2018, 47(6): 0612002.

Xue J S, Shu Q Q, Guo N B. Relative pose estimation method in multi-view 3D reconstruction with unknown distortion[J]. Acta Photonica Sinica, 2018, 47(6): 0612002.

[4] TaiC, Liu YH. Robust structure and motion estimation by auto-scale random sample consensus[C]∥2006 IEEE International Conference on Information Acquisition, August 20-23, 2006, Weihai, China. New York: IEEE, 2006: 37- 42.

[5] Zou Y X, Chan S C, Ng T S. Least mean M-estimate algorithms for robust adaptive filtering in impulse noise[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2000, 47(12): 1564-1569.

[6] Rousseeuw P J. Least median of squares regression[J]. Journal of the American Statistical Association, 1984, 79(388): 871-880.

[7] 王琼, 李言, 任伟建, 等. 图像三维重构中基于混合算法的基础矩阵估计[J]. 自动化技术与应用, 2017, 36(7): 1-6, 12.

Wang Q, Li Y, Ren W J, et al. Fundamental matrix estimation based on improved hybrid algorithm in image 3D reconstruction[J]. Techniques of Automation and Applications, 2017, 36(7): 1-6, 12.

[8] 颜坤, 刘恩海, 赵汝进, 等. 快速鲁棒的基础矩阵估计[J]. 光学精密工程, 2018, 26(2): 461-470.

Yan K, Liu E H, Zhao R J, et al. A fast and robust method for fundamental matrix estimation[J]. Optics and Precision Engineering, 2018, 26(2): 461-470.

[9] 鲁珊, 雷英杰, 孔韦韦, 等. 基于模糊核聚类的鲁棒性基础矩阵估计算法[J]. 吉林大学学报(工学版), 2012, 42(2): 434-439.

Lu S, Lei Y J, Kong W W, et al. Robust fundamental matrix estimation based on kernel fuzzy clustering[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(2): 434-439.

[10] Chum O, Matas J. Optimal randomized RANSAC[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(8): 1472-1482.

[11] ChumO, MatasJ, KittlerJ. Local lyoptimized RANSAC[M] ∥Michaelis B, Krell G. Pattern recognition. DAGM 2003. Lecture notes in computer science. Berlin, Heidelberg: Springer, 2003, 2781: 236- 243.

[12] 董安国, 李佳逊, 张蓓, 等. 基于谱聚类和稀疏表示的高光谱图像分类算法[J]. 光学学报, 2017, 37(8): 0828005.

Dong A G, Li J X, Zhang B, et al. Hyperspectral image classification algorithm based on spectral clustering and sparse representation[J]. Acta Optica Sinica, 2017, 37(8): 0828005.

[13] 周世波, 徐维祥. 一种基于相对密度和决策图的聚类算法[J]. 控制与决策, 2018, 33(11): 1921-1930.

Zhou S B, Xu W X. A novel clustering algorithm based on relative density and decision graph[J]. Control and Decision, 2018, 33(11): 1921-1930.

[14] 曾台英, 杜菲. 基于层次聚类的图像超分辨率重建[J]. 光学学报, 2018, 38(4): 0410004.

Zeng T Y, Du F. Image super-resolution reconstruction based on hierarchical clustering[J]. Acta Optica Sinica, 2018, 38(4): 0410004.

[15] 赵凯, 徐友春, 李永乐, 等. 基于VG-DBSCAN算法的大场景散乱点云去噪[J]. 光学学报, 2018, 38(10): 1028001.

Zhao K, Xu Y C, Li Y L, et al. Large-scale scattered point-cloud denoising based on VG-DBSCAN algorithm[J]. Acta Optica Sinica, 2018, 38(10): 1028001.

[16] Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.

[17] 韩利钊, 钱雪忠, 罗靖, 等. 基于区域划分的DBSCAN多密度聚类算法[J]. 计算机应用研究, 2018, 35(6): 1668-1671, 1685.

Han L Z, Qian X Z, Luo J, et al. Multi-density clustering algorithm DBSCAN based on region division[J]. Application Research of Computers, 2018, 35(6): 1668-1671, 1685.

[18] 李静, 杨宜民, 张学习. 一种改进的MLESAC基本矩阵估计算法[J]. 计算机工程, 2012, 38(19): 214-217.

Li J, Yang Y M, Zhang X X. Animproved MLESAC algorithm for estimating fundamental matrix[J]. Computer Engineering, 2012, 38(19): 214-217.

[19] 向长波, 刘太辉. 基本矩阵的鲁棒贪心估计算法[J]. 计算机辅助设计与图形学学报, 2007, 19(5): 651-655.

Xiang C B, Liu T H. A robust greedy algorithm for estimating the fundamental matrix[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(5): 651-655.

[20] 王洋, 张桂珠. 自动确定聚类中心的密度峰值算法[J]. 计算机工程与应用, 2018, 54(8): 137-142.

Wang Y, Zhang G Z. Automatically determine density of cluster center of peak algorithm[J]. Computer Engineering and Applications, 2018, 54(8): 137-142.

[21] Hartley R I. In defense of the eight-point algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593.

[22] 李言. 基于未标定图像的油田地面设备三维重建研究与实现[D]. 大庆: 东北石油大学, 2016.

LiY. Research and implementation on 3D reconstruction about oilfield ground equipment of uncalibrated image[D]. Daqing: Northeast Petroleum University, 2016.

王剑峰, 王宏伟, 闫学勤. 基于多核学习-密度峰值聚类的基础矩阵估计[J]. 激光与光电子学进展, 2020, 57(4): 041017. Jianfeng Wang, Hongwei Wang, Xueqin Yan. Fundamental Matrix Estimation Based on Multiple Kernel Learning-Density Peak Clustering[J]. Laser & Optoelectronics Progress, 2020, 57(4): 041017.

基于多核学习-密度峰值聚类的基础矩阵估计下载： 797次

1 引言

2 对极几何及基础矩阵

2.1 对极几何

图 1. 对极几何

Fig. 1. Epipolar geometry

2.2 基础矩阵求解

3 改进的密度峰值快速聚类算法

3.1 聚类核心思想及不足

3.2 改进密度峰值算法

图 2. 基本密度峰值算法的结果(d_c=1.8)。(a)决策图;(b)聚类结果

Fig. 2. Experimental results of basic density peak algorithm(d_c=1.8). (a) Decision graph; (b) clustering results

图 3. 多核学习-密度峰值算法的结果。(a)决策图;(b)聚类结果

Fig. 3. Experimental results of multi-kernel learning-density peak algorithm. (a) Decision graph; (b) clustering results

图 4. γ分布图

Fig. 4. Distribution map of γ

4 多核学习-密度峰值算法的基础矩阵估计

4.1 基础矩阵估计原理

图 5. 栅格划分示意图

Fig. 5. Raster division diagram

4.2 基础矩阵估计流程图

图 6. 基础矩阵估计流程图

Fig. 6. Flow chart of basic matrix estimation

5 实验及分析

表 1. 4种算法性能比较

Table 1. Comparison of four algorithms performance

图 7. 不同高斯方差噪声下4种方法的平均对极距离

Fig. 7. Average epipolar distance of four methods under different Gaussian variance noise

图 8. 不同外点率下4种方法的平均对极距离

Fig. 8. Average epipolar distance of four methods at different external point rates

图 9. 实验图片。(a)涂鸦;(b)阳光树;(c)哥伦比亚大学;(d)自行车;(e)水果;(f)研究所;(g)建筑;(h)雪树

Fig. 9. Experimental images. (a) Graffiti; (b) tree; (c) UBC; (d) bike; (e) fruit; (f) INRIA;(g) building; (h) snow-tree

6 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

基于多核学习-密度峰值聚类的基础矩阵估计 下载： 797次

1 引言

2 对极几何及基础矩阵

2.1 对极几何

图 1. 对极几何

Fig. 1. Epipolar geometry

2.2 基础矩阵求解

3 改进的密度峰值快速聚类算法

3.1 聚类核心思想及不足

3.2 改进密度峰值算法

图 2. 基本密度峰值算法的结果(dc=1.8)。(a)决策图;(b)聚类结果

Fig. 2. Experimental results of basic density peak algorithm(dc=1.8). (a) Decision graph; (b) clustering results

图 3. 多核学习-密度峰值算法的结果。(a)决策图;(b)聚类结果

Fig. 3. Experimental results of multi-kernel learning-density peak algorithm. (a) Decision graph; (b) clustering results

图 4. γ分布图

Fig. 4. Distribution map of γ

4 多核学习-密度峰值算法的基础矩阵估计

4.1 基础矩阵估计原理

图 5. 栅格划分示意图

Fig. 5. Raster division diagram

4.2 基础矩阵估计流程图

图 6. 基础矩阵估计流程图

Fig. 6. Flow chart of basic matrix estimation

5 实验及分析

表 1. 4种算法性能比较

Table 1. Comparison of four algorithms performance

图 7. 不同高斯方差噪声下4种方法的平均对极距离

Fig. 7. Average epipolar distance of four methods under different Gaussian variance noise

图 8. 不同外点率下4种方法的平均对极距离

Fig. 8. Average epipolar distance of four methods at different external point rates

图 9. 实验图片。(a)涂鸦;(b)阳光树;(c)哥伦比亚大学;(d)自行车;(e)水果;(f)研究所;(g)建筑;(h)雪树

Fig. 9. Experimental images. (a) Graffiti; (b) tree; (c) UBC; (d) bike; (e) fruit; (f) INRIA;(g) building; (h) snow-tree

6 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于多核学习-密度峰值聚类的基础矩阵估计下载： 797次

图 2. 基本密度峰值算法的结果(d_c=1.8)。(a)决策图;(b)聚类结果

Fig. 2. Experimental results of basic density peak algorithm(d_c=1.8). (a) Decision graph; (b) clustering results