基于自动编码器的光学图像加密方法

鲍震杰; 薛茹

doi:doi:10.3788/LOP202158.2210011

激光与光电子学进展, 2021, 58 (22): 2210011, 网络出版: 2021-11-05

基于自动编码器的光学图像加密方法下载： 1037次

Optical Image Encryption Method Based on Autoencoder

论文大纲

鲍震杰薛茹 ^*

作者单位

西藏民族大学信息工程学院, 陕西咸阳 712082

School of Information Engineering, Xizang Minzu University, Xianyang, Shaanxi 712082, China

AI词云图 AI语音精读 AI语音超短摘要

注：本部分内容由 AI 自动生成，仅供您参考。对于您使用本站 AI 自动生成内容所产生的一切后果，本网站及平台运营方概不承担任何商业和法律责任，请您知悉。

摘要

为了保护图像隐私、解决光学图像加密对光学仪器精密度依赖度高的问题,提出了基于自动编码器的光学图像加密方法。该方法使用深度神经网络模拟双随机相位编码,通过在输入中加入目标随机图像模仿第一层随机相位模板,利用编码网络的卷积核模仿第二层随机相位模板。卫星图像实验结果表明,本文方法能有效地加密光学图像,直方图上密文图像像素点分布较为均匀。和基于CycleGAN的加密方法相比较,本文方法更简单,计算资源消耗更少,加密性能不受光学仪器性能的影响,加密后图像的峰值信噪比(PSNR)值下降了6.5745,水平、垂直和对角方向上相邻像素的相关系数绝对值分别低了0.110375,0.118625,0.01335,解密后图像的PSNR值上升了1.4075,结构相似性值高了0.0428。

Abstract

In order to protect the image privacy and solve the problem that optical image encryption relies on high precision of optical instrument, an optical image encryption method based on an autoencoder is proposed. In this method, a deep neural network is used to simulate double random phase encoding. The target random image added into the input is used for simulating the first random phase template, and the convolution kernel of the encoding network is used for simulating the second layer random phase template. The experimental results of satellite images show that this method can effectively encrypt optical images, and the pixel distribution of ciphertext images on histograms is relatively uniform. Compared with the encryption method based on CycleGAN, this method is simpler and consumes less computing resources. The peak signal-to-noise ratio (PSNR)value of the encrypted image decreases by 6.5745, and the absolute values of the correlation coefficients of adjacent pixels in the horizontal, vertical, and diagonal directions decrease by0.110375, 0.118625, and0.01335, respectively. The PSNR value of the decrypted image increases by 1.4075, and the structural similarity value increases by 0.0428.

1 引言

近年来,信息网络的高速发展在给人们带来便利的同时,也带来了个人信息隐私的安全问题。图像加密能有效地提高图像传输的安全性,隐藏图像的原有信息,让没有解密手段的人看到的图像是毫无意义的。图像光学加密手段是图像加密的一种重要方法。结合矢量分解和相位剪切,文献[ 1]提出一种非对称光学图像加密算法。文献[ 2]提出了基于混沌Gyrator变换与离散小波变换的多图像光学同步加密算法。

基于光学图像的双随机相位编码,许多不同的学者和研究人员提出了很多加密方法。文献[ 3]提出了一种Logistic-Logistic级联混沌与矢量分解的无损压缩光学图像加密方法。基于多模光纤散斑的压缩感知,结合双随机相位编码,文献[ 4]提出了一种光学图像加密方法。文献[ 5]提出了基于空间角度复用和双随机相位的多图像光学加密方法。

深度学习在图像处理领域得到广泛应用,基于深度学习的方法为解决图像加密的问题提供了新的思路。文献[ 6]使用神经网络生成了置乱图像,并且通过训练自适应网络来识别置乱图像的原始类别。文献[ 7]使用CycleGAN网络直接对医学图像进行加密和解密,并提出了感兴趣区域的挖掘网络,直接从加密的图像中提取感兴趣的对象。

为将光学图像加密和深度学习有机融合,文献[ 8]采用经典双随机相位编码加密明文样本图案,构造明文图像-密文图像训练集以训练循环生成对抗网络(CycleGAN),并通过自动学习进行光学加密。

光学图像加密方法大都对光学仪器和材料的精度要求较高,为突破光学图像加密受光学器件性能的限制,本文通过设计自动编码器模拟对光学图像双随机相位编码的加密过程,使用深度神经网络模拟光学编码方式,通过在输入中加入目标产生的随机图像来模仿加密时的第一层随机相位模板,编码网络中的卷积核则用来模拟加密时的第二层随机相位模板。将明文图像和目标产生的随机图像经过编码网络,以生成均匀分布像素的随机图像,通过解码网络重塑原图像。

2 自动编码器

Hinton等^[9]描述的自动编码器是一种编码和重建模型,它使用一组识别权值将输入向量转换为隐藏向量,然后使用一组生成权值将隐藏向量转换为输入向量的近似重建量。自动编码器的深度学习模型广泛应用于文字表示^[10]、图像超分辨率^[11]、图像识别^[12]、语音识别^[13]、信号重建与分析^[14]等多媒体领域。

近年来,自动编码器也有新的应用。文献[ 15]提出了一种指纹特征提取方法,通常称为Fisher分数-堆叠稀疏自动编码器(Fisher-SSAE)方法,该方法消除了一些Fisher分数较低的特征,通过SSAE提取代表性特征。文献[ 16]提出了一种稀疏卷积自动编码器(CAE),用于在病理学组织图像中同时进行细胞核检测和特征提取。文献[ 17]提出了一种社区感知的动态网络嵌入(CDNE)方法,该方法采用了一种堆叠式深度自动编码的算法。

3 双随机相位编码

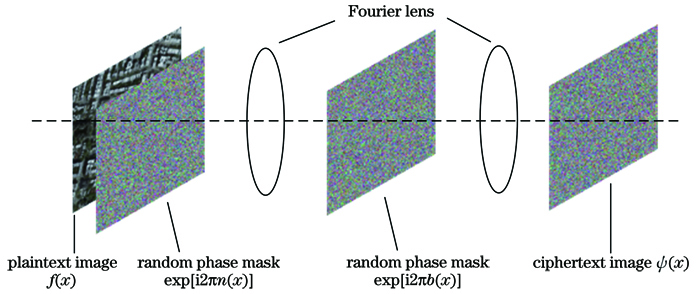
双随机相位编码架构如图1所示,假设f(x)是明文图像,ψ(x)是密文图像,n(x)和b(x)分别为两个在[0,1]范围内的相互独立的随机序列分布,则两个随机相位模板分别为exp[i2πn(x)]和exp[i2πb(x)],双随机相位编码的加密原理是:先将明文图像f(x)与随机相位模板exp[i2πn(x)]相乘,对得到的结果进行傅里叶变换FT{·},然后再与随机相位模板exp[i2πb(x)]进行卷积,最后通过傅里叶逆变换FT^-1{·}得到密文图像:

ψ (x) = F T^{- 1} {FT {f (x) \exp [i 2 π n (x)]} *exp [i 2 π b (x)]}, (1)

式中:*表示卷积。对于解密过程,首先对密文图像ψ(x)进行光学傅里叶变换,然后将所得结果与随机相位模板exp[-i2πb(x)]相乘,再进行傅里叶逆变换得到f(x)exp[i2πn(x)],在输出平面用CCD探测并记录f(x,y)^[18]。

图 1. 双随机相位编码架构

Fig. 1. Architecture of double random phase encoding

下载图片查看所有图片

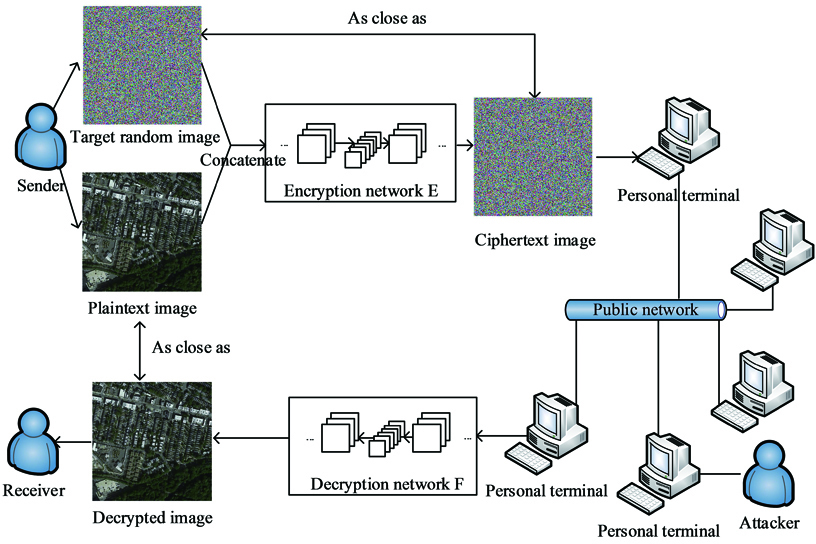
4 自动光学图像加密网络

如图2所示,自动光学图像加密网络由编码网络E、解码网络F构成,编码网络主要用于生成目标随机图像,解码网络则用于恢复原来的明文图像。

图 2. 自动光学图像加密网络的结构

Fig. 2. Structure of automatic optical image encryption network

下载图片查看所有图片

4.1 损失函数

假设x是明文图像且服从p_data(x)分布,则x~p_data(x);y是目标随机图像且服从p_data(y)分布,则y~p_data(y)。首先将明文图像x与目标随机图像y合并,编码网络E生成和目标随机图像y相似的密文图像E(x+y)。本文提出的编码损失函数为

\begin{array}{l} L_{encode} (E, F) = E_{x ~ p_{data} (x), y ~ p_{data} (y)} [{(E (x + y) - y)}_{2}] = E_{x ~ p_{data} (x), y ~ p_{data} (y)} \{{[E (x + y) - y]}^{2}\} = \\ E_{x ~ p_{data} (x), y ~ p_{data} (y)} \{\overset{n}{\sum_{i = 1}} {[E (x_{i} + y_{i}) - y_{i}]}^{2}\} = E_{x ~ p_{data} (x), y ~ p_{data} (y)} {{[E (x_{1} + y_{1}) - y_{1}]}^{2} + \dots + \\ {[E (x_{i} + y_{i}) - y_{i}]}^{2}}, (2) \end{array}

式中:x_i、y_i分别为一次迭代训练时的第i张明文图像和目标随机图像。

当输入密文图像时,编码网络有能力恢复原始的明文图像,因此,本文提出了解码损失函数:

\begin{array}{l} L_{decode} (E, F) = E_{x ~ p_{data} (x), y ~ p_{data} (y)} \{{(F [E (x + y)] - x)}_{2}\} = E_{x ~ p_{data} (x), y ~ p_{data} (y)} \{{\{F [E (x + y)] - x\}}^{2}\} = \\ E_{x ~ p_{data} (x), y ~ p_{data} (y)} \{\overset{n}{\sum_{i = 1}} {\{F [E (x_{i} + y_{i})] - x_{i}\}}^{2}\} = E_{x ~ p_{data} (x), y ~ p_{data} (y)} {{\{F [E (x_{1} + y_{1})] - x_{1}\}}^{2} + \dots + \\ {\{F [E (x_{i} + y_{i})] - x_{i}\}}^{2}} 。 (3) \end{array}

本文将编码损失函数和解码损失函数相加,得到了全局损失函数:

L_{full} (E, F) = L_{encode} (E, F) + λ L_{decode} (E, F), (4)

式中:λ为可调整参数。编码网络和解码网络的目标函数为

(E^{*}, F^{*}) = \arg \min_{F, E} L (E, F) 。 (5)

4.2 神经网络结构

本文编解码神经网络结构如图3所示,根据图像输入和输出的分辨率为256×256,本文的编解码神经网络结构借鉴CycleGAN模型^[19]和文献[ 20]。本文编码神经网络包括:一个卷积核为7×7、步长为1的卷积层,两个卷积核为3×3、步长为2的卷积层,以及9个残差块^[21]。残差块连接两个卷积核为3×3、步长为2的卷积层,每个卷积层后为Instancenormalization^[22]层,第一个卷积层的Instancenormalization层后还有ReLU激活函数,最后将残差块输入加上残差块输入经过两个卷积核为3×3、步长为2的卷积层后的输出之和经过ReLU激活函数输出。采用9个残差块之后的两个卷积核为3×3、步长为1/2的卷积层对特征映射进行上采样,每个降采样和上采样卷积层采用ReLU激活函数和Instancenormalization层,之后连接一个卷积核为7×7、步长为1的卷积层,再经Tanh激活函数处理。解码神经网络结构则与编码神经网络结构一致。

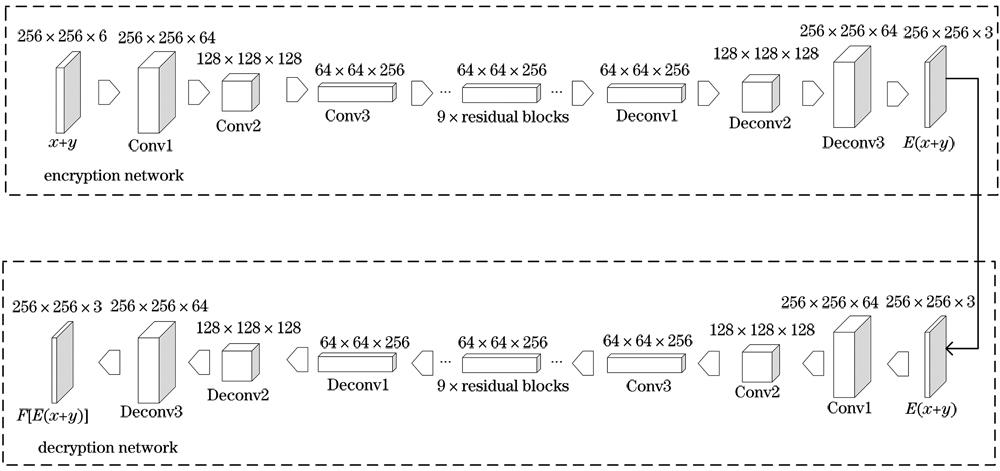
图 3. 自动光学图像加密网络的神经网络结构

Fig. 3. Neural network structure of automatic optical image encryption network

下载图片查看所有图片

4.3 模型训练和图像加解密过程

设W是卷积参数,W_n是第n个卷积层的参数,w_n_,_j是第n个卷积层的第j个参数,s_n×s_n是第n个卷积层的卷积核大小,c_input是输入通道数,c_output是输出通道数。对卷积层参数W_n和w_n_,_j进行随机初始化:

\begin{array}{l} W_{n} = random [w_{n, 1}, w_{n, 2}, \dots, w_{n, j}], (6) \\ w_{n, j} \leq sqrt (\frac{6}{s_{n} \times s_{n} \times c_{input} + s_{n} \times s_{n} \times c_{outpu t}}) 。 (7) \end{array}

将训练图像依次输入到深度学习模型中,由神经网络输出结果,根据损失函数计算误差,并将误差反向传递到整个神经网络的每个卷积层。为了获得更理想的输出结果,本文模型使用多次迭代学习,迭代采用梯度下降法以逐步减小误差,并对参数进行更新。编码网络和解码网络的梯度下降和模型参数更新过程可以表示为

\begin{array}{l} θ_{j} = θ_{j} - α \lor J (θ_{j}) = θ_{j} - α \frac{δ}{θ_{j}} J (θ_{j}) = θ_{j} - \frac{1}{m} α \frac{δ}{θ_{j}} \overset{m}{\sum_{i = 1}} {{[E (x_{i} + y_{i}) - y_{i}]}^{2} + \\ {F [E (x_{i} + y_{i})] - x_{i}}^{2}}, (8) \end{array}

式中:δ为偏导;θ_j是编码网络E或解码网络F的参数θ在第j次迭代时的值;α是学习率;∨J(θ_j)是参数θ_j对应方向上的梯度。模型训练完成后,对于加密过程,将256×256×3的明文图像和256×256×3的目标随机图像进行合并,生成一个新的矩阵,将像素值映射在[0,1]范围内,得到矩阵X⁰,然后将矩阵输入编码网络E。将训练好的第L层卷积核W^L与第L层输入矩阵X^L相应的元素相乘并通过相加得到下一层的输入元素 $X_{*}^{L + 1}$ ,滑动卷积核W^L将其与输入矩阵X^L下一组相应的元素相乘并将乘积相加,直至得到第L+1层的输入矩阵X^L⁺¹,重复以上操作,直至遍历所有神经网络层,将最后得到的输出X²⁴转化为密文图像。解密过程与加密过程类似。

5 实验结果与分析

5.1 实验环境

以卫星图像为训练和测试数据,实验中选用3242张分辨率为256×256的明文训练图像和50张明文测试图像,将图像像素值映射在[0,1]范围内。为了训练多样性,本文以50%概率对训练图像进行左右翻转,并对其使用改进的自动光学图像加密网络进行加密。自动光学图像加密网络的参数优化器选择Adam,初始学习率为0.0001。实验在Windows 10操作系统,GPU NVIDA GTX1060环境下运行。

5.2 模型收敛性

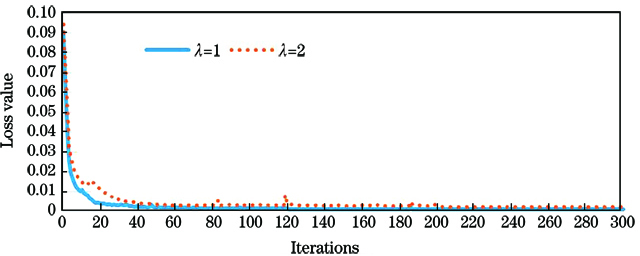
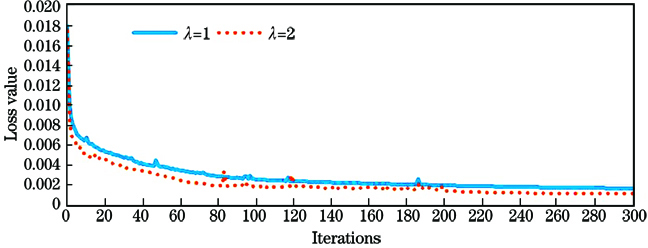
使用本文方法对训练图像进行训练,并记录模型编码损失[(1)式]和解码损失[(2)式]随着迭代次数增加的变化,绘制损失曲线(图4和图5)。图4纵坐标是损失值,横坐标是训练代数,虚线代表λ=2,实线代表λ=1。

图 4. 编码损失函数随迭代次数的变化

Fig. 4. Change of encoding loss function with iterations

下载图片查看所有图片

图 5. 解码损失函数随迭代次数的变化

Fig. 5. Change of decoding loss function with iterations

下载图片查看所有图片

从图4与图5可以看出,本文模型的编码损失值和解码损失值随着迭代次数的增加而不断下降,且下降至一个比较低的值,说明经过本文方法的加密,加密图像和随机图像差距小,解码后的图像也和原图像几乎一致,本文模型在训练中具有一定的稳定收敛性。λ=1时的编码损失值比λ=2时下降得更快且收敛值更低,而当λ=2时的解码损失值比λ=1时下降得更快且收敛值更低。为了得到更好的解密效果,本文设置λ=2。

5.3 实验结果

本文选择了4幅不同的彩色图片[图6(a)],采用本文方法进行加密[图6(b)],然后用本文方法进行解密[图6(c)]。

图 6. 自动光学图像加密网络的加密解密效果。(a)原始图像;(b)加密图像;(c)解密图像

Fig. 6. Encryption and decryption effects of automatic optical image encryption network。(a) Original images;(b) encryption images; (c) decryption images

下载图片查看所有图片

从图6可以看出:利用本文方法进行加密后,可隐藏原始图像信息,利用解密图像能恢复原图像信息,本文方法具有较好的视觉加密解密效果。

5.4 抗统计攻击分析

5.4.1 直方图分析

图7(a)为明文图像直方图,图7(b)为采用本文方法加密后的图像直方图,图7(c)为采用本文方法解密后的图像直方图。图7中横坐标为像素值,纵坐标为像素值的个数。

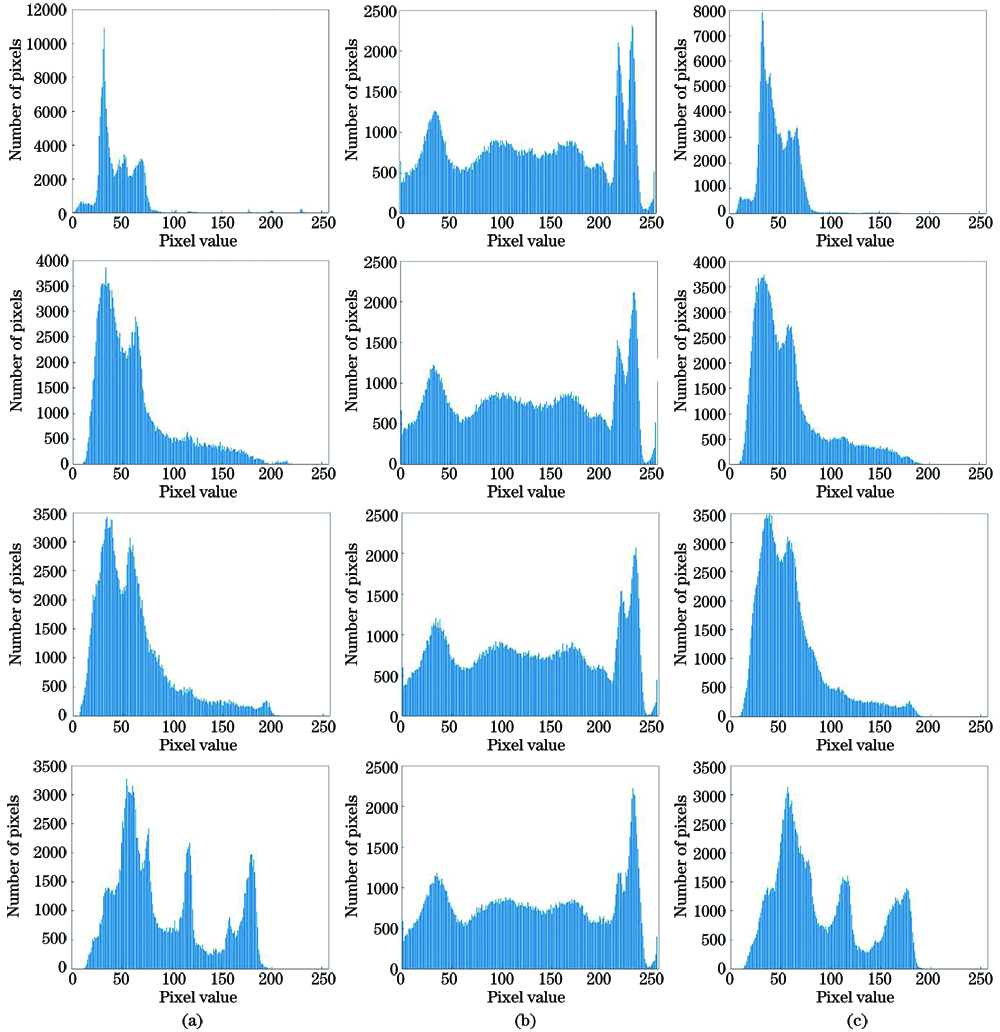
图 7. 自动光学图像加密网络的明文图像、加密图像与解密图像的直方图。(a)明文图像;(b)加密图像;(c)解密图像

Fig. 7. Histograms of plaintext images, encrypted images, and decrypted images in automatic optical image encryption network. (a) Plaintext images; (b) encrypted images; (c) decrypted images

下载图片查看所有图片

从图7可以看出,采用本文方法加密后的图像直方图与相应的明文图像直方图差距大,而采用本文方法解密后的图像直方图与明文图像直方图很相似。

5.4.2 相关性分析

由于明文图像的相邻像素之间存在很高的相关性,考虑到图像的安全性,加密图像相邻像素的相关性要足够小。设x和y是图像两个相邻像素的灰度值,N是选择的相邻像素对的个数。本文从明文图像和相应密文图像的垂直方向、水平方向和对角方向上随机选择4000对相邻像素, 计算x的期望E(x)、方差D(x),以及x、y的协方差cov(x,y)和相关系数 ${r_{x, y}}^{[23]}$ :

\begin{array}{l} E (x) = \frac{1}{N} \overset{N}{\sum_{i = 1}} x_{i}, (9) \\ D (x) = \frac{1}{N} \overset{N}{\sum_{i = 1}} {[x_{i} - Ε (x)]}^{2}, (10) \\ cov (x, y) = \frac{1}{N} \overset{N}{\sum_{i = 1}} \{[x_{i} ⁃ E (x)] [y_{i} - E (y)]\}, (11) \\ r_{x, y} = \frac{cov (x, y)}{\sqrt[]{D (x)} \sqrt[]{D (y)}} 。 (12) \end{array}

相关系数r_x_,_y越接近于0,说明图像相邻像素的相关性越低。

以图像(x,y)位置的像素值为纵坐标,分别以图像(x+1,y)、(x,y+1)和(x+1,y+1)位置的像素值为横坐标绘图,分析图像水平、垂直和对角方向上的像素相关度。图8(a)、(c)、(e)分别表示明文图像的水平、垂直和对角方向上的相关度,图8(b)、(d)、(f)分别表示密文图像的水平、垂直和对角方向上的相关度。从图8可以看出,明文图像散点图中的点分布集中,而经本文方法加密后图像散点图中的点分布较均匀,表示相邻像素间相关性更低。表1为密文图像水平、垂直和对角方向上的相关系数比较。

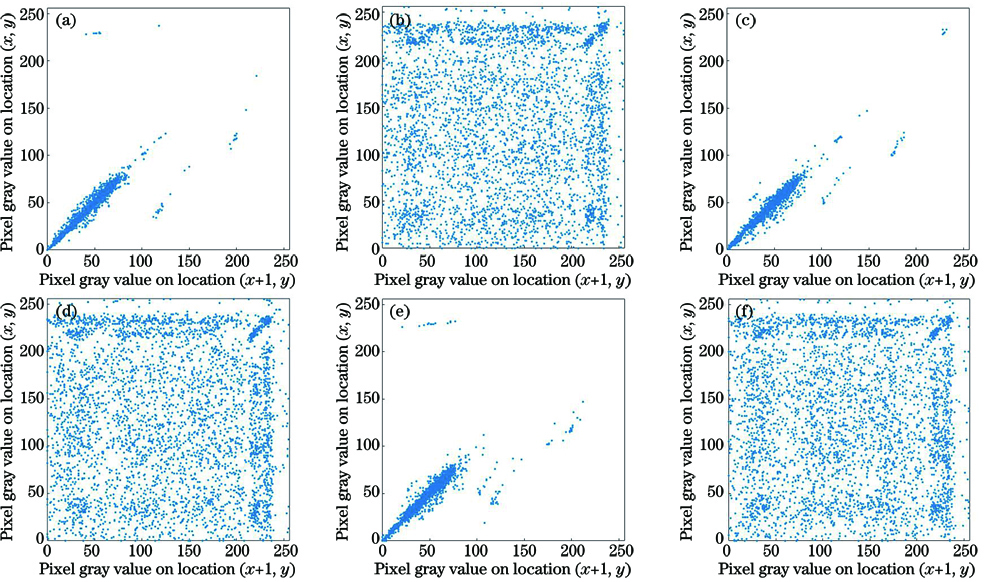
图 8. 明文图像与密文图像的水平、垂直和对角方向上的相邻像素散点图。(a)(b)水平方向;(c)(d)垂直方向;(e)(f)对角方向

Fig. 8. Scatter plots of adjacent pixels in horizontal, vertical, and diagonal directions of plaintext image and ciphertext image. (a)(b) Horizontal direction; (c)(d) vertical direction; (e)(f) diagonal direction

下载图片查看所有图片

表 1. 密文图像水平、垂直和对角方向上的相关系数比较

Table 1. Comparison of correlation coefficients in horizontal, vertical, and diagonal directions of ciphertext image

Image	Horizontal correlation coefficient of Ref. [8]	Horizontal correlation coefficient of ours	Vertical correlation coefficient of Ref. [8]	Vertical correlation coefficient of ours	Diagonal correlation coefficient of Ref. [8]	Diagonal correlation coefficient of ours
Figure 8(a)	0.0877	0.0078	0.1379	0.0069	0.0349	-0.0046
Figure 8(d)	0.1545	0.0127	0.1002	-0.0039	0.0261	-0.0172
Figure 8(g)	0.1296	-0.0176	0.1249	0.0102	0.0483	0.0261
Figure 8(j)	0.1357	-0.0279	0.1525	0.0200	0.0074	-0.0154

查看所有表

从表1可以看出,在4个测试图像上,经本文方法加密后的图像比采用文献[ 8]中方法加密后的图像在水平、垂直和对角方向上的相邻像素相关系数绝对值更低,绝对值平均分别低了0.110375,0.118625,0.01335。

5.5 加密效果分析

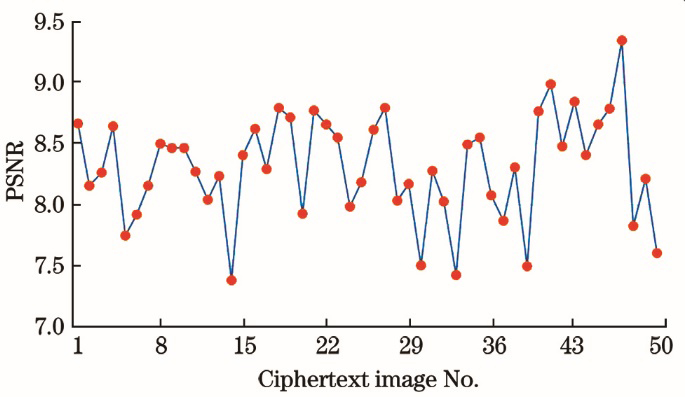
峰值信噪比(PSNR,其值为P_SNR)是一种评价图像质量的指标,其值越高就证明图像间差距越小。设T是图像像素个数,P(i,j)和C(i,j)分别是明文图像和密文图像在(i,j)点上的像素值,I_max是密文图像上最大的像素值,峰值信噪比的计算式^[24]为

\begin{array}{l} E_{MSE} = \frac{\overset{}{\sum_{j}} \overset{}{\sum_{i}} {[P (i, j) - C (i, j)]}^{2}}{T} \times 100 %, (13) \\ P_{SNR} = 10 \lg (\frac{I_{\max}^{2}}{E_{MSE}}) 。 (14) \end{array}

分别计算50张明文图像与相应加密后图像的峰值信噪比,计算结果如图9所示。文献[ 8]和本文方法得到的峰值信噪比分别为14.8843和8.3098。本文方法加密后的图像比经文献[ 8]中方法加密后图像的峰值信噪比低了6.5745,说明经本文方法加密后的图像与原图像差距更大,加密效果更佳。

图 9. 密文图像和明文图像的峰值信噪比

Fig. 9. PSNR of ciphertext image and plaintext image

下载图片查看所有图片

5.6 解密效果分析

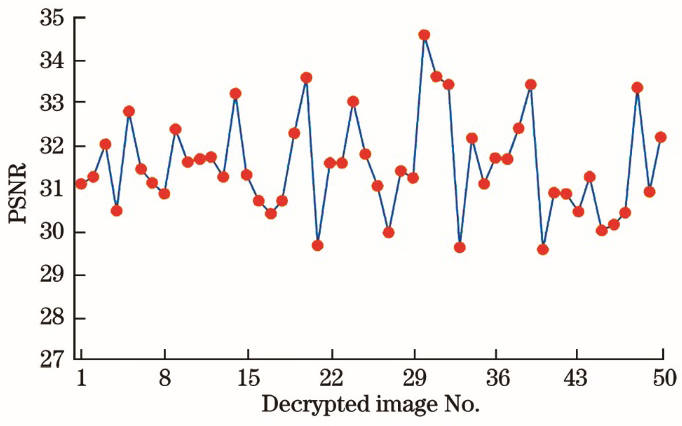
结构相似性(SSIM)也是一个判别图像相似度的指标,图像结构越相似,SSIM的值越高。设μ_x和μ_y分别是图像x和y的均值,σ_x和σ_y分别是图像x和y的方差,σ_xy是图像x和y的协方差,α、β和γ是三个大于0的参数,C₁、C₂和C₃是三个常数,则 SSIM的计算方法为^[25]

V_{SSIM} = {(\frac{2 μ_{x} μ_{y} + C_{1}}{μ_{x}^{2} + μ_{y}^{2} + C_{1}})}^{α} \cdot {(\frac{2 σ_{x} σ_{y} + C_{2}}{σ_{x}^{2} + σ_{y}^{2} + C_{2}})}^{β} \cdot {(\frac{σ_{xy} + C_{3}}{σ_{x} σ_{y} + C_{3}})}^{γ} 。 (15)

分别计算50张测试图像与相应解密后图像与明文图像的峰值信噪比和结构相似性,计算结果如表2、图10和图11所示。本文方法加密后的图像比文献[ 8]方法解密后图像的PSNR值高了1.4075,SSIM值高了0.0428。这说明本文方法解密后的图像与原图像更相似,解密效果更好。

表 2. 文献[ 8]中方法与本文方法得到的峰值信噪比、结构相似性比较

Table 2. Comparison of PSNR and SSIM obtained by method in Ref. [8] and proposed method

Index	Ref. [8]	Proposed method
PSNR	30.1664	31.5739
SSIM	0.9081	0.9509

查看所有表

图 10. 解密图像和明文图像的峰值信噪比

Fig. 10. PSNR of decrypted image and plaintext image

下载图片查看所有图片

图 11. 解密图像和明文图像的结构相似性

Fig. 11. SSIM of decrypted image and plaintext image

下载图片查看所有图片

6 结论

光学图像加密是保护图像隐私的一种重要手段。针对光学图像加密依赖光学仪器精度的问题,使用神经网络模仿双随机相位编码,这摆脱了传统加密方法对光学仪器性能的依赖。采用本文方法对不同的光学图像进行测试,得到良好的加密和解密效果。将本文方法与基于CycleGAN的光学图像加密算法进行对比,可以看出本文方法的实现更简单,加密后图像的PSNR值下降了6.5745,水平、垂直和对角方向上的相邻像素相关系数绝对值平均分别低了0.110375,0.118625,0.01335,解密后图像的PSNR值上升了1.4075,SSIM值高了0.0428。而本文方法在加密速度上还有提升空间,未来需要研究如何设计更快速的加密方法。

参考文献

[1] 郭媛, 敬世伟, 许鑫, 等. 基于矢量分解和相位剪切的非对称光学图像加密[J]. 红外与激光工程, 2020, 49(4): 0426001.

Guo Y, Jing S W, Xu X, et al. Asymmetric optical image encryption based on vector decomposition and phase-truncated[J]. Infrared and Laser Engineering, 2020, 49(4): 0426001.

[2] 薛娟, 刘萍. 基于混沌Gyrator变换与离散小波变换的多图像光学同步加密算法[J]. 电子测量与仪器学报, 2019, 33(11): 136-146.

Xue J, Liu P. Multi-image optical encryption algorithm based on fusion of chaotic Gyrator transform and discrete wavelet transform[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(11): 136-146.

[3] 郭媛, 敬世伟. 基于L-L级联混沌与矢量分解的无损压缩光学图像加密[J]. 光子学报, 2020, 49(7): 0710002.

Guo Y, Jing S W. Lossless compression optical image encryption based on L-L cascade chaos and vector decomposition[J]. Acta Photonica Sinica, 2020, 49(7): 0710002.

[4] 胡耀华, 刘艳, 穆鸽, 等. 基于多模光纤散斑的压缩感知在光学图像加密中的应用[J]. 物理学报, 2020, 69(3): 20191143.

Hu Y H, Liu Y, Mu G, et al. Application of compressive sensing based on multimode fiber specklegram in optical image encryption[J]. Acta Physica Sinica, 2020, 69(3): 20191143.

[5] 王雪光, 李明, 于娜娜, 等. 基于空间角度复用和双随机相位的多图像光学加密方法[J]. 物理学报, 2019, 68(24): 20191362.

Wang X G, Li M, Yu N N, et al. Multiple-image encryption method based on spatial angle multiplexing and double random phase encoding[J]. Acta Physica Sinica, 2019, 68(24): 20191362.

[6] MadonoK, TanakaM, OnishiM, et al. Block-wise scrambled image recognition using adaptation network[EB/OL]. (2020-01-21)[2021-02-15]. https://arxiv.org/abs/2001.07761.

[7] Ding Y, Wu G Z, Chen D J, et al. DeepEDN: a deep-learning-based image encryption and decryption network for Internet of medical things[J]. IEEE Internet of Things Journal, 2021, 8(3): 1504-1518.

[8] 李锦青, 周健, 底晓强. 基于循环生成对抗网络的学习型光学图像加密方案[J]. 吉林大学学报(工学版), 2021, 51(3): 1060-1066.

Li J Q, Zhou J, Di X Q. A learning optical image encryption scheme based on CycleGAN[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(3): 1060-1066.

[9] Hinton GE, Zemel RS. Autoencoders, minimum description length and Helmholtz free energy[C] //Proceedings of the 6th International Conference on Neural Information Processing Systems (NIPS’93). November, 1993, Denver, Colorado, USA. San Francisco: Morgan Kaufmann Publishers Inc., 1993: 3- 10.

[10] Chandar A PS, LaulyS, LarochelleH, et al. An autoencoder approach to learning bilingual word representations[C] //Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 2 (NIPS’14), December 8-13, 2014, Montreal, Quebec, Canada.Cambridge: MIT Press, 2014: 1853- 1861.

[11] Zeng K, Yu J, Wang R X, et al. Coupled deep autoencoder for single image super-resolution[J]. IEEE Transactions on Cybernetics, 2017, 47(1): 27-37.

[12] Xu J, Xiang L, Liu Q S, et al. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images[J]. IEEE Transactions on Medical Imaging, 2016, 35(1): 119-130.

[13] MimuraM, SakaiS, KawaharaT. Exploring deep neural networks and deep autoencoders in reverberant speech recognition[C] //2014 4th Joint Workshop on Hands-free Speech Communication and Microphone Arrays (HSCMA), May 12-14, 2014, Villers-les-Nancy, France.New York: IEEE Press, 2014: 197- 201.

[14] Gogna A, Majumdar A, Ward R. Semi-supervised stacked label consistent autoencoder for reconstruction and analysis of biomedical signals[J]. IEEE Transactions on Biomedical Engineering, 2017, 64(9): 2196-2205.

[15] Wang Z Y, Wang Z J, Fan L, et al. A hybrid Wi-Fi fingerprint-based localization scheme achieved by combining fisher score and stacked sparse autoencoder algorithms[J]. Mobile Information Systems, 2020, 2020: 1-14.

[16] Hou L, Nguyen V, Kanevsky A B, et al. Sparse autoencoder for unsupervised nucleus detection and representation in histopathology images[J]. Pattern Recognition, 2019, 86: 188-200.

[17] Ma L J, Zhang Y T, Li J Q, et al. Community-aware dynamic network embedding by using deep autoencoder[J]. Information Sciences, 2020, 519: 22-42.

[18] 彭翔, 汤红乔, 田劲东. 双随机相位编码光学加密系统的唯密文攻击[J]. 物理学报, 2007, 56(5): 2629-2636.

Peng X, Tang H Q, Tian J D. Ciphertext-only attack on double random phase encoding optical encryption system[J]. Acta Physica Sinica, 2007, 56(5): 2629-2636.

[19] Zhu JY, ParkT, IsolaP, et al.Unpaired image-to-image translation using cycle-consistent adversarial networks[C] //2017 IEEE International Conference on Computer Vision (ICCV), October 22-29, 2017, Venice, Italy.New York: IEEE Press, 2017: 2242- 2251.

[20] Duan X T, Li B X, Xie Z M, et al. High-capacity information hiding based on residual network[J]. IETE Technical Review, 2021, 38(1): 172-183.

[21] He KM, Zhang XY, Ren SQ, et al.Deep residual learning for image recognition[C] //2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 27-30, 2016, Las Vegas, NV, USA.New York: IEEE Press, 2016: 770- 778.

[22] UlyanovD, VedaldiA, LempitskyV, et al. Instance normalization: the missing ingredient for fast stylization[EB/OL]. (2016-07-27)[2021-02-15]. https://arxiv.org/abs/1607.08022.

[23] Kandar S, Chaudhuri D, Bhattacharjee A, et al. Image encryption using sequence generated by cyclic group[J]. Journal of Information Security and Applications, 2019, 44: 117-129.

[24] Man Z L, Li J Q, Di X Q, et al. An image segmentation encryption algorithm based on hybrid chaotic system[J]. IEEE Access, 2019, 7: 103047-103058.

[25] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612.

鲍震杰, 薛茹. 基于自动编码器的光学图像加密方法[J]. 激光与光电子学进展, 2021, 58(22): 2210011. Zhenjie Bao, Ru Xue. Optical Image Encryption Method Based on Autoencoder[J]. Laser & Optoelectronics Progress, 2021, 58(22): 2210011.

基于自动编码器的光学图像加密方法 下载： 1037次

1 引言

2 自动编码器

3 双随机相位编码

图 1. 双随机相位编码架构

Fig. 1. Architecture of double random phase encoding

4 自动光学图像加密网络

图 2. 自动光学图像加密网络的结构

Fig. 2. Structure of automatic optical image encryption network

4.1 损失函数

4.2 神经网络结构

图 3. 自动光学图像加密网络的神经网络结构

Fig. 3. Neural network structure of automatic optical image encryption network

4.3 模型训练和图像加解密过程

5 实验结果与分析

5.1 实验环境

5.2 模型收敛性

图 4. 编码损失函数随迭代次数的变化

Fig. 4. Change of encoding loss function with iterations

图 5. 解码损失函数随迭代次数的变化

Fig. 5. Change of decoding loss function with iterations

5.3 实验结果

图 6. 自动光学图像加密网络的加密解密效果。(a)原始图像;(b)加密图像;(c)解密图像

Fig. 6. Encryption and decryption effects of automatic optical image encryption network。(a) Original images;(b) encryption images; (c) decryption images

5.4 抗统计攻击分析

图 7. 自动光学图像加密网络的明文图像、加密图像与解密图像的直方图。(a)明文图像;(b)加密图像;(c)解密图像

Fig. 7. Histograms of plaintext images, encrypted images, and decrypted images in automatic optical image encryption network. (a) Plaintext images; (b) encrypted images; (c) decrypted images

图 8. 明文图像与密文图像的水平、垂直和对角方向上的相邻像素散点图。(a)(b)水平方向;(c)(d)垂直方向;(e)(f)对角方向

Fig. 8. Scatter plots of adjacent pixels in horizontal, vertical, and diagonal directions of plaintext image and ciphertext image. (a)(b) Horizontal direction; (c)(d) vertical direction; (e)(f) diagonal direction

表 1. 密文图像水平、垂直和对角方向上的相关系数比较

Table 1. Comparison of correlation coefficients in horizontal, vertical, and diagonal directions of ciphertext image

5.5 加密效果分析

图 9. 密文图像和明文图像的峰值信噪比

Fig. 9. PSNR of ciphertext image and plaintext image

5.6 解密效果分析

表 2. 文献[ 8]中方法与本文方法得到的峰值信噪比、结构相似性比较

Table 2. Comparison of PSNR and SSIM obtained by method in Ref. [8] and proposed method

图 10. 解密图像和明文图像的峰值信噪比

Fig. 10. PSNR of decrypted image and plaintext image

图 11. 解密图像和明文图像的结构相似性

Fig. 11. SSIM of decrypted image and plaintext image

6 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于自动编码器的光学图像加密方法下载： 1037次