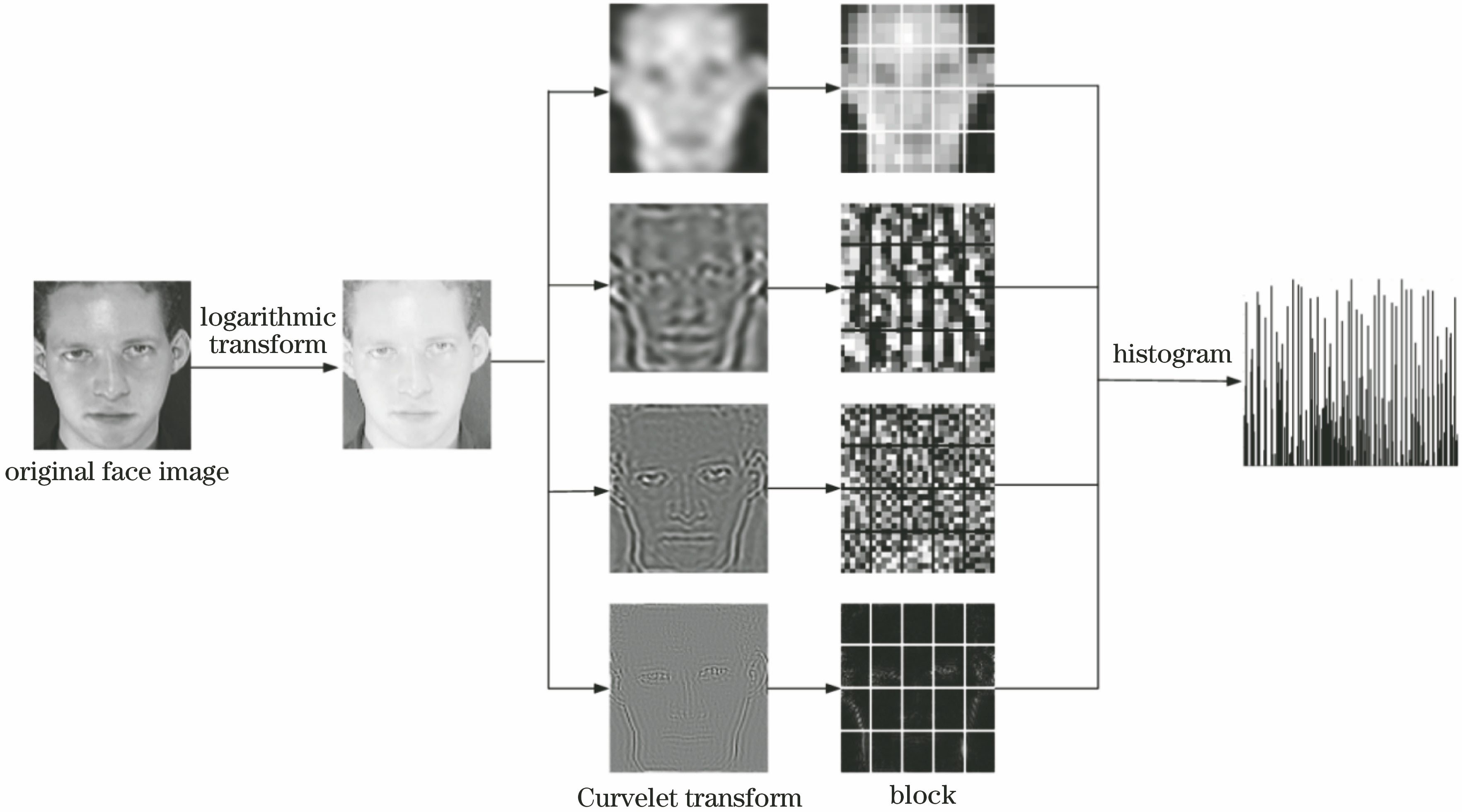
基于自适应加权Curvelet梯度方向直方图的人脸识别算法

杨恢先; 李笑笑; 甘伟发

doi:doi:10.3788/LOP57.101011

激光与光电子学进展, 2020, 57 (10): 101011, 网络出版: 2020-05-08

基于自适应加权Curvelet梯度方向直方图的人脸识别算法下载： 1171次

A Face Recognition Algorithm Based on Adaptive Weighted Curvelet Gradient Direction Histogram

论文大纲

杨恢先李笑笑 ^*甘伟发

作者单位

湘潭大学物理与光电工程学院, 湖南湘潭 411105

Physics and Optoelectronic Engineering College, Xiangtan University, Xiangtan, Hunan 411105, China

图像处理人脸识别 Curvelet变换梯度方向直方图 image processing face recognition Curvelet transform gradient direction histogram

AI词云图 AI语音精读 AI语音超短摘要

注：本部分内容由 AI 自动生成，仅供您参考。对于您使用本站 AI 自动生成内容所产生的一切后果，本网站及平台运营方概不承担任何商业和法律责任，请您知悉。

摘要

提出一种基于自适应加权Curvelet梯度方向直方图(AWCHOG)的人脸识别算法。首先,人脸图像通过基于Wrapping的离散Curvelet变换得到多尺度多方向的Curvelet变换系数;然后按照编码方式将同一尺度下不同方向的特征进行编码融合,获得融合后的幅值域图谱,并通过HOG算子结合分块的方法获得Curvelet变换后融合图像的直方图特征,分别根据每个尺度对人脸识别率的贡献进行计算,得出各尺度的权重;最后融合权重系数以及各尺度的HOG特征,利用最近邻分类器进行分类。通过在ORL、AR和CAS-PEAL三个人脸库的实验可以看出,所提算法在人脸图像部分遮挡、姿态、表情、光照变化以及噪声等因素干扰下具有较好的识别效果。

Abstract

Herein, a face recognition algorithm based on an adaptive weighted Curvelet gradient direction histogram is proposed. First, the Curvelet transform based Wrapping is used to extract facial features with multi-orientations, and the coding method is exploited to fuse the original Curvelet features that have the same scale. Second, the fused image is divided into numerous equal-sized non-overlapping rectangular blocks. The face image is then described using the histogram sequence extracted from all the blocks using the HOG operator, and the adaptive weighting of histograms with each scale is separately performed. Finally, the extracted features are fed into the nearest neighbor-based classifier. Results of the simulation experiments conducted using the ORL, YALE, and CAS-PEAL face databases show that the proposed algorithm has a high face recognition rate and good robustness under the influence of interference factors such as face occlusion, gesture transformation, expression transformation, and illumination transformation.

1 引言

随着计算机的出现和人工智能的兴起,具有智能理解和信息感知的模式识别受到越来越多的关注。生物特征识别作为模式识别中的重要研究领域,已经获得了极大的发展。人脸识别系统的图像采集过程非常开放,具有非接触性和非侵害性的特点,成为一种被人们广泛接受的生物特征识别技术。人脸是人的内在属性,具有很强的自身稳定性和个体差异性。因此,人脸识别是生物特征识别中最主要的方法之一,也是模式识别的前沿研究领域,在信息和公共安全等相关领域具有良好的应用前景。梯度方向直方图(HOG)是一种局部特征提取算子,能够获取图像的更多梯度方向信息,并且对于光照、尺度、方向等有很好的鲁棒性^[1],被广泛应用在人脸识别算法^[2]、行人重识别算法^[3]中,并取得了较好的识别效果。人脸识别实质上是特征提取和分类的过程,近几年来,各种多分辨率分析的方法已经被越来越多地用于人脸特征提取,例如小波变换、Gabor变换^[4]、Curvelet变换等。被称为“数字显微镜”的小波变换具有多分辨率的特点,在很多领域得到了广泛应用,但是小波变换的基是各向同性的,不具有各向异性的特点,仅能反映一维信号中奇异点的性质,无法表达二维图像的“沿”边缘特征,无法最优表示二维图像的奇异曲线^[5]。与小波变换相比,Curvelet变换在处理曲线上具有显著的优势,它不仅具有较小的噪声含量,拥有小波变换的多分辨率特性和时频局域特性,还具有非常强的方向性和各向异性,能够提取更多曲线的细节特征,更精确地表现人脸的重要信息。近些年来研究人员提出了许多基于Curvelet变换的改进算法。李艳萍等^[6]提出基于曲波变换和余弦测度人脸识别的算法,有效降低了特征维度,但没有充分考虑系数间的相关性。周立俭等^[7]提出基于Curvelet 变换和局部二值模式(LBP)的可变光照的识别方法,该方法对于光照变化有较好的鲁棒性,但是舍弃了高频信息。赵庆敏等^[8]提出了Curvelet变换结合双向二维主成分分析[(2D)²2PCA]的人脸识别算法,虽然减少了运算时间,但舍弃了许多细节特征,导致信息提取不充分。

为了能够提取更多人脸图像的识别特征,改善人脸识别系统的识别效果,本文提出一种自适应加权Curvelet梯度方向直方图(AWCHOG)的人脸识别算法。在对人脸图像进行多尺度多方向的Curvelet变换分解后,考虑到不同尺度层所含的信息量不同,首先对第一、第四尺度系数取幅值信息,对第二、第三尺度系数进行编码融合,然后分别对融合后的四个尺度特征进行最佳分块数的HOG特征提取并进行自适应加权,最后使用最近邻分类器进行分类。

2 基本原理

2.1 Curvelet变换概述

Curvelet变换最先由Candes等^[9]提出,它能够在很大程度上弥补图像边缘信息处理时小波变换所存在的缺乏奇异性的弱点,能够准确地提取多个尺度、多个方向上的曲线信息,拥有良好的去噪性能。Curvelet变换有两代演变,第一代Curvelet变换是以脊波变换理论为基础,其过程主要是先对图像进行子带分解,然后将不同尺度的子带图像平滑分块并规范化,最后实现脊波变换^[10]。第一代Curvelet变换虽然能够很好地处理图像边缘信息缺失问题,但也会提高运算的复杂度,并且导致数据冗余,不利于调试工作的开展。因此,2005年Candes 等^[11]提出了第二代Curvelet变换。第二代Curvelet变换的方法结构完全不同于第一代,第二代Curvelet变换与脊波变换并不存在理论上的直接联系,参数少且运算简单,与第一代相比较,第二代Curvelet变换的细节处理效果更好,更适用于人脸识别算法。本文采用第二代Curvelet变换,使用曲波变换的离散形式对人脸图像进行特征提取,并选取运算速度比较快、算法效率较高的基于Wrapping 的快速离散Curvelet变换算法^[12]。以笛卡儿坐标系下的f(t₁,t₂)(0≤t₁,t₂<n)为输入,Curvelet变换的离散形式为

\begin{matrix} c^{D} (j, l, k) = \sum_{0 \leq t_{1}, t_{2} < n} f (t_{1}, t_{2}) {φ^{D}}_{j, l, k} (t_{1}, t_{2}), (1) \end{matrix}

式中: $\begin{matrix} φ_{j, l, k}^{D} \end{matrix}$ 表示离散Curvelet波形;上标D表示离散形式。定义笛卡儿坐标系下的局部窗为

\begin{matrix} \begin{matrix} {\tilde{U}}_{j} (ω) = {\tilde{W}}_{j} (ω) V_{j} (ω), (2) \\ {\tilde{W}}_{j} = \sqrt[]{Φ_{j + 1}^{2} (ω) - Φ_{j}^{2} (ω)}, j \geq 0, (3) \\ V_{j} (ω) = V [2^{floor (j / 2)} \times ω_{2} / ω_{1}], (4) \end{matrix} \end{matrix}

式中: $\begin{matrix} {\tilde{W}}_{j} \end{matrix}$ (ω)为带通“径向窗”函数;V为“角度窗”函数;Φ为一维低通窗口内积,

\begin{matrix} Φ_{j} (ω_{1}, ω_{2}) = φ (2^{- j} ω_{1}) φ (2^{- j} ω_{2}), 0 < φ < 1 。 (5) \end{matrix}

引入相同间隔斜率 $\begin{matrix} \tan θ_{l} = l \times 2^{- floor (j / 2)}, l = - 2^{floor (j / 2)}, \dots, 2^{floor (j / 2)} - 1, \end{matrix}$ 则有

\begin{matrix} {\tilde{U}}_{j, l} (ω) = {\tilde{W}}_{j} (ω) V_{j} (S_{θl} ω), (6) \end{matrix}

式中:S_θl为剪切矩阵, $\begin{matrix} S_{θl =} [\begin{matrix} 1 & 0 \\ - tanθ & 1 \end{matrix}]; θ_{l} 并非等间距的, \end{matrix}$ 但斜率是等间距的。

基于 Wrapping离散的Curvelet 变换算法的步骤如下:

1) 对给定的二维函数f(t₁,t₂)(0≤t₁,t₂<n)进行傅里叶变换,可以得到二维频域表示 $\begin{matrix} \hat{f} \end{matrix}$ (n₁,n₂),-n/2≤n₁,n₂<n/2;

2) 对于每一个分解的尺度j和方向l,将 $\begin{matrix} \hat{f} \end{matrix}$ (n₁,n₂)重新采样后的 $\begin{matrix} \hat{f} \end{matrix}$ (n₁,n₂-n₁tanθ_l)与窗函数 $\begin{matrix} {\tilde{U}}_{j} \end{matrix}$ (n₁,n₂)相乘可以得到

\begin{matrix} \hat{f} (n_{1}, n_{2}) = \hat{f} (n_{1}, n_{2} - n_{1} \tan θ_{l}) {\tilde{U}}_{j} (n_{1}, n_{2}); (7) \end{matrix}

3) 围绕原点Wrapping离散,上述乘积可表示为 $\begin{matrix} {\hat{f}}_{j, l} (n_{1}, n_{2}) = W [{\tilde{U}}_{j, l}, \hat{f} (n_{1}, n_{2})], 其中 0 \leq n_{1} < L_{1, j}, 0 \leq n_{2} < L_{2, j}, L_{1, j} 和 L_{2, j} 分别为关于 2^{j} 和 2^{\frac{j}{2}} 的参量 \end{matrix}$ ;

4) 对每个 $\begin{matrix} {\hat{f}}_{j, l} \end{matrix}$ 进行二维傅里叶逆变换,就可以得到Curvelet变换特征系数c^D(j,l,k)。

2.2 HOG

将人脸图像分割成一个个小的连通区域——细胞单元,然后以细胞单元为单位,计算和统计各细胞单元中每个像素梯度或者边缘方向的直方图,并将所有细胞单元的直方图串接起来组成图像的特征描述子。HOG特征提取过程为^[13]

1) 采用中心对称的梯度算子来计算人脸图像上每个像素点的梯度方向和幅值信息,其计算过程分别为

\begin{matrix} \begin{matrix} θ (x, y) = \arctan [\frac{I (x, y + 1) - I (x, y - 1)}{I (x + 1, y) - I (x - 1, y)}], (8) \\ m (x, y) = {\{[I (x, y + 1) - I {(x, y - 1)]}^{2} + [I (x + 1, y) - I {(x - 1, y)]}^{2}\}}^{\frac{1}{2}}, (9) \end{matrix} \end{matrix}

式中:I(x,y)为人脸图像上点(x,y)的像素值;θ(x,y)为该点的梯度方向;m(x,y)为该点的梯度幅值。

2) 在每个像素胞元内统计梯度直方图,将0到180°的方向空间等分为n个区间(称之为梯度方向数),对应区间的梯度幅值按权值1相加到匹配的梯度方向上。

3) 将每个像素胞元内的直方图采用L₂标准化,并将所有胞元的直方图串接起来形成整个人脸的HOG特征。标准化公式为

\begin{matrix} v \to v / \sqrt[]{‖v ‖_{2}^{2} + ε^{2}}, (10) \end{matrix}

式中:v为标准化之前的直方图向量;ε是一个极小的常量,以防止计算得到无穷大值。

2.3 AWCHOG

Curvelet变换能够从人脸图像中提取出更多细节信息,HOG特征具有对光照、旋转等因素的强鲁棒性且易于计算等特点,鉴于Curvelet变换特征维数过高,受到文献[ 14]和文献[ 15]的启发,本文提出一种改进算法——AWCHOG人脸识别算法。AWCHOG算法由两个部分组成,分别是Curvelet变换的系数编码融合以及自适应加权的HOG算子。

2.3.1 Curvelet多方向特征融合

通过对人脸图像进行Curvelet变换,可以得到不同尺度、不同方向的人脸细节特征,但较多的细节特征会导致特征冗余并在接下来的人脸识别中增加算法的复杂度。而且经过Curvelet变换后得到的各尺度、各方向的Curvelet系数虽能够准确描述人脸特征,但是若直接将Curvelet系数输入到人脸识别的分类器中,由于Curvelet系数间有一定的信息冗余,人脸识别的识别率低,识别效果不佳,为此本文提出一种基于实部特征的编码方法。

Curvelet变换涉及2个重要参数,即Curvelet变换的分解尺度与方向数。如果分解的尺度过小,则数据无法获得很好的压缩并且无法获取大量细节信息;如果分解尺度过大,则会造成数据维度过多,还会丢失图像的部分特征。分解的尺度可表示为

\begin{matrix} s = c e iling \{lo g_{2} [\min (m, n)] - 3\}, (11) \end{matrix}

式中:m、n分别表示图像的长和宽。对于尺寸大小为128 pixel×128 pixel的人脸图像,分解的尺度为4。对于方向的选择,各尺度层方向数必须是4的倍数,实验中第1层和第4层无须设定方向,第2层方向数设定为8,第3层设定为16。

对人脸图像进行Curvelet分解后,各层系数矩阵形式如表1所示。

表 1. 112 pixel×92 pixel人脸图像经过Curvelet变换后的系数形式

Table 1. Form of Curvelet coefficients after Curvelet transform for 112 pixel×92 pixel face image

Coefficient level	Coefficient matrix form	Dimension
Coarse	19×15 matrix	285
Detail 1	1×8 cell consisting of the matrix of size 17×31 or 37×15	4328
Detail 2	1×16 cell consisting of the matrix of size 32×31 or 28×30 or 38×26 or 38×23	14776
Fine	112×92 matrix	10304

查看所有表

1) 分别对第一、第四尺度取幅值信息,并进行双边滤波处理,去除噪声影响。

2) 对第二、第三尺度下不同方向的图像像素点进行编码融合。第二尺度选择8个方向,第三尺度选择与第二尺度不同的8个方向。

\begin{matrix} P_{j, l} (z) = \{\begin{matrix} 1, Re [c_{j, l} (z)] > 0 \\ 0, Re [c_{j, l} (z)] \leq 0 \end{matrix}, (12) \end{matrix}

式中:c_j_,_l(z)为图像中每个像素点z(x,y)对应的多尺度、多方向的Curvelet特征,j∈(1,…,4),表示分解的尺度,l∈(0,1,…,7),表示分解的方向;Re[c_j_,_l(z)]对应z(x,y)点的像素值实部。各尺度下的多方向融合的二进制编码可表示为

\begin{matrix} T_{j} (z) = \overset{7}{\sum_{l = 0}} P_{j, l} \times 2^{l}, (13) \end{matrix}

式中:T_j(z)∈[0,255]。由此得出十进制的编码值,最终得到的4幅各尺度融合图像如图1所示。

图 1. 四个尺度融合图像。(a)尺度1;(b)尺度2;(c)尺度3;(d)尺度4

Fig. 1. Fusion images at four scales. (a) Scale 1; (b) scale 2; (c) scale 3; (d) scale 4

下载图片查看所有图片

2.3.2 自适应HOG特征加权

由于不同人脸区域包含不同的人脸信息,对人脸识别有不同的贡献,因此有必要对具有更高贡献的人脸区域赋予更高的权重,以突出这些人脸区域的特征。人脸图像经过Curvelet变换后被分为三个层次(coarse层、中间detail层和fine层),由于每个层次所含的信息不同,对于识别率的贡献也不尽相同,其中coarse层由低频系数矩阵组成,反映了图像的概貌特征,所含信息最多。detail层由中高频系数矩阵组成,包含了图像的主要边缘特征。fine层由高频系数矩阵组成,包含了图像的高频轮廓信息。最理想的加权方法是:当某子块拥有的识别信息越多时,其分配的权重也就越大。因此,本文用HOG算子分别依据每个层次最佳分块数提取特征,最后基于各层次最优识别率来分别计算融合后的4个尺度的权值w_l。权值w_l的计算步骤如下:

步骤1 首先对人脸图像进行对数变换;

步骤2 对人脸库的图像按照2.3.1节方法融合成4个尺度的图像;

步骤3 用HOG算子分别对融合后的4个尺度图像进行特征提取并求出识别率,得出每个尺度的最佳分块数n×m,以及识别率δ_l;

步骤4 将各尺度得到的识别率按照w_l= $\begin{matrix} \frac{1}{1 - δ_{l}} \end{matrix}$ (l=1,2,3,4)进行计算,分别得到各尺度融合图像的权值w_l,权值会随着识别率δ_l的增大而增大。

3 AWCHOG算法的人脸识别

3.1 AWCHOG特征提取

基于AWCHOG的人脸识别算法特征提取具体步骤为

1)首先对人脸图像进行对数变换,去除一定的光照干扰,然后进行Curvelet变换,分解成多尺度多方向特征;

2)分别按照 2.3.1 节和 2.3.2节中介绍的算法对Curvelet系数进行编码融合,并对融合后特征进行自适应HOG特征提取,然后对特征进行自适应加权形成复合特征。

AWCHOG算法流程如图2所示。

3.2 人脸匹配

在进行特征识别的过程中,将测试样本和训练样本的AWCHOG直方图序列特征之间相交的距离作为其相似度测量的依据。2个直方图序列的相似度可表示为

\begin{matrix} S_{im} (H_{1}, H_{2}) = \overset{N}{\sum_{i = 1}} \min [h_{1} (i), h_{2} (i)], (14) \end{matrix}

式中:H₁和H₂为两个对比直方图序列特征;N是直方图箱格(bin)的数量;h₁(i)和h₂(i)分别为两个直方图中第i个箱格(bin)出现的频率。

4 实验结果与分析

实验环境为MATLAB R 2016a,64位Windows 10系统,Intel(R)Core(TM)i5-7300CPU,3.6 GHz,12 GB 内存。

ORL人脸库包含40个人,每人10幅图像,在表情、性别和姿态等方面均有变化,本次实验中,训练集由随机抽取的每人2~6幅人脸图像组成,剩余的人脸图像则作为测试集。本次实验将人脸图像裁剪成112 pixel×92 pixel,重复进行10次实验后,将实验结果的均值作为最终的人脸识别率。ORL人脸库中某个样本的部分人脸图像如图3所示。

图 2. AWCHOG算法流程图

Fig. 2. Flow of AWCHOG algorithm

下载图片查看所有图片

图 3. ORL人脸库。(a)图像1;(b)图像2;(c)图像3;(d)图像4;(e)图像5;(f)图像6

Fig. 3. ORL face dataset. (a) Image 1; (b) image 2; (c) image 3; (d) image 4; (e) image 5; (f) image 6

下载图片查看所有图片

AR人脸库包含了4000多幅人脸图像,分别来自56个女性和70个男性。这些图像分别在光照、表情和遮挡上有变化。选取该人脸库中的50名女性和50名男性,取每人的13幅图像组成4个测试集(光照集、表情集、遮挡集A和遮挡集B),本次实验人脸图像裁剪成165 pixel×120 pixel,选取每个人的第一幅正脸图像作为训练样本,人脸库中某个样本的人脸图像如图4所示。

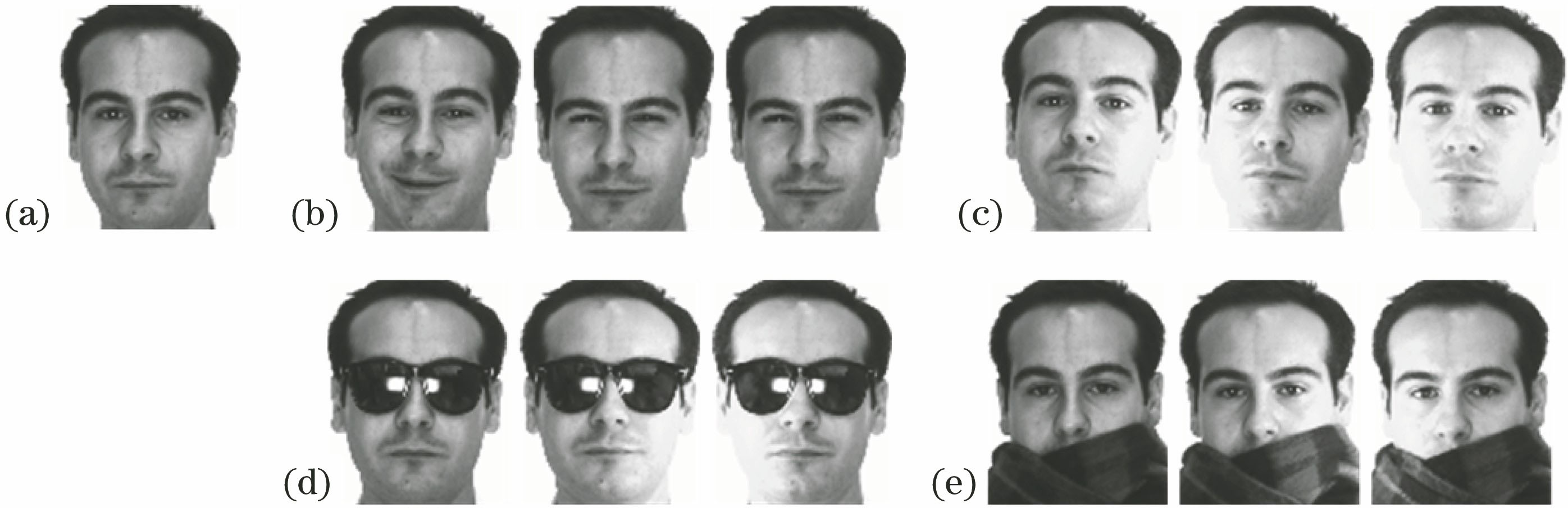
图 4. AR人脸库。 (a)训练样本;(b)表情集;(c)光照集;(d)遮挡集A;(e)遮挡集B

Fig. 4. AR face dataset. (a) Training sample; (b) facial express subset; (c) illumination subset; (d) partial occlusion subset A; (e) partial occlusion subset B

下载图片查看所有图片

CAS-PEAL人脸库包含了1040人共计99450幅人脸图像,其中变化环境包括背景、光照、饰物、表情和姿态等。本次实验中人脸图像被裁剪成100 pixel×100 pixel,随机选取200人用于实验。将200个人的部分图像组成3个测试集(饰物集、背景集和表情集),将第一幅正面人脸图像作为训练样本,其余作为测试样本,其中某个人的人脸图像如图5所示。

图 5. CAS-PEAL人脸库。 (a)训练样本; (b)表情集; (c)背景集; (d)饰物集

Fig. 5. CAS-PEAL face dataset. (a) Training sample; (b) Express subset; (c) Background subset; (d) Accessory subset

下载图片查看所有图片

4.1 参数对实验效果的影响

为了探究Curvelet分解的不同尺度数目对于实验效果的影响,分别在ORL人脸库、AR表情库和CAS-PEAL表情库上研究识别的分类情况,实验结果见表2。

表 2. Curvelet变换不同尺度下的识别率

Table 2. Recognition rate of Curvelet transform at different scales

Scale	Recognition rate /%
Scale	ORL	AR	CAS-PEAL
1	90.00	91.00	98.14
2	92.50	92.33	98.54
3	93.00	94.67	98.89
4	95.50	95.67	99.20
5	89.50	90.67	95.94

查看所有表

从表2可以看出,过多的尺度变换会丢失许多重要的特征信息,过少的尺度变换则会导致特征冗余且降低识别率。因此本文算法中将Curvelet分解为4个尺度的效果最佳。

在对梯度特征的分布进行统计时,选择HOG的分块数和梯度方向数目对提高识别率十分重要,如果分块数过少,难以提取出图像的形状分布特征,而分块数过多会使得特征冗余,并对表情等变化十分敏感,导致识别效果不佳。梯度方向数目的选择也很重要,过少则不能充分体现人脸图像的轮廓信息,丢失很多局部的纹理特征,过多则会降低算法表情、姿态等变化上的识别率,同时也会增加特征的维数和算法的时间度。以ORL人脸库样本数为5时的数据为例,分析不同的梯度方向数目以及分块数对识别率的影响,结果分别如图6和图7所示。

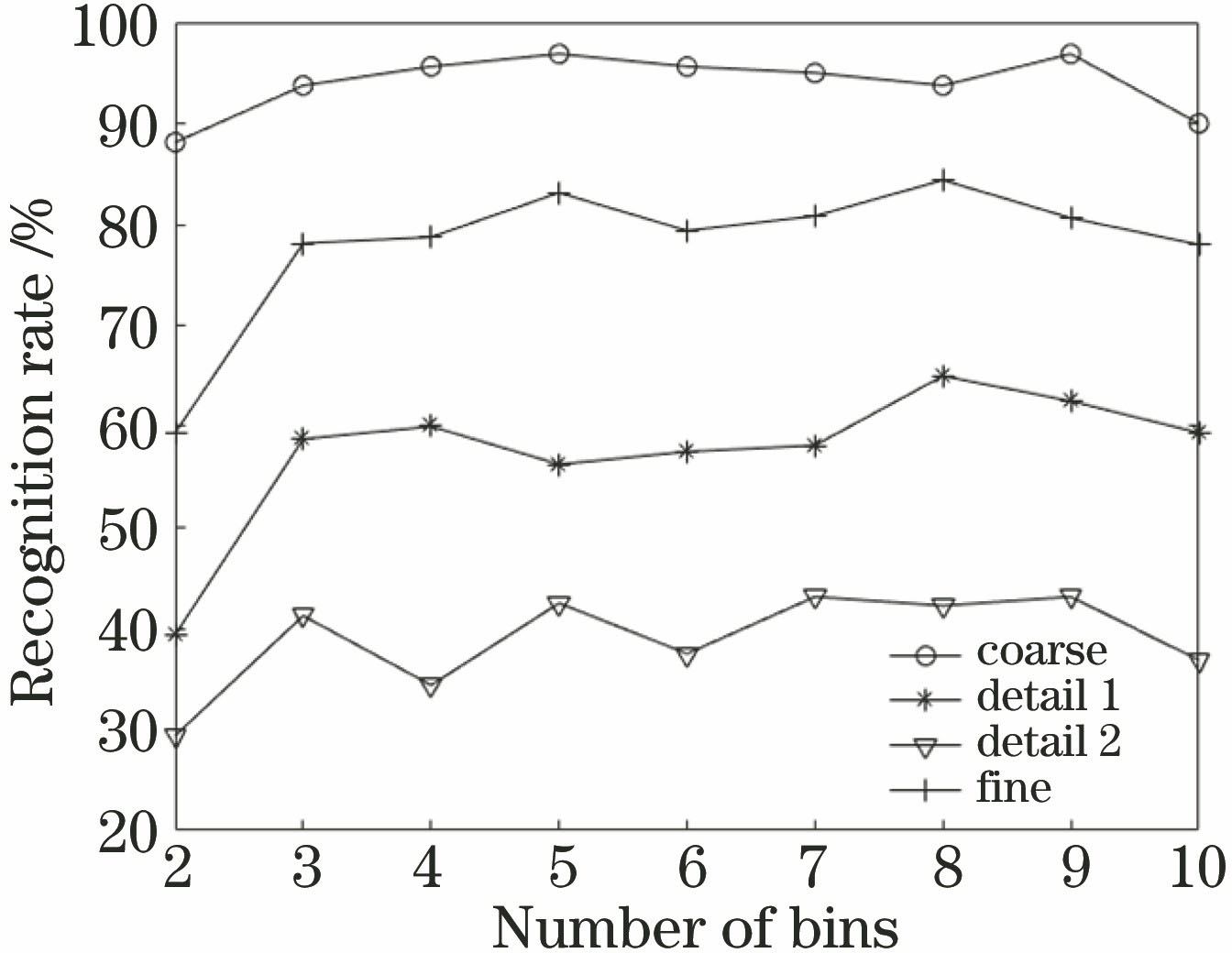
图 6. ORL人脸库在不同梯度方向数下的识别率

Fig. 6. Recognition rate of ORL face dataset at different gradient directions

下载图片查看所有图片

由图7可知,当取不同的分块数时,对人脸的识别率也不同。ORL人脸库包含较多的细节及姿态变化,因此过多的分块会导致识别率下降,增加分块会提升特征维数,从而导致识别时间增加。综合考虑后,在ORL人脸库中,coarse层的最佳分块数为8×5,detail 1层的最佳分块数为10×10,detail 2层的最佳分块数为10×11,fine层的最佳分块数为8×8,明显看出coarse层分块数较于其他层少且识别率要高,主要是因为coarse层为人脸图像的概貌,包含了人脸图像的主要特征信息,含有较多姿态变化,而其他层包含许多细节或轮廓信息。

通过权衡识别时间以及识别率等因素,在AR人脸库的4个子集中,coarse层的最佳分块数为8×8,detail 1层的最佳分块数为10×11,detail 2层的最佳分块数为12×9,fine层的最佳分块数为8×9。在CAS-PEAL库的背景集、饰物集和表情集上,coarse层的最佳分块数为10×10,detail 1层的最佳分块数为12×12,detail 2层的最佳分块数为11×9,fine层为的最佳分块数10×12。

从图6可看出,识别率随着梯度方向数目的增加而变化。增加梯度方向数可以获得更多的识别信息,但同时也会导致特征的维数过多,从而占据更多的内存,使得计算时间增多,并且对表情、姿态等变化越来越敏感。综合考虑到识别率和特征维数等因素,在ORL人脸库的coarse层采用的最佳梯度方向数为9,detail 1层为8,detail 2层为7,fine层为8。在AR人脸库的4个子集上,coarse层采用最佳梯度方向数为7,detail 1层为6,detail 2层为7,fine层为6。在CAS-PEAL库的背景集、饰物集和表情集上,coarse层采用的最佳梯度方向数为8,detail 1层为9,detail 2层为9,fine层为8。

4.2 与其他算法识别率对比

为了验证AWCHOG算法的有效性,分别在ORL人脸库、AR人脸库和CAS-PEAL人脸库进行实验,并将其分别与Wavelet、HOG^[16]、Curvelet+PCA+SRC^[17]、Gabor+HOG以及NSCT+LBP^[18]算法进行比较,为了更好地探讨Curvelet变换的性能,将经典的多尺度几何分析方法NSCT变换用于本文算法(AWNHOG)进行实验对比,6种对比算法均采用最近邻分类器进行分类,对本文算法分别采用最近邻分类器和协作表示分类(CRC)进行分类比较。实验结果如表3~5所示。

图 7. ORL人脸库不同尺度在不同分块方式下的识别率。(a) Coarse层;(b) detail 1层;(c) detail 2层;(d) fine层

Fig. 7. Recognition rate of ORL face dataset in different block modes. (a) Coarse floor; (b) detail 1 floor; (c) detail 2 floor; (d) fine floor

下载图片查看所有图片

表 3. ORL人脸库上的识别率

Table 3. Recognition rate on ORL database

Algorithm	Recognition rate /%
Algorithm	Image 2	Image 3	Image 4	Image 5	Image 6
Wavelet	83.13	88.21	87.92	93.74	96.50
HOG	85.00	89.29	92.50	97.00	96.88
Curvelet+PCA+SRC	88.21	93.33	94.00	95.00	95.83
Gabor+HOG	90.41	94.61	97.21	98.20	98.69
NSCT+LBP	89.14	94.79	96.20	98.11	98.69
AWNHOG	82.25	87.21	91.25	95.00	96.88
AWCHOG+CRC	90.12	86.79	92.50	96.50	97.33
AWCHOG+KNN	90.71	95.50	96.88	98.75	99.27

查看所有表

从表3~5的实验数据对比可以看出,AWCHOG算法的识别率明显高于其他对比算法,尤其在表情和姿态变化方面,AWCHOG算法优势明显。Wavelet算法虽然具有多分辨率的特点,但由于小波变换无法准确表示人脸图像奇异曲线的弱点,无法对含有较多轮廓细节信息和五官曲线信息实现最优的稀疏表示,因此识别率比较低。从表3~5可以看出,Curvelet变换的识别率明显优于小波变换。HOG算子能够提取图像的边缘和形状特征,并且对光照和噪声变化具有一定的鲁棒性,但是从表4和表5可以看出:HOG对于饰物以及遮挡的识别效果不佳,主要是因为在眼部或者嘴部被遮挡的情况下,能提取的边缘轮廓信息减少;Curvelet+PCA+SRC算法使得人脸图像经过 Curvelet变换后获得更多的曲线特征并且拥有最优的稀疏表示,分类效果显著,但受光照影响较大;Gabor+HOG和NSCT+LBP算法可以提取到更多局部信息,在表情、光照及姿态变化方面都获得了良好的识别率。由表3~5可知,本文算法应用最近邻分类器的效果总体上优于协作分类方法。虽然AWNHOG算法在遮挡方面识别率较高,但从整体上来看AWCHOG算法的识别效果更佳。AWCHOG算法通过对人脸图像进行Curvelet变换分解到不同尺度和方向上,系数编码融合后进行自适应HOG特征提取,可以更好地提取各方向的纹理和轮廓信息,同时避免了特征冗余。对表情、光照、遮挡和姿势变化等均具有较强的鲁棒性。

表 4. CAS-PEAL人脸库上的识别率

Table 4. Recognition rate on CAS-PEAL database

Algorithm	Recognition rate /%
Algorithm	Expression subset	Accessory subset	Background subset
Wavelet	96.45	78.61	78.89
HOG	99.20	69.00	93.00
Curvelet+PCA+SRC	97.34	78.89	80.83
Gabor+HOG	99.73	87.22	95.56
NSCT+LBP	99.38	74.25	92.75
AWNHOG	99.63	80.50	99.00
AWCHOG+CRC	99.33	98.67	95.00
AWCHOG+KNN	99.75	97.50	98.50

查看所有表

表 5. AR人脸库上的识别率

Table 5. Recognition rate on AR database

Algorithm	Recognition rate /%
Algorithm	Facial expresssubset	Illuminationsubset	Partial occlusionsubset A	Partial occlusionsubset B
Wavelet	92.67	80.50	79.50	62.00
HOG	91.33	90.33	69.00	49.00
Curvelet+PCA+SRC	94.67	85.50	91.33	73.67
Gabor+HOG	96.33	97.50	81.00	76.50
NSCT+LBP	96.67	98.33	96.67	76.00
AWNHOG	98.33	99.67	96.67	82.67
AWCHOG+CRC	95.33	96.67	93.67	80.33
AWCHOG+KNN	99.50	98.89	96.00	90.00

查看所有表

4.3 加噪实验

为了验证算法的抗噪能力,在AR人脸库光照子集引入均值为0、归一化方差分别设为0.0001、0.0002、0.0003、0.0004的高斯白噪声。选取不加入高斯噪声的AR人脸库光照子集中的标准正面人脸作为训练样本,并将加入高斯白噪声的其余人脸图像作为测试样本,在重复50次实验后,比较实验结果的均值。为了验证各算法对噪声的抵抗能力,采用φ对识别率的变化进行描述:

\begin{matrix} φ = \frac{a - b}{a} \times 100 %, (15) \end{matrix}

式中:a表示在加入高斯白噪声之前算法的识别率;b表示在加入高斯白噪声后算法的识别率;φ为识别率下降的快慢程度,其值的大小与抗噪性能成反比。表6表示加入的高斯白噪声对各算法识别率的影响程度以及抗噪性能的优劣。

从表6可以看出,加入高斯白噪声后,各算法的识别率逐渐开始下降。其中Wavelet算法下降最快,易受光照及噪声影响,因此抗噪能力最差。HOG算法在梯度域产生,抗噪能力略差。由于LBP算法对噪声比较敏感,所以NSCT+LBP算法抗噪声能力较弱。Curvelet+PCA+SRC算法、Gabor+HOG算法识别率下降较慢,有一定的抗噪能力,NSCT变换对于噪声抵抗能力较好。Curvelet变换对噪声不敏感,能够对噪声有一定平滑效果,实验结果表明AWCHOG算法的识别率下降最慢,识别率也最高,对噪声有比较好的鲁棒性。

表 6. 加入高斯噪声后,AR光照库上不同算法的实验结果

Table 6. Results of different algorithms on AR illumination subset after adding Gaussian noise

Method	Normalized variance of Gaussion white noise						φ
Method	0		0.0001		0.0002	0.0003	0.0004
Wavelet	80.50	39.00		21.50	16.67	14.67	81.78
HOG	90.33	68.33		58.67	53.67	52.33	42.06
Curvelet+PCA+SRC	85.50	71.67		68.33	67.67	65.67	23.19
Gabor+HOG	97.50	86.00		84.67	81.00	79.33	18.63
NSCT+LBP	98.33	91.50		85.50	74.00	70.50	28.30
AWNHOG	99.67	93.67		90.33	83.67	79.67	20.06
AWCHOG+KNN	98.89	98.00		96.67	91.67	90.67	8.31

查看所有表

4.4 算法复杂度分析

为了比较各算法的特征维数及识别时间,以ORL人脸库为例,在实验中随机选取一幅人脸图像作为训练样本,其余人脸图像作为测试样本,计算每种算法识别一幅人脸图像所需要的平均时间t,即

\begin{matrix} t = T_{1} + T_{2}, (16) \end{matrix}

式中:T₁为提取一幅人脸图像的特征所需要的平均时间;T₂为完成一幅测试图像的匹配所需要的平均时间。表7所示为不同算法在ORL人脸库的特征维数和平均耗时。

表 7. 不同算法在ORL人脸库的特征维数和耗时

Table 7. Dimensionality and time of different algorithms on ORL face dataset

Method	Featuredimensionality	T₁ /ms	T₂ /ms
Wavelet	1920	16.4	14.2
HOG	320	4.5	38.1
Curvelet+PCA+SRC	2850	33.2	41.4
Gabor+HOG	9600	163.3	98.9
NSCT+LBP	3696	856.3	30.1
AWNHOG	2048	15.9	38.3
AWCHOG+KNN	2272	14.5	35.7

查看所有表

由表7可知,在特征维数方面,AWCHOG的特征维数比Gabor+HOG、NSCT+LBP、Curvelet+PCA+SRC要少,同时AWCHOG算法的平均耗时也远小于Gabor+HOG、NSCT+LBP、Curvelet+PCA+SRC和Wavelet 4种算法。采用HOG算子提取人脸图像的梯度幅值和梯度方向特征,需要进行一次反正切运算;Gabor变换会产生5个尺度8个方向的共40个子图,因此需要进行40次高斯卷积运算;采用NSCT分解时会产生11个子图,并且使用LBP还至少需要16个或者59个箱格。Curvelet+PCA+SRC算法则需要对Curvelet变换的4个尺度下所有角度的子图均进行特征提取,会产生较大的维数。而Wavelet算法则要将一幅图像映射到4个子带上。Curvelet系数融合后,AWCHOG就只有4个子图,大大降低了特征的维度,自适应HOG特征提取虽然会在一定程度上增加特征维度,但提取了更加丰富的特征,也提高了识别率。因此AWCHOG算法的识别率要高于对比算法,且其特征维数也更少,单幅人脸图像完成识别的耗时也较少,具有较快的识别速度。

5 结论

提出一种AWCHOG人脸识别算法。该算法利用Curvelet变换提取人脸图像不同尺度、不同方向上的Curvelet系数。为了降低特征维数,提出一种基于实部的编码方式,将不同尺度下不同方向的 Curvelet 系数进行融合,减少了内存的需求以及计算量。由于Curvelet变换无法提取全局特征,因此采用对融合后的图像进行直方图分块的方法来提取特征。针对各个尺度所含的信息量,以及对分类鉴别的贡献率,采用自适应的方式进行加权。实验结果表明,AWCHOG算法不仅在表情、光照、姿势变化以及部分遮挡等方面具有较好的鲁棒性,还在噪声变化方面具有良好的鲁棒性。

参考文献

[1] Shu C, Ding X Q, Fang C. Histogram of the oriented gradient for face recognition[J]. Tsinghua Science and Technology, 2011, 16(2): 216-224.

[2] 杨恢先, 徐唱, 曾金芳, 等. 基于多方向韦伯梯度直方图的人脸识别[J]. 激光与光电子学进展, 2018, 55(11): 111008.

Yang H X, Xu C, Zeng J F, et al. Face recognition based on multi-directional weber gradient histograms[J]. Laser & Optoelectronics Progress, 2018, 55(11): 111008.

[3] 朱小波, 车进. 基于特征融合与子空间学习的行人重识别算法[J]. 激光与光电子学进展, 2019, 56(2): 021503.

Zhu X B, Che J. Person re-identification algorithm based on feature fusion and subspace learning[J]. Laser & Optoelectronics Progress, 2019, 56(2): 021503.

[4] 程超, 达飞鹏, 王辰星, 等. 基于Lucas-Kanade算法的最大Gabor相似度大姿态人脸识别[J]. 光学学报, 2019, 39(7): 0715005.

Cheng C, Da F P, Wang C X, et al. Pose invariant face recognition using maximum Gabor similarity based on Lucas-Kanade algorithm[J]. Acta Optica Sinica, 2019, 39(7): 0715005.

[5] 伍云霞, 张宏. 基于Curvelet变换和压缩感知的煤岩识别方法[J]. 煤炭学报, 2017, 42(5): 1331-1338.

Wu Y X, Zhang H. Recognition method of coal-rock images based on Curvelet transform and compressed sensing[J]. Journal of China Coal Society, 2017, 42(5): 1331-1338.

[6] 李艳萍, 姜颖, 胡金明, 等. 基于曲波变换和余弦测度的人脸识别方法[J]. 计算机科学, 2016, 43(5): 294-297.

Li Y P, Jiang Y, Hu J M, et al. Face recognition method based on Curvelet transform and cosine rules[J]. Computer Science, 2016, 43(5): 294-297.

[7] 周立俭, 刘万泉, 孙洁. 基于Curvelet和LBP的可变光照人脸识别[J]. 计算机工程, 2012, 38(22): 176-178.

Zhou L J, Liu W Q, Sun J. Variable illumination face recognition based on Curvelet and LBP[J]. Computer Engineering, 2012, 38(22): 176-178.

[8] 赵庆敏, 彭雪莹. Curvelet变换结合(2D)2PCA的人脸识别算法[J]. 南昌大学学报(理科版), 2018, 42(2): 180-183.

Zhao Q M, Peng X Y. Research on face recognition based on Curvelet transform and (2D)2PCA[J]. Journal of Nanchang University(Natural Science), 2018, 42(2): 180-183.

[9] Candes EJ, Donoho DL. Curvelet-a surprisingly effective nonadaptive representation for objects with edges[M]. Saint-Malo: Vanderbilt University Press, 1999.

[10] 张志禹, 刘思媛. 一种基于Curv-SAE特征融合的人脸降维和识别方法[J]. 计算机科学, 2018, 45(10): 267-271.

Zhang Z Y, Liu S Y. Method of face recognition and dimension reduction based on Curv-SAE feature fusion[J]. Computer Science, 2018, 45(10): 267-271.

[11] Candes EJ, DemanetL, DonohoD, et al. Fast discrete curvelet transform[R]. Applied and Computational Mathe-matics,California: California Institute of Technology, 2005.

[12] 陈一方, 陈九辉, 郭飚, 等. 接收函数曲波变换去噪与偏移成像[J]. 地球物理学报, 2019, 62(6): 2027-2037.

Chen Y F, Chen J H, Guo B, et al. Denoising the receiver function through curvelet transforming and migration imaging[J]. Chinese Journal of Geophysics, 2019, 62(6): 2027-2037.

[13] 奉俊鹏, 杨恢先, 蔡勇勇, 等. 基于非下采样Contourlet梯度方向直方图的人脸识别[J]. 计算机应用, 2014, 34(1): 158-161.

Feng J P, Yang H X, Cai Y Y, et al. Face recognition based on histograms of nonsubsampled contourlet oriented gradient[J]. Journal of Computer Applications, 2014, 34(1): 158-161.

[14] 周霞, 张鸿杰, 王宪. Shearlet多方向特征融合与加权直方图的人脸识别算法[J]. 光电工程, 2013, 40(11): 89-94.

Zhou X, Zhang H J, Wang X. Face recognition based on Shearlet multi-orientation features fusion and weighted histogram[J]. Opto-Electronic Engineering, 2013, 40(11): 89-94.

[15] 胡丽乔, 仇润鹤. 一种自适应加权HOG特征的人脸识别算法[J]. 计算机工程与应用, 2017, 53(3): 164-168.

Hu L Q, Qiu R H. Face recognition based on adaptively weighted HOG[J]. Computer Engineering and Applications, 2017, 53(3): 164-168.

[16] Déniz O, Bueno G, Salido J, et al. Face recognition using histograms of oriented gradients[J]. Pattern Recognition Letters, 2011, 32(12): 1598-1603.

[17] 杨晋吉, 李亚文. 基于Curvelet变换特征的人脸识别算法[J]. 计算机应用与软件, 2018, 35(1): 169-174.

Yang J J, Li Y W. Face recognition algorithm based on Curvelet transform feature[J]. Computer Applications and Software, 2018, 35(1): 169-174.

[18] 岳许要, 杨恢先, 祝贵, 等. 非采样Contourlet变换与局部二值模式相结合的人脸识别[J]. 计算机应用, 2012, 32(7): 1890-1893.

Yue X Y, Yang H X, Zhu G, et al. Face recognition using nonsubsampled Contourlet transform and local binary pattern[J]. Journal of Computer Applications, 2012, 32(7): 1890-1893.

杨恢先, 李笑笑, 甘伟发. 基于自适应加权Curvelet梯度方向直方图的人脸识别算法[J]. 激光与光电子学进展, 2020, 57(10): 101011. Huixian Yang, Xiaoxiao Li, Weifa Gan. A Face Recognition Algorithm Based on Adaptive Weighted Curvelet Gradient Direction Histogram[J]. Laser & Optoelectronics Progress, 2020, 57(10): 101011.

基于自适应加权Curvelet梯度方向直方图的人脸识别算法 下载： 1171次

1 引言

2 基本原理

2.1 Curvelet变换概述

2.2 HOG

2.3 AWCHOG

表 1. 112 pixel×92 pixel人脸图像经过Curvelet变换后的系数形式

Table 1. Form of Curvelet coefficients after Curvelet transform for 112 pixel×92 pixel face image

图 1. 四个尺度融合图像。(a)尺度1;(b)尺度2;(c)尺度3;(d)尺度4

Fig. 1. Fusion images at four scales. (a) Scale 1; (b) scale 2; (c) scale 3; (d) scale 4

3 AWCHOG算法的人脸识别

3.1 AWCHOG特征提取

3.2 人脸匹配

4 实验结果与分析

图 2. AWCHOG算法流程图

Fig. 2. Flow of AWCHOG algorithm

图 3. ORL人脸库。(a)图像1;(b)图像2;(c)图像3;(d)图像4;(e)图像5;(f)图像6

Fig. 3. ORL face dataset. (a) Image 1; (b) image 2; (c) image 3; (d) image 4; (e) image 5; (f) image 6

图 4. AR人脸库。 (a)训练样本;(b)表情集;(c)光照集;(d)遮挡集A;(e)遮挡集B

Fig. 4. AR face dataset. (a) Training sample; (b) facial express subset; (c) illumination subset; (d) partial occlusion subset A; (e) partial occlusion subset B

图 5. CAS-PEAL人脸库。 (a)训练样本; (b)表情集; (c)背景集; (d)饰物集

Fig. 5. CAS-PEAL face dataset. (a) Training sample; (b) Express subset; (c) Background subset; (d) Accessory subset

4.1 参数对实验效果的影响

表 2. Curvelet变换不同尺度下的识别率

Table 2. Recognition rate of Curvelet transform at different scales

图 6. ORL人脸库在不同梯度方向数下的识别率

Fig. 6. Recognition rate of ORL face dataset at different gradient directions

4.2 与其他算法识别率对比

图 7. ORL人脸库不同尺度在不同分块方式下的识别率。(a) Coarse层;(b) detail 1层;(c) detail 2层;(d) fine层

Fig. 7. Recognition rate of ORL face dataset in different block modes. (a) Coarse floor; (b) detail 1 floor; (c) detail 2 floor; (d) fine floor

表 3. ORL人脸库上的识别率

Table 3. Recognition rate on ORL database

表 4. CAS-PEAL人脸库上的识别率

Table 4. Recognition rate on CAS-PEAL database

表 5. AR人脸库上的识别率

Table 5. Recognition rate on AR database

4.3 加噪实验

表 6. 加入高斯噪声后,AR光照库上不同算法的实验结果

Table 6. Results of different algorithms on AR illumination subset after adding Gaussian noise

4.4 算法复杂度分析

表 7. 不同算法在ORL人脸库的特征维数和耗时

Table 7. Dimensionality and time of different algorithms on ORL face dataset

5 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于自适应加权Curvelet梯度方向直方图的人脸识别算法下载： 1171次