0 引　言

随着太空技术的发展，空间非合作目标的高精度探测、跟瞄及对接等技术受到国内外研究机构的广泛重视^[1-2]。激光成像雷达通过发射高重频激光脉冲并接收其散射信号，快速构建目标三维轮廓，是开展此类任务的重要光电载荷。已报道的空间三维成像雷达主要依赖于单元或线列推扫式，其优势在于灵活的视场配置和较高的点云密度，由于扫描速率限制，在开展动态平台或非合作目标观测时，其测量结果与实际轮廓存在较大差异^[3-4]。近年来，基于阵列传感器的非扫描激光雷达正在成为国内外三维成像领域的研究热点^[5-6]。基于高灵敏度APD阵列的面阵激光雷达，可实现单脉冲瞬时成像，有效解决了运动扫描导致的时间同步问题和条带错位现象^[7]。受限于像元规模，当视场有效重叠面积较小，或目标存在自遮挡时，其点云数据将变得稀疏，呈现出交替变形的分布特征。此外，阵列探测器内部像元串扰特性引起的边缘模糊现象，也对在轨点云处理带来了较大挑战^[8]。因此，有必要研究面向典型非合作目标、具有鲁棒性的空间面阵多视角点云配准算法进行位姿测量。

目前，工业界点云配准方法主要由粗配准和精配准两个阶段组成。粗配准方法基于随机一致性采样思想，通过建立关键点对或特征描述符，降低随机匹配过程的运算量，例如快速点特征直方图^[9]（Fast Point Feature Histograms, FPFH）、视点特征直方图^[10]、3D形状上下文特征^[11]等信息。此外，包括主成分分析^[12]（Principal Component Analysis, PCA）、四元数法^[13]、正态分布变换^[14]（Normal Distribution Transform, NDT）等方法也展现出粗配准能力。在此基础上，Mellado等人针对四元数法运算时效进行了改进，提出了使用智能索引将计算复杂度从 $ o\left({n}^{2}\right) $降低到 $ o\left(n\right) $的Super-4PCS配准框架^[15]。Brenner等人提出基于迭代种子的区域生长法面特征对点云进行配准^[16]。精配准方法以迭代最近点算法（Iterative Closest Points, ICP）为代表^[17]。为了扩大初始值收敛范围，更高效率的ICP变体方法包括将点对点配准推广到单对多、多尺度迭代、点面结合等方式^[18-19]，降低了精配准的耗时量。近年来，在三维重建和SLAM等领域也出现了一些高效的点集配准算法。Fitzgibbon等人综合高斯牛顿法和梯度法的优势，根据误差函数的当前值与极小值的距离调整参数，提出了可快速收敛的Levenberg-Marquardt 迭代最近点方法^[20]。Jacopo等人利用点周围3D结构间的关联特性，开发了稳健的NICP配准框架^[21]。Charles等人提出了基于学习的PointNet深度配准算法，通过大规模训练点云网络，避免了手动推导复杂点云结构框架^[22]。Zhang等人在多维点集相干点漂移基础上，将其推广到包含各项异性噪声时的点集配准，并给出了迭代闭合解^[23]。Zang等人提出了一种密度自适应的相干点漂移方法，通过约束概率模型内的几何特征进行配准优化^[24]。

针对空间非合作目标阵列成像点云特性，文中提出了一种改进相干点漂移算法对位姿测量中相邻帧点云进行配准。在单次源点云漂移后，对点集之间的距离残差进行排序，根据重叠比率得到参与运算的最优变换点云对，对迭代参量增加局部扰动量，并在迭代过程中引入重叠测度对权值因子进行自适应调整。此外，为避免陷入局部最优点，对均方误差更新率进行监督，通过变换点集属性提高鲁棒性，降低初始位姿差异较大时的误配准现象。最后，通过建立两种典型空间非合作目标多视角阵列成像工况，验证了所采用配准算法的精确度和鲁棒性。

1 配准方法与原理

1.1 面阵点云配准问题分析

基于二维焦平面阵列的激光成像雷达通过测量各像元回波的光子飞行时间，实现非扫描全视场同步成像。设接收视场角为 $ \alpha $，阵列规模为 $ {p}^{2} $，像元 $ \left(m,n\right) $的深度为 $ d $，则水平夹角 $ {\theta }_{x} $为 $ m\alpha /p $，同理 $ {\theta }_{y} $。根据空间几何映射关系，其对应点云坐标 $ (x,y,z) $为：

$ D=(z\cdot \tan{\theta }_{x},z\cdot \tan{\theta }_{y},\sqrt{{d}^{2}/({\tan}^{2}{\theta }_{x}+{\tan}^{2}{\theta }_{y}+1)}) $ (1)

由于不同视角下的面阵点云轮廓具有较大差异，为了建立其位姿变换关系，需要对相邻帧阵列点云配准。其映射关系由旋转矩阵 $ R $和平移向量 $ T $所组成的刚性变换矢量 $ H $表征。设参考点云为 $ {P}_{t} $，待配准点云为 $ {P}_{s} $，变换点云 ${{P}_{s}}'$为 $ {R}_{3\times 3}{P}_{s}+{T}_{3\times 1} $。配准目的是构建坐标点对集合，使得点集 $ {P}_{s} $在最佳变换矢量 $ {H}^{*} $下，跟点集 $ {P}_{t} $之间的误差函数值最小，其本质为凸优化问题：

$ H({R}^{*},{T}^{*}) =\underset{R,T}{\mathrm{a}\mathrm{r}\mathrm{g}{\rm{min}}}\frac{1}{\left|{P}_{s}\right|}\sum _{i=1}^{\left|{P}_{s}\right|}{\left|\right|{p}_{t}^{i}-(R{p}_{s}^{i}+T)\left|\right|}^{2} $ (2)

即min[ $ H(R,T) $]下的解 $ (R,T) $为最优变换矩阵。通过固定一组旋转平移矩阵 $ (R,T) $，利用基于KD-tree或八叉树的最邻近算法，找到最优点对 $ \{{p}_{t}^{i};{p}_{s}^{i}\} $；然后固定该最优点对 $ \{{p}_{t}^{i};{p}_{s}^{i}\} $，对旋转平移矩阵 $ (R,T) $优化，其收敛依据为公式(2)中代价值H下降至极小值。然而，当点云初始位姿偏差过大或存在非重叠冗余噪点时，容易出现误配准。针对文中配准场合，典型空间非合作目标由帆板面、矩体及柱舱等部件组成，焦平面阵列易受到空间背景辐射和探测器串扰影响，经滤波去噪等预处理后，实际点云精度和确信度均有所下降，对在轨配准应用算法提出了挑战。

1.2 基于改进的相干点漂移配准方法

相干点漂移方法是一种基于全局概率拓扑的多维数据点集匹配算法，不仅适用二维图像的拼接，也可用于三维点云的刚性/非刚性配准，在图像融合、影像匹配等领域展现出较强的鲁棒性^[25]。它通过计算点云在GMM模型下的负对数似然函数，将点集之间的映射作为概率分布关系而求解。

1.2.1 点云相干点漂移的配准原理

基于相干点漂移配准方法将多维空间点集最优匹配问题视作为混合高斯分布模型下概率密度参数的估计问题。为了避免变换点集属性混淆，对点集定义予以区分，设参考点集为 $ X=\{{x}_{1}, {x}_{2},\cdots,{x}_{N}\} $，待配准点集为 $ Y=\{{y}_{1},{y}_{2},\cdots,{y}_{M}\} $，待配准变换为 $ \tau (Y,\theta ) $。在每次迭代中，点集 $ Y $将被视作为质心点集，即 $ {y}_{m} $构成混合高斯模型GMM中单个分量，而点集 $ X $则是GMM生成的观测数据集。为了降低冗余噪点的影响，施加权重为 $ w $的均匀分布成份。因此，点 $ {x}_{n} $的分布概率为：

$ \widehat{P}\left({x}_{n}\right)=(1-w)\sum _{m=1}^{M}\widehat{P}\left({y}_{m}\right)\widehat{p}\left({x}_{n}\right|{y}_{m})+w\frac{1}{N} $ (3)

式中： $ \widehat{P}\left({y}_{m}\right)=1/M $，即各个高斯分量概率相同。当点集 $ Y $中先验点为 $ {y}_{m} $时，组成GMM模型的单个高斯参量基函数可以表示为：

$ \widehat{p}\left({x}_{n}\right|{y}_{m})=\frac{1}{{\left(2\pi {\sigma }^{2}\right)}^{D/2}} \Bigg /{\rm{{\rm{exp}}}}\left(-\frac{{\left|\right|{x}_{n}-{y}_{m}\left|\right|}^{2}}{2{\sigma }^{2}}\right) $ (4)

式中： $ {\left|\right|{x}_{n}-{y}_{m}\left|\right|}$为点 $ {x}_{n} $与 $ {y}_{m} $的欧式距离。为求解最优变换对 $ \tau (Y,\theta ) $，在每次迭代过程中，通过最大化点集 $ X $内数据点的似然函数：

$ L\left(\theta ,{\sigma }^{2}\right)=\prod _{n=1}^{N}\widehat{P}\left({x}_{n}\right)=\prod _{n=1}^{N}\sum _{m=1}^{M+1}\widehat{P}\left({y}_{m}\right)\widehat{p}\left({x}_{n}\right|{y}_{m}) $ (5)

两边同取对数后，即极小化负对数似然函数：

$ E\left(\theta ,{\sigma }^{2}\right)={\rm{log}}\left(L\left(\theta ,{\sigma }^{2}\right)\right)=\sum _{n=1}^{N}{\rm{log}}\sum _{m=1}^{M+1}\widehat{P}\left({y}_{m}\right)\widehat{p}\left({x}_{n}\right|{y}_{m}) $ (6)

由于集合 $ \theta $内包括旋转 $ R $、平移 $ t $等参量，难以直接进行求导，因此采用期望极大化方法，构建该似然函数解析式，不断进行期望步（E step）和极大步（M step）迭代，求解最佳参数变换对。

1.2.2 文中的自适应配准算法流程

相干点漂移对重叠度及噪声特性等有较高要求，当相对初始位姿差异较大时算法易陷入失能。本节针对空间非合作目标阵列点云，基于相干点漂移方法收敛特性，对每次漂移后源点云使用局部空间最近邻估计方法进行正向推测，并通过反刚性变换调整点云姿态。对迭代后的点云对，监督均方误差更新率直至陷入局部值，依次交替待源点云与目标点云的属性，跳出局部最优变换矩阵，提高全局配准收敛性。配准流程如图1所示，其主要步骤如下：

图 1. 文中针对空间阵列点云的自适应改进相干点漂移配准算法流程图

Fig. 1. Diagram of the proposed adaptive CPD registration strategy for spatial planar-array-based point clouds

下载图片 查看所有图片

（1）对目标点云 $ {P}_{t} $与源点云 $ {P}_{s} $预处理，将各坐标分量(x,y,z)归一化，计算GMM模型初始方差 $ {\sigma }^{2} $：

$ {\sigma }^{2}=\frac{1}{3\left|{P}_{t}\right|\left|{P}_{s}\right|}\sum _{n}^{\left|{P}_{t}\right|}\sum _{m}^{\left|{P}_{s}\right|}{\left|\right|{p}_{t}^{n}-{p}_{s}^{m}\left|\right|}^{2} $ (7)

（2）根据贝叶斯公式，利用初始方差计算混合高斯模型下点集 $ {P}_{t} $~ $ {P}_{s} $的后验概率，即：

$ \widehat{p}\left({P}_{s}\right|{P}_{t})=\frac{\widehat{p}\left({P}_{s}\right)×\widehat{p}\left({P}_{t}\right|{P}_{s})}{\displaystyle{\sum} _{m=1}^{\left|{P}_{s}\right|+1}\widehat{p}\left({p}_{s}^{m}\right)×\widehat{p}\left({P}_{t}\right|{p}_{s}^{m})} $ (8)

根据公式(3)和公式(4)，可以得到：

$ \begin{split} &\widehat{p}\left({P}_{s}\right|{P}_{t})=\\ &\frac{{\rm{exp}}\left(-\dfrac{{\left|\right|{p}_{t}-{p}_{s}\left|\right|}^{2}}{2{\sigma }^{2}}\right)}{\displaystyle{\sum} _{m=1}^{\left|{P}_{s}\right|}{\rm{exp}}\left(-\dfrac{{\left|\right|{p}_{t}-{p}_{s}^{m}\left|\right|}^{2}}{2{\sigma }^{2}}\right)+\dfrac{w}{1-w}\times \dfrac{\left|{P}_{s}\right|}{\left|{P}_{t}\right|}\times {\left(2\pi {\sigma }^{2}\right)}^{\tfrac{3}{2}}} \end{split} $ (9)

针对式中权重 $ w $，为提高配准自适应性，引入最大公共点集测度（Largetst Common Pointset, LCP）作为迭代过程中的重叠特性追踪因子，其定义为：

$ \delta ={N}_{s}^{r}/\left|{P}_{s}\right| $ (10)

式中： $ \left|{P}_{s}\right| $为点云 $ {P}_{s} $的规模，建立变换后点云 $ {P}_{s} $的查找表，对点云 $ {P}_{t} $中进行容差半径为 $ r $的邻域搜索； $ {N}_{s}^{r} $为邻域元素长度非 $ 0 $的点对数量。对于待配准点云，单次迭代后非匹配点集的权值为：

$ w=1-{\delta }^{2} $ (11)

当迭代过程中权值 $ w $更新速率低于阈值时，将前次迭代的容差半径乘以惩罚系数 $ \alpha $，作为其测度搜索范围 $ r $，使得当源点云向目标点云逼近过程中，参与漂移配准的运算点比例进行自适应调整。

（3）根据凸函数Jesson不等式，GMM模型负对数似然函数 $ L\left(\theta ,{\sigma }^{2}\right) $的下界Q函数可表示为：

$ Q(\boldsymbol{\theta },{\sigma }^{2})=\sum _{n=1}^{N}\sum _{m=1}^{M+1}{\widehat{P}}^{old}\left({p}_{s}^{m}\right|{p}_{t}^{n}\left)\log\right[{\widehat{P}}^{new}\left({p}_{s}^{m}\right){\widehat{P}}^{new}\left({p}_{t}^{n}\right|{p}_{s}^{m}\left)\right] $ (12)

对该式进行简化，最终得到：

$ \begin{split} &Q(\boldsymbol{\theta },{\sigma }^{2})=\\ &\frac{1}{{2\sigma }^{2}}\sum _{m,n=1}^{M,N}{d}_{m,n}{\widehat{P}}^{old}\left({p}_{s}^{m}\right|{p}_{t}^{n})+\frac{3}{2}\log{\sigma }^{2}\sum _{m,n=1}^{M,N}{\widehat{P}}^{old}\left({p}_{s}^{m}\right|{p}_{t}^{n}) \end{split} $ (13)

其中 $ {d}_{m,n} $表示点云 $ {P}_{t} $与更新点云 $ {P}_{s} $的欧式距离：

$ {d}_{m,n}={\left|\right|{p}_{t}^{n}-\tau ({p}_{s}^{m},\theta )\left|\right|}^{2}={\left|\right|{p}_{t}^{n}-s\boldsymbol{R}{p}_{s}^{m}-t\left|\right|}^{2} $ (14)

该步骤的求解依赖于EM算法^[25]，其求解过程使得该下界值最大化，等效于最大化GMM模型的似然函数，得到最佳参数对 $\theta (\boldsymbol{R}',t',s)$。然而，当两片点云重叠性较低时，非匹配点云构成的观测数据对高斯分布模型估计带来较大偏差，造成 $ \theta $无法收敛至所需精度。采用最近邻估计对迭代参量 $ \theta $增加局部扰动量。将每次迭代所得源点云 $ \tau ({P}_{s},\theta ) $，根据初始归一化系数得到单次迭代时的更新点集 ${P}_{s}'$。计算每次迭代后的重叠系数，不断剔除距离值过大的点对从而进行正向推测。该过程首先建立更新点集 ${P}_{s}'$的KD-tree，搜索其每个点离点集 $ {P}_{t} $的最近邻点，计算这些最近邻点对的距离 $ {d}_{i}^{2} $并将其进行排序，选择前K个点对，得到其距离和 $ s\left({d}_{i}^{2}\right) $。其中，单次迭代的所需点对数量为：

$ K=\delta ×\left|{P}_{s}\right| $ (15)

对于所选点对 $\{{p'}_{t}^{1},\cdots,{p'}_{t}^{K}\}$和 $\{{p'}_{s}^{1},\cdots,{p'}_{s}^{K}\}$，根据期望最大化方法，计算使公式(2)最小化时的最佳变换 $ ({R}^{*},{T}^{*}) $。假设两点集的质心分别为 $\overline{{p'}_{t}}$、 $\overline{{p'}_{s}}$，对其构成的协方差矩阵 ${\boldsymbol H}$进行SVD奇异值分解：

$ {\boldsymbol H}=U\varSigma {V}^{{\rm{T}}}=\sum _{i=1}^{K}({p'}_{si}-\overline{{p'}_{s}}){({p'}_{ti}-\overline{{p'}_{t}})}^{{\rm{T}}} $ (16)

其最优旋转变换矩阵和平移向量为：

$ {\boldsymbol{R}}^{*}=V{U}^{{\rm{T}}},{t}^{*}=\overline{{p'}_{t}}-{\boldsymbol{R}}^{*}\overline{{p'}_{s}} $ (17)

（4）上述步骤中单次迭代的空间变换参量为：

$ \boldsymbol{R}=s{\boldsymbol{R}}^{*}{\boldsymbol{R}}',t={\boldsymbol{R}}^{*}{t}'+\frac{1}{c}{t}^{*} $ (18)

所得的更新点集为：

$ {P}_{s}^{ud}=s{\boldsymbol{R}}^{*}{\boldsymbol{R}}'{P}_{s}^{now}+{\boldsymbol{R}}^{*}{t}'+\frac{1}{c}{t}^{*} $ (19)

通过不断迭代求解，直至两点云之间 $ s\left({d}_{i}^{2}\right)/K $小于阈值或迭代次数达到设定值时，则停止循环。根据质心及缩放参数对其反归一化为标准点云。

（5）考虑到初始位姿差异过大可能导致运行时迅速陷入局部值，使 $ \tau (Y,\theta ) $提前结束寻优过程。在此，通过监督配准误差的收敛情况，当陷入局部最优估计时，对数据点集 $ X $与GMM质心点集 $ Y $的属性行交替迭代：在初始运算阶段，将待配准点云 $ {P}_{s} $作为高斯混合模型的质心点集 $ X $，而参考点云 $ {P}_{t} $作为其数据分布集 $ Y $。当均方差值更新幅度低于阈值时，在参考点云 $ {P}_{t} $作为质心点集 $ X $的同时，将移动点云 $ {P}_{s} $作为数据点集 $ Y $。该方法在点云特性差异较大时，提高了收敛概率。在交替点集属性后，执行步骤(1)~(4)，通过空间反旋转平移变换求解最终点云。设最优变换对为 $ (\boldsymbol{R}',t') $，则变换后点云可表示为：

$ {P}_{s}={\boldsymbol{R}'}^{-1}{P}_{s}^{ud}-\boldsymbol{R}'t' $ (20)

在初始位姿差异较大，特别是待配准点云内非重合点比率较大时，耗时量有所增加，而鲁棒性明显提升。图2(a)为该算法运行过程中配准误差随着迭代次数的收敛曲线，相比于标准相干点漂移方法，其单次迭代过程中收敛程度具有显著提升。如图2(b)所示，当GMM模型参数求解陷于局部值时，该算法具有跳出局部解并实现收敛的能力。

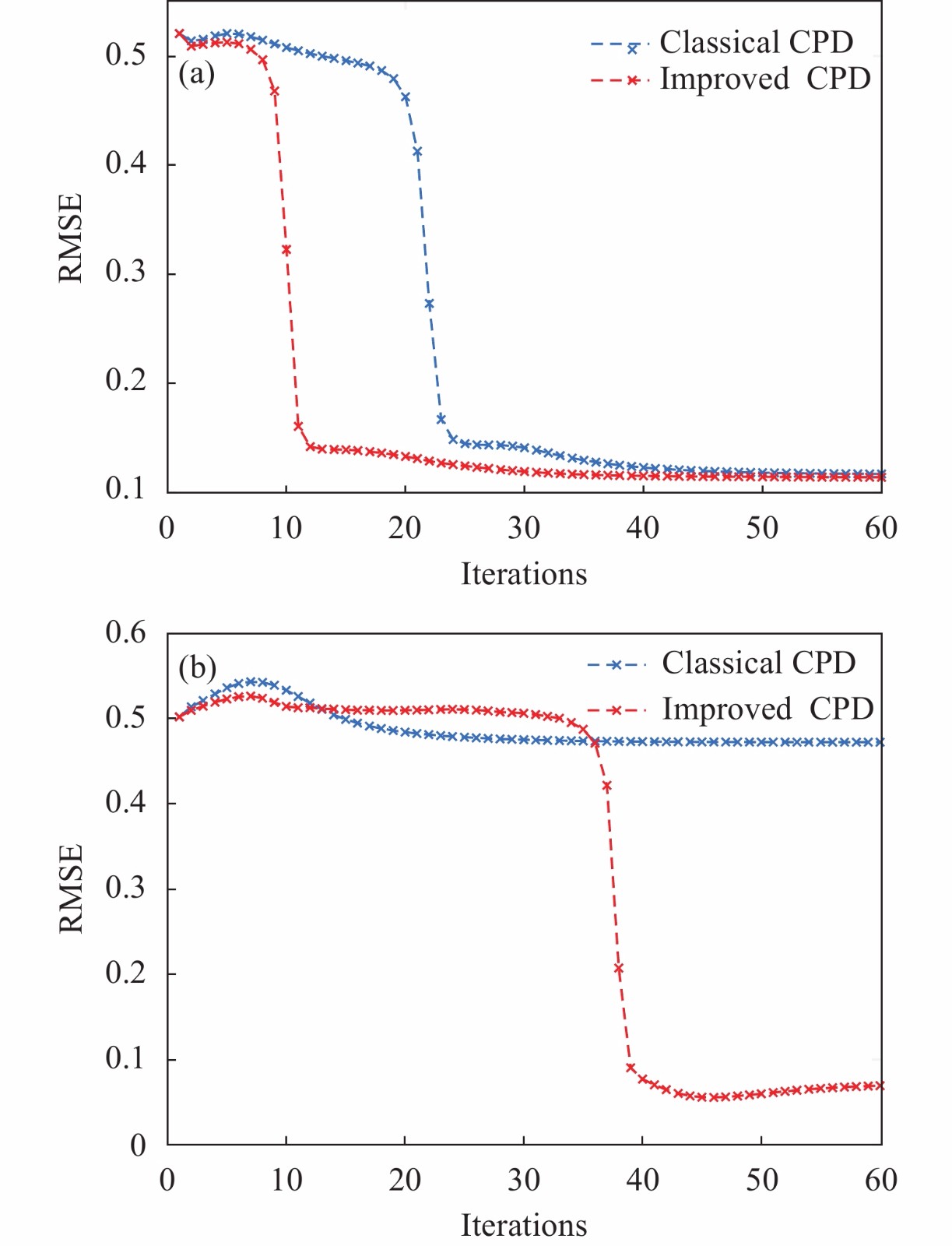
图 2. (a) 均方误差随迭代次数的变化； (b) 陷入局部值后的收敛曲线

Fig. 2. (a) Variation of RMSE with the iterations ; (b) Convergence curve of RMSE under local minimum

下载图片 查看所有图片

2 试验分析与讨论

空间非合作目标运动主要由绕自旋轴和绕进动轴的两个旋转分量决定，采用环绕伴飞或进动等方式可获得不同视角的轮廓。为明确文中研究目的，即位姿测量中不同视角阵列点云拼接配准问题，对此类目标低姿态分量加以简化，建立多视角空间探测仿真工况。采用组合式粗+精配准算法作为对比，结合文中改进相干点漂移方法，对所采集的不同工况下空间非合作目标阵列式点云进行配准验证。

为了定量化评价匹配结果，采用LCP测度（重叠系数）及RMSE均方误差这两个常用指标作为衡量最终配准效果的依据。LCP定义如上节所述，即对变换后点云 $ {P}_{s} $中某个点，在容差范围内存在任意点云 $ {P}_{t} $中点则认为是重合点，其比例为LCP测度，容差 $ r $为0.05。此外，定义均方误差为：

$ RMSE=sqrt\left[\frac{1}{\left|{P}_{s}\right|}\sum _{i=1}^{\left|{P}_{s}\right|}{({p}_{s}^{i}-{\widetilde{p}}_{t}^{i})}^{2}\right] $ (21)

式中： $ {p}_{s}^{i} $为配准后的源点云，规模为 $ \left|{P}_{s}\right| $，其内部各点离目标点云 $ {P}_{t} $最近的点为 ${\widetilde{p}}_{t}^{i}$。通常而言，若配准方法使得变换后的源点云RMSE相对差异较小时，当其LCP测度越大，则配准效果越好。

2.1 空间非合作目标面阵成像点云仿真工况

结合当前大规模盖格/线性APD焦平面阵列的研制进展，仿真像元规模为 $ 128\times 128 $，视场约为 $ 3{\text{°}}\times 3{\text{°}} $。为了更清晰地反映相邻待配准点云之间的关系，采用相邻两帧点云在本体坐标系下的视角差 $ \Delta \varphi $和相对距离 $ R $作为自变量。文中仿真过程中主要考虑到以下两种典型的简化后空间探测工况：

（1）成像平台环绕以某姿态分量不断变化的卫星目标进行全视角采集。在近似圆周运动下，假设平台运动的线速率为 $ v $，此时系统的成像帧频可表示为：

$ F=\frac{v}{\Delta \varphi *R} $ (22)

采用某卫星三维模型，其外接矩体包围框约 $ 1.8\;\mathrm{m}\times 4.8\;\mathrm{m}\times 1.9\;\mathrm{m} $。如图3所示，探测距离为80 m， $ Z $轴姿态角在90°~180°之间连续地变换，平台绕 $ Y $轴采集相邻视角差为10°的点云数据。在该数据集内按指定视角间距大小选取待配准点云，验证系统在不同成像帧频下的配准效果。

（2）成像平台向非合作目标连续进动。目标的 $ X $轴姿态分量不断变换，该场景下点云具有分布密度不一致、平移分量差异大等特性。如图3所示，探测目标绕 $ X $轴转动，载荷平台从90 m进动至40 m，数据集中相邻探测间隔为10 m，其不同帧点云之间具有较大的视角差异性。

在空间探测场景下，受环境背景噪声、探测器串扰以及时间测量板的量化精度等因素影响，焦平面测距值无法达到绝对仿真距离。主要包括两点：一是实际点云通常以随机偏差分布在绝对真实值点云的周围；二是尽管多数离散噪点可以通过体素滤波等进行预处理，但环境背景及串扰导致的边缘模糊，使得分布在正确点云周围的噪点无法有效滤除，并参与配准运算。因此，需要对以上两种仿真工况下得到的绝对点云进行退化，约束其精度及信噪比。

假设激光脉冲波形及探测器内部响应造成的系统误差呈高斯分布，在绝对点云的各个维度上，加入均值为理论值，标准差 $ \sigma $为 $ 0.005 $的扰动量，即：

$ {p}_{x,y,z}'={p}_{x,y,z}+{\varepsilon }_{x,y,z},f\left(\varepsilon \right)=\frac{1}{\sigma \sqrt{2\pi }}{\rm{exp}}\left[-0.5\cdot {\left(\frac{\varepsilon }{\sigma }\right)}^{2}\right. $ (24)

式中： $ {p}_{x,y,z}' $为输出点云； $ {p}_{x,y,z} $为绝对值；各维度偏差量为 $ {\varepsilon }_{x,y,z} $；服从概率密度为 $ f\left(\varepsilon \right) $的高斯分布。

此外，针对面阵探测器的串扰模糊效应，对上述步骤处理后的含噪点云，按照指定比率将选定点周围点集进行随机替换：坐标点集规模为 $ N $，近距离随机噪点比率为 $ \sigma $，选取 $ \sigma N $个随机点，寻找并计算其周围 $ k $点的均值并替换。该实验中仿真点云中模糊比率 $ \sigma $为 $ 0.2 $，噪点周围均值统计点数 $ k $为10。图4(a)和(b)分别为某视角下的绝对仿真点云和退化后待配准点云，逼近真实探测场景的情况。

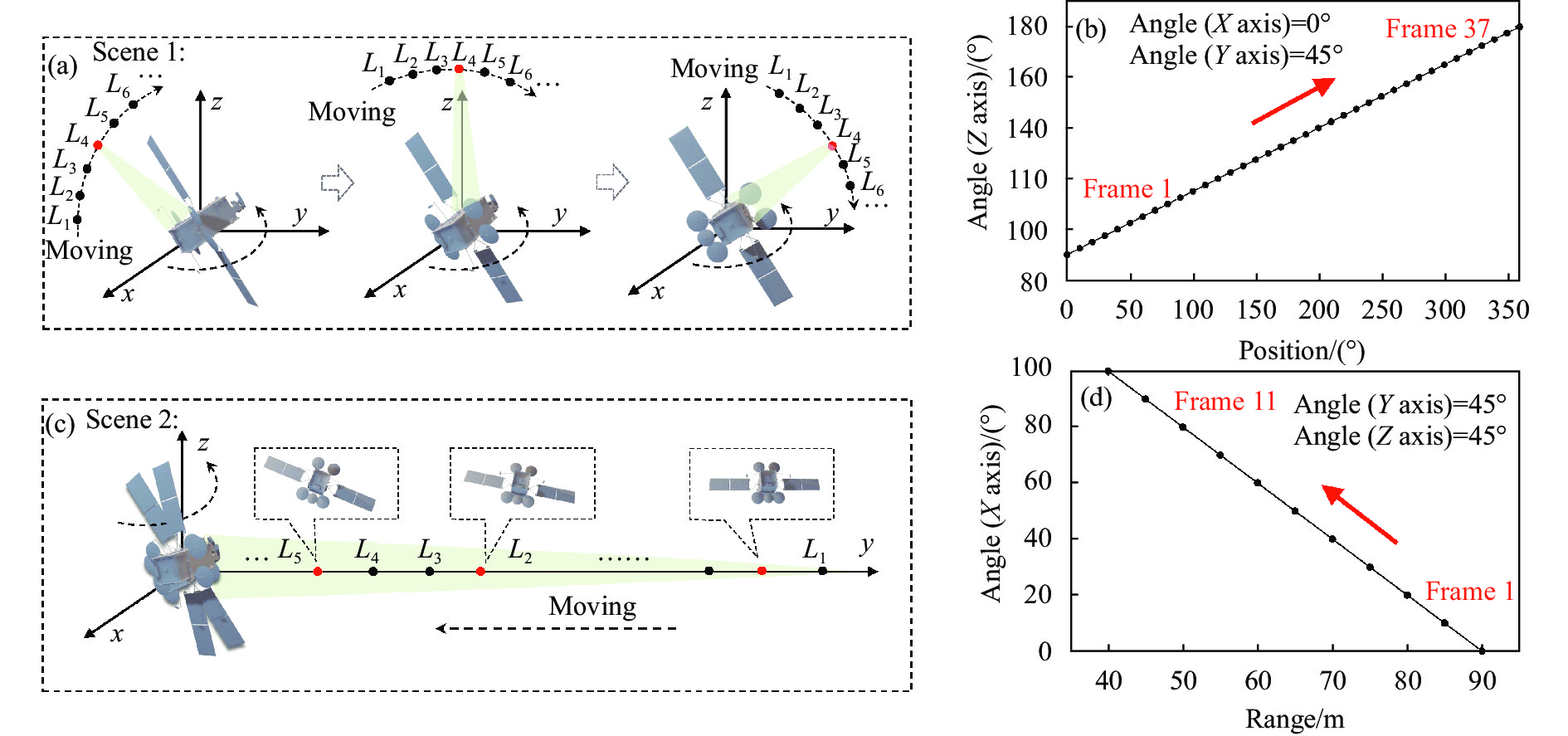
图 3. (a) 工况1：成像平台围绕80 m处目标Y轴旋转，卫星绕Z轴运动；(b)为目标姿态与观测角对应关系；(c) 工况2：成像平台沿Y轴自90 m处到40 m处进动，卫星绕X轴运动；(d)为目标姿态与探测距离的对应曲线

Fig. 3. (a) Case 1: The platform rotates around the Yaxis of the 80 m target, and the satellite moves around the Zaxis; (b) is the correspondence between the target attitude and the observation angle; (c) Case 2: The platform moves along the Yaxis from 90 m to 40 m, and the satellite moves around the Xaxis; (d) is the link between the target attitude and the detection distance

下载图片 查看所有图片

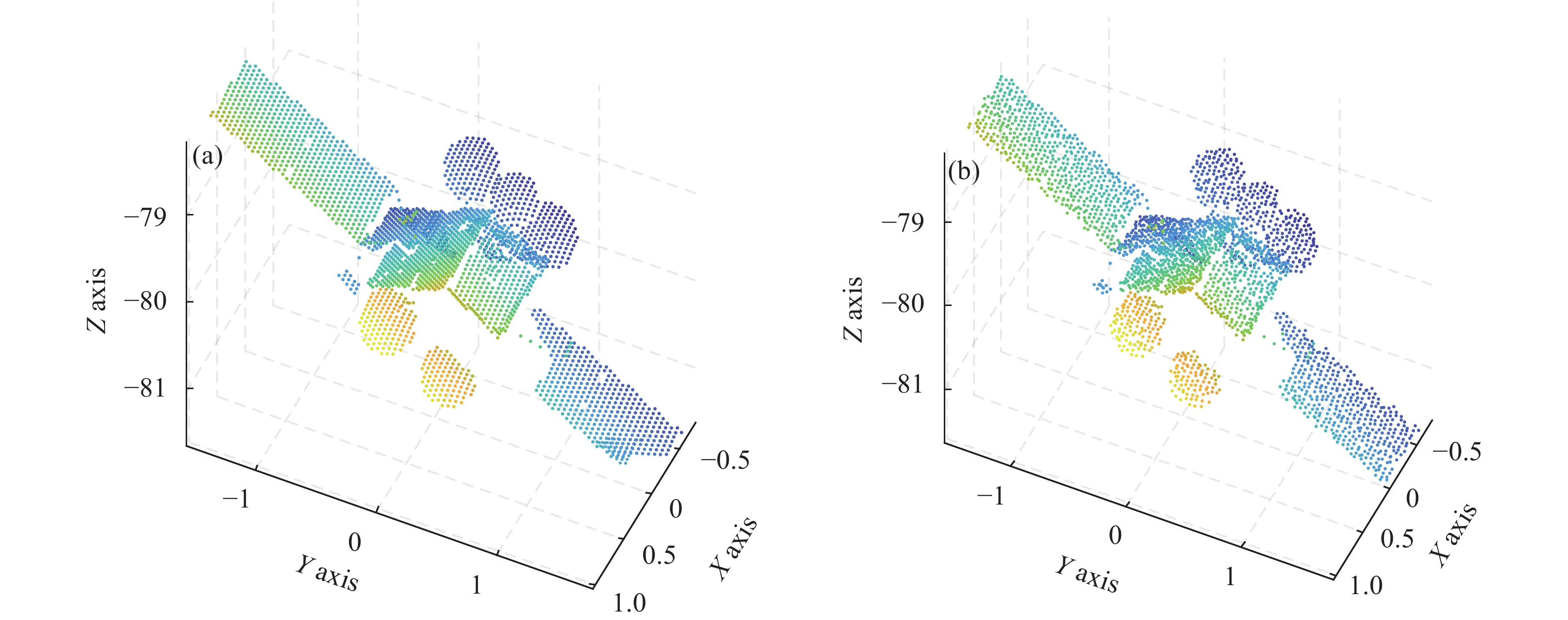
图 4. (a) 某姿态角下绝对仿真点云； (b)含有噪声扰动的退化仿真点云

Fig. 4. (a) Absolute simulation point cloud at a certain pose; (b) Degraded simulation point cloud with noise perturbation

下载图片 查看所有图片

2.2 两种工况下算法配准效果验证及讨论

为了验证算法性能，使用以上含噪仿真数据集进行配准分析。对于初始位姿差异较大的点云，直接使用ICP方法极易陷入局部最小值，导致配准结果可靠性较差。因此本节分别采用基于FPFH特征匹配的随机采样一致性SAC算法、基于正态分布变换算法和基于主成分分析方法的初始粗配准算法，结合ICP方法进行精配准，以及文中方法，对指定相邻帧点云进行配准分析。

原始点云的初始位姿差异大小是检验鲁棒性的重要因素。对于工况1，相邻两帧待配准点云间姿态差异由系统成像帧频决定，反映于成像平台绕目标的观测角。图5所示为初始状态下相邻观测角间隔 $ \Delta \theta $为90°（即 $ {\theta }_{1}=0{\text{°}},{\theta }_{2}=90{\text{°}} $）时的配准结果。如表1所示，由于多数点邻域的特征近似，基于FPFH特征的SAC配准方法在此类空间矩体轮廓下的匹配误差较大，其粗配和精配的RMSE分别为0.651和0.174，其ICP精配准过程陷入了局部值。NDT算法不需要对点云进行特征计算及匹配，计算速度相对较快，通过将离散点云分为多个块状网格来计算分布参数，在该类维度信息不规整的空间非合作目标下的映射关系难以收敛，因此未能取得预期配准效果。

对于PCA+ICP方法而言，正适用于此类主成分分量明显的目标，其初始配准的LCP测度和RMSE分别为32%和0.131。需要注意，由于PCA方法对各主轴方向具有极性两向性，因此不同场合下对ICP精配的初始输入姿态差异较大，导致精配过程中可能朝错误方向收敛。针对文中的优化相干点漂移方法，相对PCA+ICP配准算法而言，在RMSE近似相同的情况下的耗时量略有提高，重叠度提升了约9%，在后续相邻帧连续配准实验中，其匹配可靠性优势较显著。

图 5. 在工况1下相邻帧点云的视角差为90°时配准结果： (a) SAC+ICP； (b) NDT+ICP； (c) PCA+ICP； (d) 文中方法

Fig. 5. Registration results when the difference between the viewing angles of adjacent point cloud is 90 °under Case 1: (a) SAC+ ICP; (b) NDT + ICP; (c) PCA + ICP; (d) Proposed method

下载图片 查看所有图片

此外，针对工况1数据集，指定绕飞成像帧频使得相邻待配准点云帧视角差 $ \Delta \varphi $分别为30°和60°，进行连续配准试验。图6中，文中配准方法在相邻视角差为30°时，随着成像平台的不断运动，LCP测度在0.75~0.95之间呈现出交替变换，符合目标姿态及观测角不断调整时的点云特性规律。其余方法的重叠度和RMSE均呈现出较大幅度振荡，并出现了不同程度地误配准，具有较低鲁棒性。

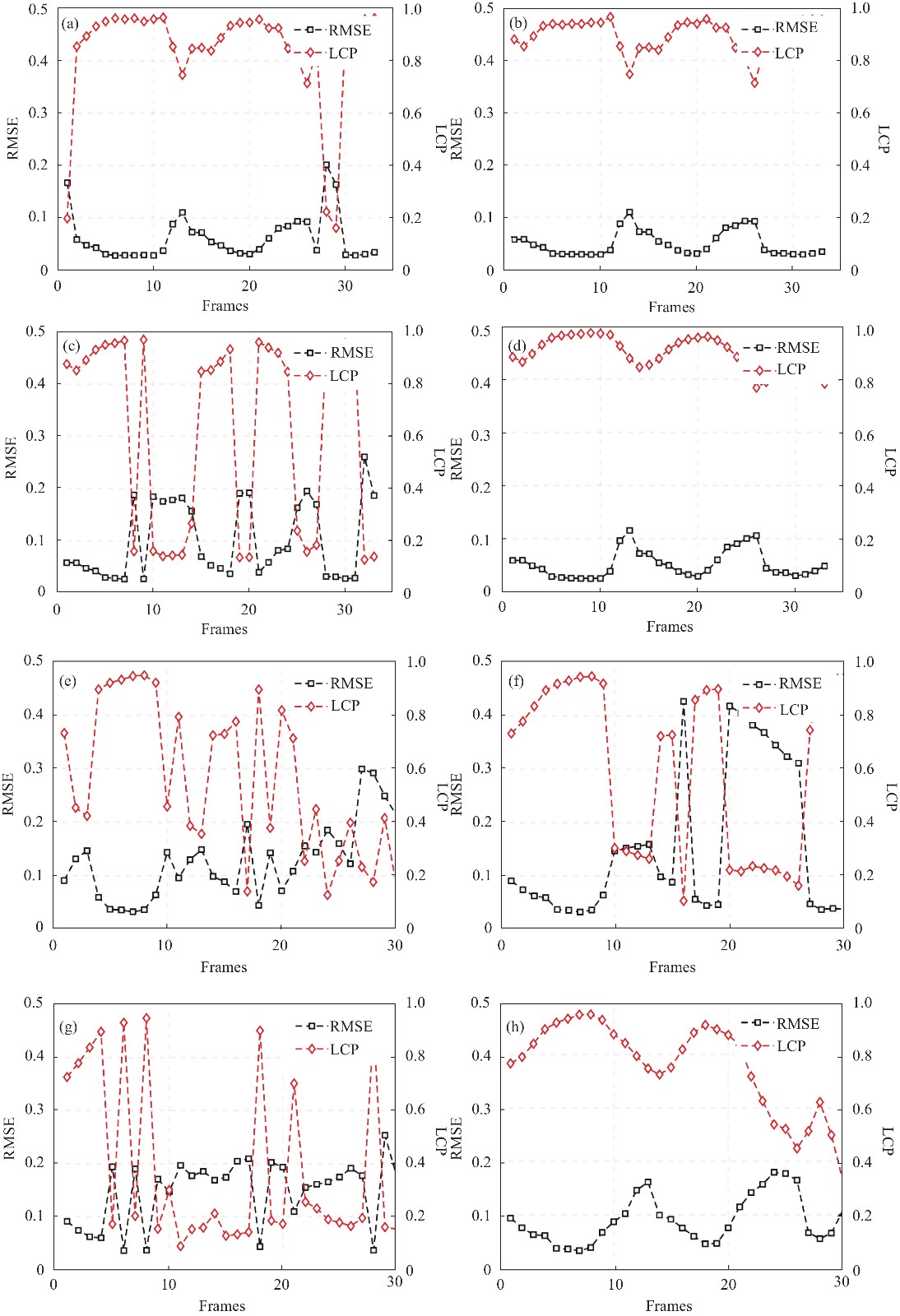
图 6. 工况1下相邻点云帧视角差为30°和60°时的连续配准：(a)~(d)对应于30°视角差时的两两配准结果，分别为SAC+ICP、NDT+ICP、PCA+ICP以及文中的配准方法，同理(e)~(f)对应于60°视角差下的配准结果

Fig. 6. Registration results when the viewing angle difference is 30° and 60° in Case 1: (a)-(d) are the results of SAC+ICP, NDT+ICP, PCA+ICP and the proposed method when the viewing angle difference is 30°. Similarly, (e)-(f) correspond to the 60° viewing angle difference

下载图片 查看所有图片

在工况2下，相邻待配准点云之间的差异不仅体现在不断变化的目标姿态上，其重叠度和分布密度也随探测距离的降低而产生差异。图7(a)为探测距离为90 m和60 m时的待配准点云，两者相对于X轴位姿差为60°。图7(b)~(e)及表2分别为以上配准框架的结果。该视角下点云所含特征信息量较大，基于特征匹配的方法表现出了较强的配准能力，其重叠度和RMSE分别达到了58.8%和0.105，但耗时量有所增加。对于主成分分析方法，极性模糊造成的姿态差异过大使得精配准中出现误配准现象。文中的改进相干点漂移算法在耗时量和RMSE上，相对SAC+ICP方法较高，其重叠度提升了约34%，从图(b)和图(e)的配准结果可以看到，两种方法配准结果的重叠度具有明显提升。

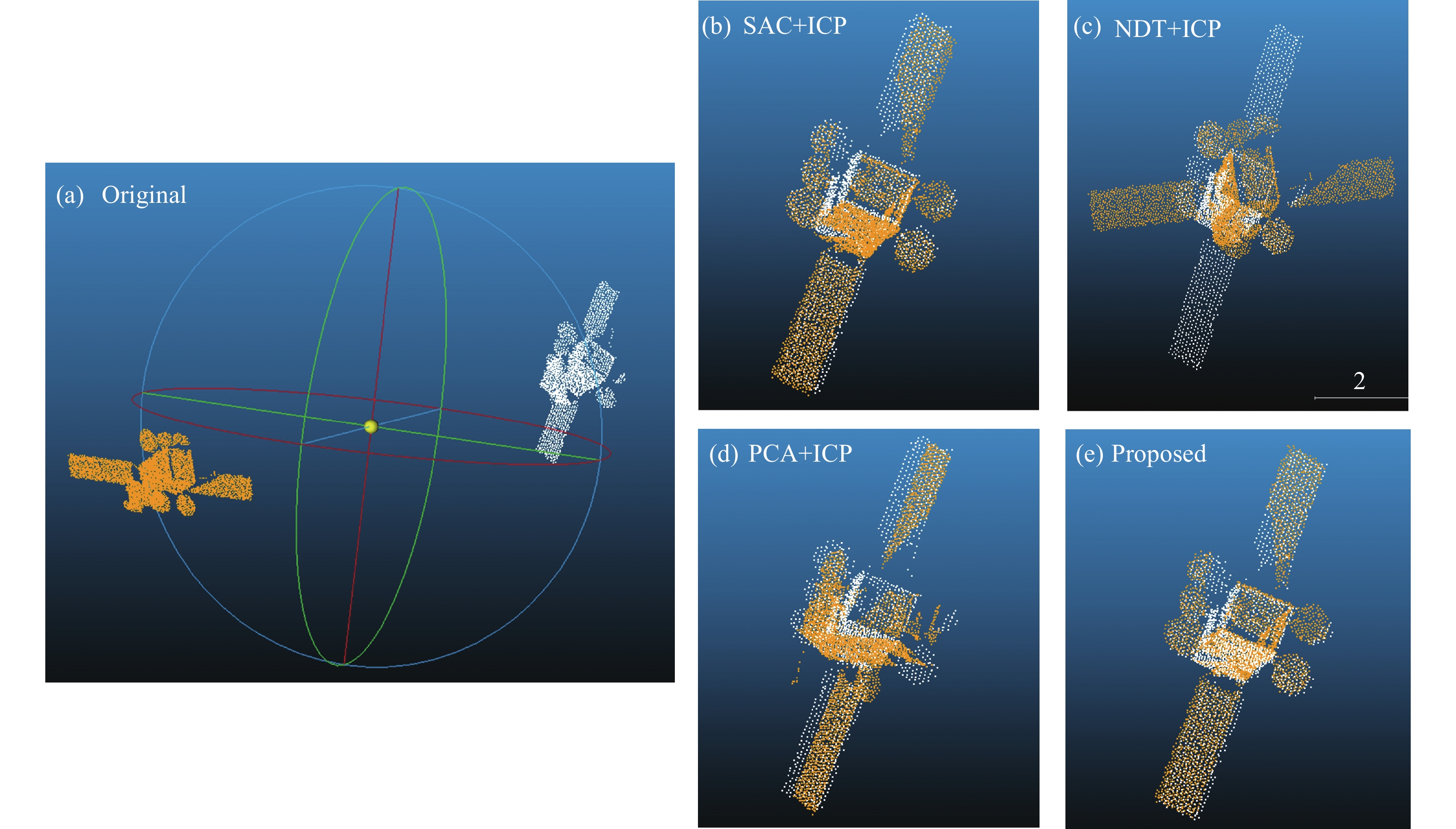
图 7. 在工况2下相邻点云距离为30 m时的配准结果：(a)初始位姿； (b) SAC+ICP； (c) NDT+ICP ；(d) PCA+ICP； (e)文中方法

Fig. 7. Registration results when the distance between adjacent point cloud is 30 m under Case 2: (a) Initial position; (b) SAC + ICP; (c) NDT + ICP; (d) PCA + ICP; (e) Proposed method

下载图片 查看所有图片

此外，仍然采用相邻两帧点云连续相互配准的方式对算法进行测试。为了使点云间差异更加直观，采用相邻点云的距离间隔作为衡量依据。在距离差分别为10 m （X轴视角差为20°）和20 m （X轴视角差为40°）时，使用上述方法进行配准，其结果如图8所示。由此可以看出，文中方法在均方误差以及重叠度上均表现出较稳定的变化趋势，其结果可靠性优于其他粗+精组合配准方法。

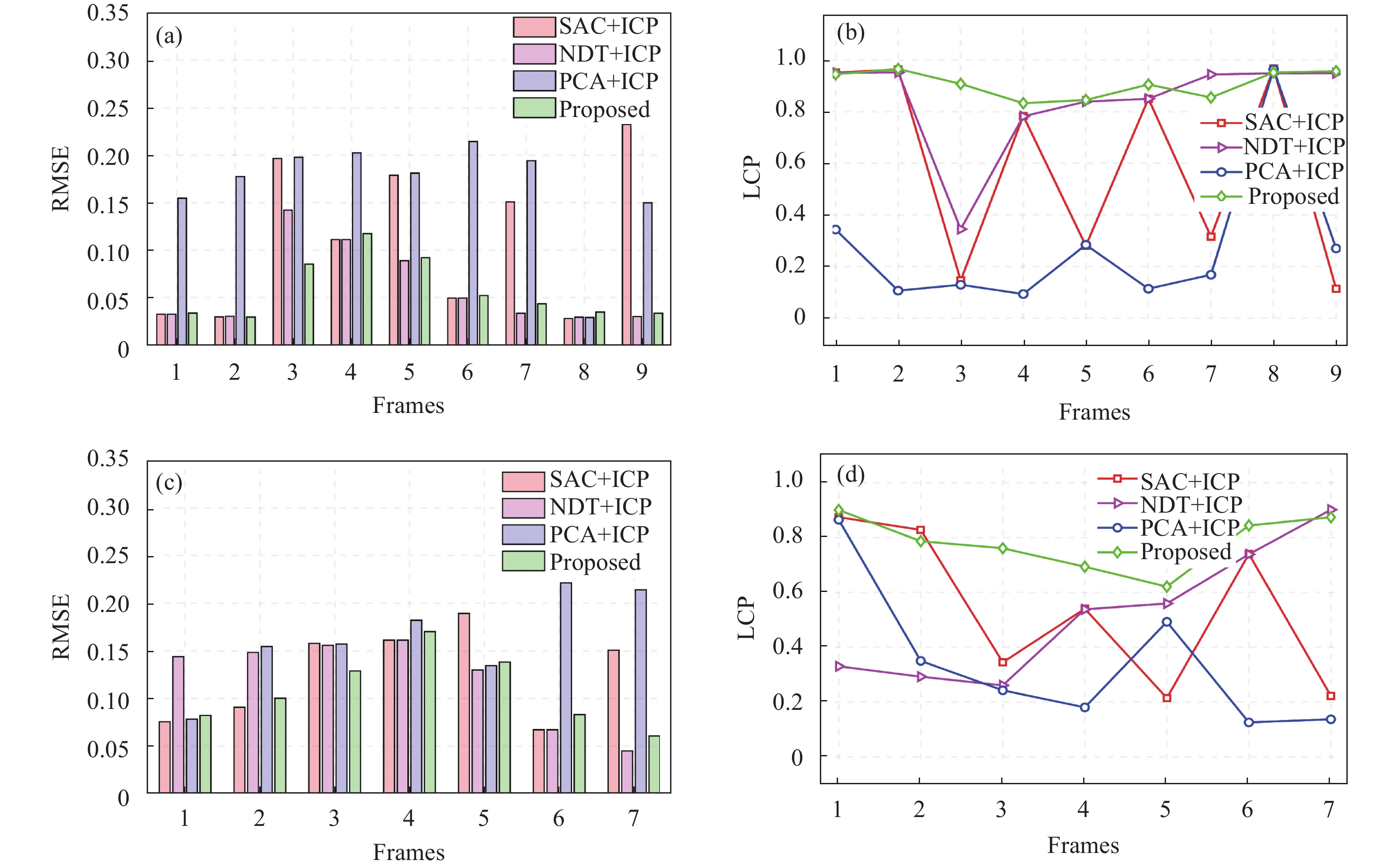
图 8.

Fig. 8. Continuous registration results for the point cloud with the distance difference between adjacent frames of 10 m and 20 m in Case 2: (a)-(b) corresponds to ∆d=10 m, (c)-(d) corresponds to ∆d=20 m 工况2下点云相邻帧距离差为10 m和20 m时的连续配准结果：(a)~(b)对应于 10 m，(c)~(d) 对应于 20 m

下载图片 查看所有图片

2.3 强背景噪声扰动下的算法鲁棒性验证

考虑到在真实空间探测场景中存在情况：受某些背景辐射源的影响造成点云信噪比过低；焦平面阵列或激光器性能裂化，使得光电探测能力随着载荷服务时长出现不同程度地下降，导致点云数据变得稀疏。本节针对该类极限扰动场景下点云进行仿真与配准验证。 采用上节工况2中探测距离为90 m的仿真数据作为目标点云，源点云为平台向前进动30 m后，待配准点云相对X轴的视角差为60度。在原退化点云的噪声基础上，依次叠加标准差 $ \sigma $为0.02和0.05的扰动量、比率 $ \tau $为0.5和0.8的近距离随机噪点，其定义如2.1节所述。取上述试验中结果相对可靠的三种配准方法：基于特征匹配的SAC+ICP框架、基于主成分分析+ICP精配准以及文中相干点漂移方法，其配准结果评价指标如表3所示。

从图9可以看到，前面两种配准框架在点云数据质量发生剧烈下降后，均出现了不同程度的误配准，特别是噪声标准差 $ \sigma $变大，其结果将受到显著影响。对于文中方法，其平均RMSE和LCP测度相对其他两种方法分别提升了约6%和61%，连续配准时的结果具有明显的鲁棒性优势。在不同噪声分布特性下，该优化方法完成了多视角点云的配准任务，具有较强的抗噪声干扰能力。

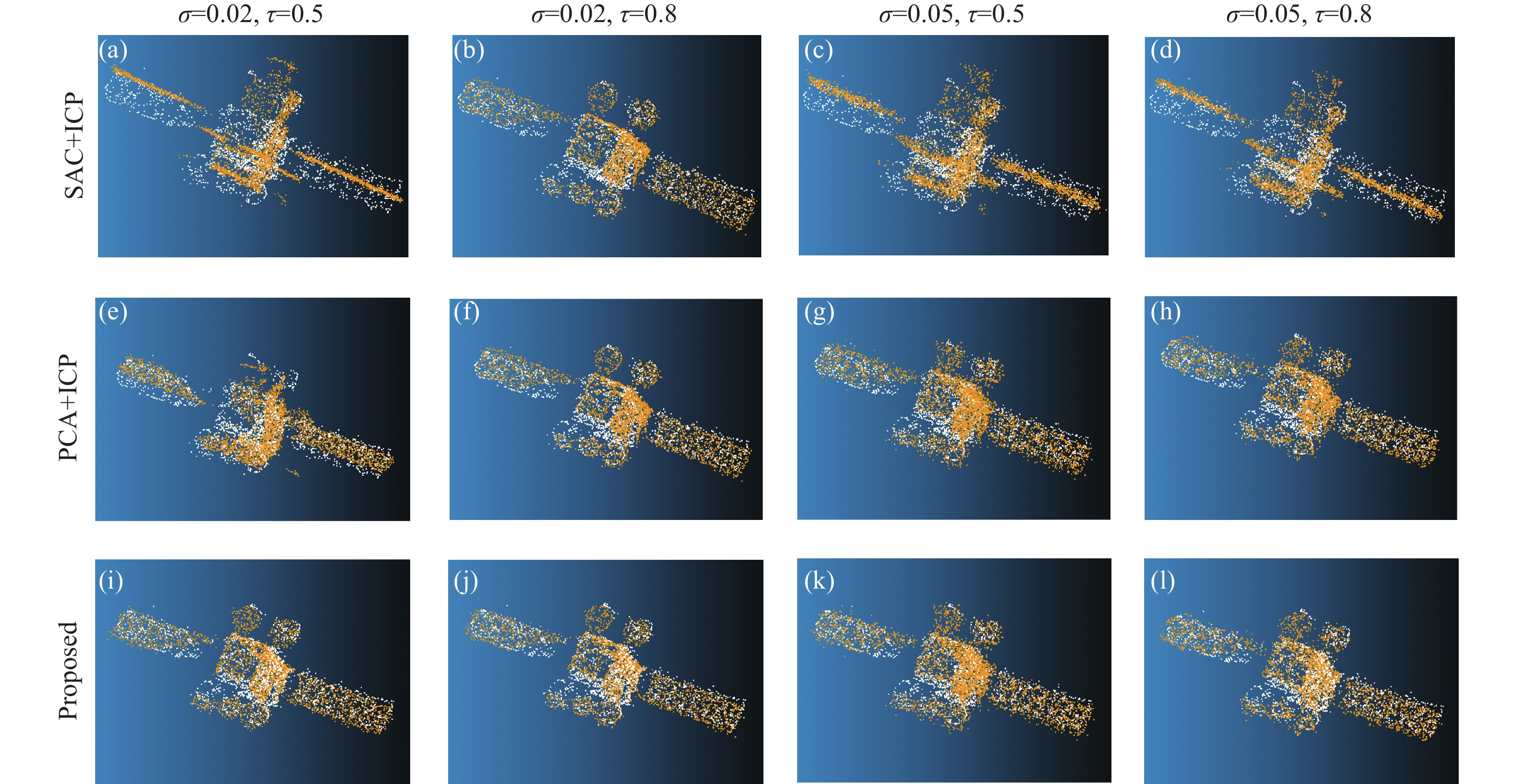
图 9. 在强噪声干扰情况下的点云配准结果：(a)~(d)为SAC+ICP框架在不同噪声水平下的配准结果； (e)~(h)为PCA+ICP框架；(i)~(l)为对应于文中配准算法的配准结果

Fig. 9. Registration results under extreme strong noise : (a) - (d) are the results of SAC-ICP framework under different noise level; (e)-(h) is PCA + ICP; (i) - (l) Correspond to the registration method in this paper

下载图片 查看所有图片

3 结　论

面阵激光雷达可以有效地解决空间探测场景下运动导致的距离同步问题，文中针对空间位姿测量任务，提出了一种改进相干点漂移方法对空间非合作目标阵列点云进行配准。通过建立简化后的空间运动目标面阵三维成像仿真工况，得到不同视角的阵列点云，验证了该配准算法的精度和可靠性。

在空间探测应用中，阵列式点云相对于推扫点云而言，更容易受到视场配置引起的背景噪声干扰。试验结果表明，即使在受到不同程度及特性的噪声干扰情况下，该方法仍然可以准确地完成配准任务，其结果优于包括特征匹配、正态分布以及主成分分析等粗+精配准组合框架。此外，对于地面或其它廓线特性差异较大的配准目标，仍需深入地考虑系统成像特性、探测目标几何特征及匹配指标等因素，综合不同算法框架的优势来解决多视角点云配准问题。后续工作将致力于该配准方法的轻量化实现及运算资源优化问题，对片上移植的实时性及动态范围等指标着重关注。