基于里德堡原子外差传感器的宽带高灵敏探测  下载: 1570次特邀研究论文【增强内容出版】
下载: 1570次特邀研究论文【增强内容出版】
Rydberg atoms became increasingly crucial in the last decade because of their fascinating characteristics that distinguish them from conventional radio frequency (RF) sensors. First, the Rydberg atoms are self-calibrating thanks to the invariance of the atomic parameters, and their response is linked to Plank's constant. Second, atomic sensing systems break a key assumption behind the Chu limit of traditional electronic sensors by allowing a small vapor cell to operate over multiple octaves of frequencies from DC to THz. Third, instead of demodulated circuitry, Rydberg atoms can naturally extract the baseband signals from the carrier frequency. Fourth, Rydberg atoms may avoid internal thermal (Johnson) noise, even at room temperature. In recent years, the amazing introduction of the local oscillator (LO) RF field has assisted us in controlling ensembles of Rydberg atoms. However, most current reports on Rydberg atomic heterodyne sensors focus on measurements in the resonant region, which can only achieve highly sensitive detection at discrete frequencies due to the quantum nature of the atomic energy level. In this work, by extending the Rydberg atomic heterodyne technique from the resonant region to the off-resonant region, we experimentally validated the continuous broadband and high sensing sensitivity of Rydberg atoms.
When a strong LO field and a weak signal (SIG) field with frequency detuning on the order of kHz are irradiated to the atoms, the energy level will be modulated by the intermediate frequency (IF) in the resonant and off-resonant regions, which can be directly detected by optical electromagnetically induced transparency (EIT). At room temperature, a probe laser of 852 nm and a coupling laser of 509 nm propagate in opposite directions and overlap inside a 2 cm-long vapor cell containing cesium atoms, exciting the atoms to the Rydberg state for atomic sensing. In the resonant region, the LO frequency is set to 2.63 GHz, and the SIG frequency is set to 2.63 GHz+10 kHz. Both fields are illuminated into the vapor cell by a horn antenna 7 cm away from the optical path, and the polarization of the two RF fields is the same as that of the probe and coupling beams and propagates in a vertical direction to the laser beams. While in the off-resonant region, the frequencies of the LO and SIG fields are tuned to 300 MHz and 300 MHz+10 kHz, respectively. An aluminum parallel-plate waveguide serves as the microwave transmitter in the off-resonant region. The reflection coefficient (S11) of the input port is below -20 dB from DC to 850 MHz (Fig. 2), indicating the excellent port matching performance of the parallel-plate waveguide.
In the resonant region, we calibrated the electric (E) field strength of the RF field using the Autler-Townes (AT) splitting effect. By adjusting the output power of the signal generator to satisfy the linear relationship between AT-splitting and RF field amplitude, we obtained the relationship between the square root of the signal generator output power and the E-field intensity calculated by AT-splitting (Fig. 3). The results show excellent linearity, and the weak RF E-field strength can be inferred from the fit line. Then, a spectrum analyzer was used to measure the intensity of the beat-note signal under Rydberg atomic heterodyne conditions. We measured a series of data points of the beat-note signal strength versus the applied SIG power (Fig. 4). The intensity of the received beat-note signal is approximately proportional to the strength of the applied SIG field with a linear dynamic range of over 45 dB. The minimum SIG output power is -85 dBm, which is limited by the background noise of the spectrum analyzer. By leveraging the gradient of the fit line, we can obtain the minimal detectable E-field of 220.94 nV/cm, with the corresponding sensing sensitivity of -131.9 (dBm/cm2)/Hz. Similarly, in the off-resonant region, through the relationship between the power injected in the parallel-plate waveguide and the E-field strength, we measured the minimum E-field strength of 19 μV/cm in the off-resonant region at 300 MHz, with a sensitivity of -93.2 (dBm/cm2)/Hz. Besides, we also measured the instantaneous bandwidth of the system in the off-resonant region (Fig. 5). By taking into account the negative detuning of the SIG and LO fields, the instantaneous bandwidth of 3 dB of the system reaches 90 kHz.
In the present study, two typical frequency points in the resonant and off-resonant regions were selected to experimentally verify the broadband and high sensitivity detection capability of Rydberg atomic sensors. During the measurement, a horn antenna and a parallel-plate waveguide were used as microwave transmitters in the resonant and off-resonant regions, respectively. Using the Rydberg atomic heterodyne technique, we successfully measured a minimum E-field strength of 220.94 nV/cm with a sensitivity of -131.9 (dBm/cm2)/Hz in the resonant region at 2.63 GHz and a minimum E-field strength of 19 μV/cm with a sensitivity of -93.2 (dBm/cm2)/Hz in the off-resonant region at 300 MHz, respectively. In principle, by adjusting the laser frequency to excite the alkali metal atoms to various Rydberg states and incorporating the distinct responses of Rydberg atoms to E-fields in the resonant and off-resonant regions, highly sensitive sensing of microwave E-fields can be achieved in the broadband continuous spectral range.
1 引言
里德堡原子是指主量子数(n)很大的高激发态原子,拥有极大的极化率(n7)和微波跃迁偶极矩(n2),对外部电磁场非常敏感,极易受外场调控。利用电磁诱导透明(EIT)效应可以将外部电磁场对里德堡原子能级的扰动转换为光谱的变化,实现宽带电磁频段的全光无损探测。里德堡原子作为一种新型的量子微波测量手段,相比于传统电子学测量方法,有许多独特的优势:1)可溯源、自校准。里德堡原子的测量结果可以追溯至基本物理常数(普朗克常数)[1],此外,原子的能级间隔不随外部环境的变化而改变,因此,里德堡原子具有自校准的优势;2)可实现超宽带、无扰测量。传统电子学传感器利用金属结构中电子在外部电磁场作用下的受激运动实现对待测微波场的测量,其物理尺寸受限于Chu[2]极限,需要根据待测微波场的波长而改变。而里德堡原子的能级间隔处于微波波段,利用一个填充碱金属原子的厘米量级的玻璃气室,就可以实现千赫兹至太赫兹的超宽带频率范围内的全光无损探测;3)对调制信号的自动解调能力。不同于传统电子学接收机,里德堡原子可以将待测调制场中的基带信号直接解调出来,而无需复杂的解调电路[3-4];4)有望突破电子学接收机的灵敏度极限。在常温下,利用低熵激光探测外部电磁场对里德堡能级的扰动可以免受电子热噪声的困扰,有望实现更高的测量灵敏度。
自2012年Shaffer团队[5]利用微波耦合相邻里德堡能级产生的Autler-Townes(AT)分裂效应在实验上实现微波电场强度测量以来,各研究团队相继报道了多种方法提高里德堡原子的电场测量灵敏度。例如,利用再泵浦激光提高基态可作用原子数[6],利用三光子激发手段克服原子运动引起的多普勒失配[7-8],通过外加辅助微波场来缀饰相邻里德堡原子能级[9-11],以及利用谐振增强结构提高原子作用处场强[12-14]等。上述方法大都基于里德堡原子谐振区的AT分裂效应和非谐振区的ac Stark偏移效应对电场强度进行直接测量,侧重于通过压窄EIT线宽以获得更高的光谱分辨率的方式提高电场测量灵敏度。而在常温下,受原子热运动的影响,EIT的线宽很难压窄至3 MHz以下,这限制了里德堡原子电场测量灵敏度的进一步提升。
2019年,研究者们开发了一种里德堡原子外差方法来提升电场测量灵敏度[15-16]。通过添加一个频率与待测微波电场频率相差千赫兹量级的强本振微波场来提升里德堡原子对微弱信号的感知能力,在本振微波场的作用下,EIT光谱呈现正弦调制,调制频率为本振微波信号与待测微波信号的差频频率。相比于AT分裂法和ac Stark偏移法等直接测量手段,里德堡原子外差方法可以将电场测量灵敏度提升2~3个数量级[17-18],极大地提升了里德堡原子的探测能力。然而,现有关于里德堡原子外差的文献大多针对谐振区探测[15-18],由于原子能级的量子化特性,谐振区外差只能实现离散频点的高灵敏探测,并不能满足宽带频谱的连续测量。
本文以一个2 cm长的室温铯原子气室作为传感器,利用里德堡原子外差法分别实验测量了谐振区2.63 GHz处最小场强为220.94 nV/cm和非谐振区300 MHz处最小场强为19 μV/cm的微波弱信号,电场测量灵敏度分别达到
2 里德堡原子谐振区与非谐振区的电场响应
当外加微波电场的频率等于两个里德堡能级的跃迁频率时,原子的能级和光谱会发生分裂,称为谐振区响应;当外加微波电场的频率不满足两个里德堡能级的跃迁频率时,原子的能级和光谱会发生移动,称为非谐振区响应。
2.1 谐振区响应
在谐振区,外加的微波电场通过耦合相邻里德堡能级使得原子光谱发生EIT-AT分裂现象,电场强度E与AT分裂间隔∆AT之间存在线性对应关系[19]:
式中:
在里德堡原子外差条件下,待测信号场和强本振场可以分别表示为
结合
2.2 非谐振区响应
在非谐振区,里德堡原子的能级和光谱会在外加微波电场的作用下发生ac Stark偏移,电场强度E与光谱偏移量∆Stark之间呈二次方对应关系[21]:
式中,α为里德堡原子的动态标量极化率。
在非谐振区,里德堡原子变为一种二次方传感器。在里德堡原子外差条件下,由于
结合
3 实验装置
里德堡原子外差法测电场的实验装置及相应的双光子跃迁阶梯EIT能级如图

图 1. 实验装置与能级示意图。(a)实验装置图;(b)双光子跃迁阶梯里德堡EIT能级示意图。Ωp和Ωc分别表示探测光和耦合光的拉比频率
Fig. 1. Experimental setup and energy-level diagram. (a) Diagram of experimental setup; (b) diagram of two-photon transition ladder Rydberg EIT energy levels, where Ωp and Ωc are probe and coupling Rabi frequencies, respectively
本振场及信号场通过相位同步的两个微波信号源产生,并通过一个功率合成器输送给不同的微波发射装置。对于谐振区探测,2.63 GHz的本振信号和(2.63 GHz+10 kHz)的待测信号共同馈入喇叭天线,天线口面距离原子气室7 cm,辐射方向与激光传播方向垂直且微波极化方向与激光偏振方向一致。对于非谐振区探测,将本振信号和待测信号分别调谐至300 MHz和(300 MHz+10 kHz),用平行板波导[25]作为微波辐射装置,平行板波导实物及非谐振区实验场景如
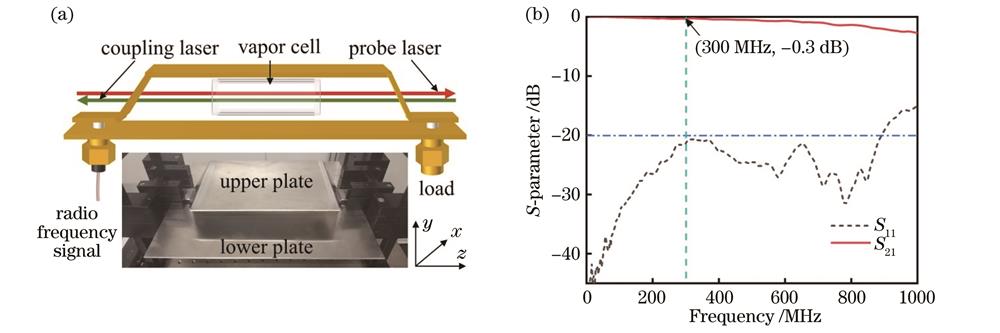
图 2. 平行板波导及其S参数测试曲线。(a)平行板波导实物及非谐振区实验示意图。原子气室放置于平行板波导上下极板中间,激光从通光孔照射进原子气室;(b)平行板波导S参数测试曲线。300 MHz处的插入损耗为0.3 dB
Fig. 2. Parallel-plate waveguide and its S-parameter test curve. (a) Parallel-plate waveguide physical object and its experimental sketch in off-resonant region. Vapor cell is placed in center between upper and lower plates of parallel-plate waveguide, and lasers are incident into vapor cell through optical apertures; (b) parallel-plate waveguide S-parameter test curve. Insertion loss is 0.3 dB at 300 MHz
4 实验结果与讨论
4.1 谐振区测量
为了获得准确的里德堡原子电场测量灵敏度,首先需要对空间辐射电场进行校准。利用里德堡原子自校准的优势可以获得不同发射功率下原子作用位置处的准确电场值。校准时,只开启本振信号源。2.63 GHz的微波信号会引起64D5/2态和65P3/2态之间的共振跃迁,造成EIT光谱的分裂,根据
以AT分裂间距为媒介,实验测量了不同信号源输出功率的开方值与所对应的原子作用处电场强度的关系如
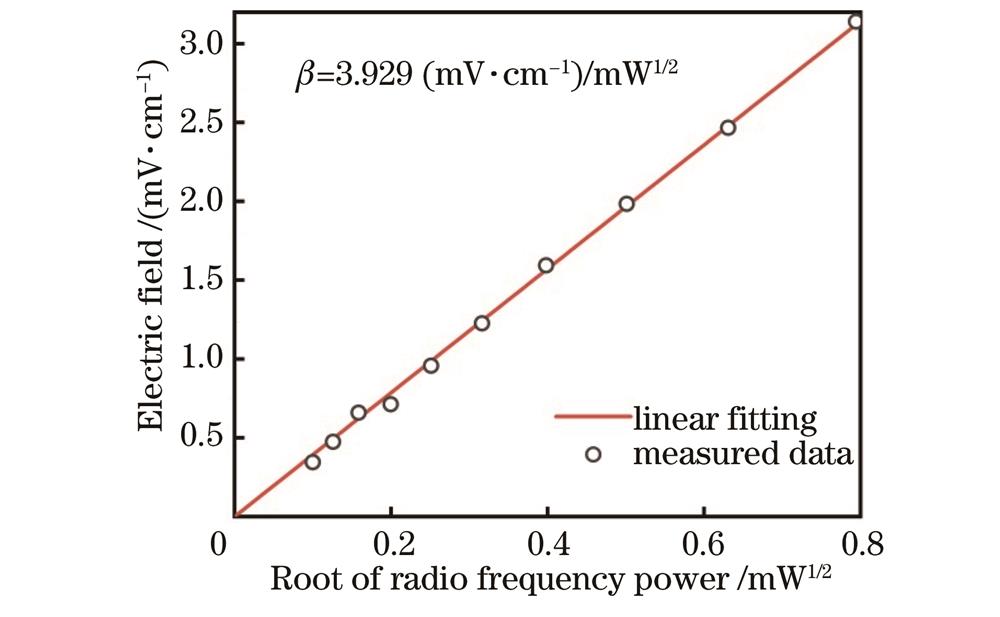
图 3. 通过EIT-AT光谱测量的射频电场(空心圆点)与待测信号源输出功率平方根的关系,以及其与3.929(mV·cm-1)/mW1/2梯度的线性拟合(实线)
Fig. 3. Measurements of radio frequency electric field (hollow dots) by EIT-AT spectra versus square root of signal generator output power, and its linear fit (solid line) with gradient of 3.929 (mV·cm-1)/mW1/2
在谐振区里德堡原子外差实验中,最佳本振场幅度选择为使得EIT峰刚刚开始分裂为两个可以分辨的AT峰时的信号强度[27]。在确定好本振信号的幅度及差频频率之后,逐步减小待测信号源输出功率,在示波器上可以看到正弦信号的峰峰值逐渐减小,在频谱仪上表现为差频信号谱线高度逐渐降低[17]。
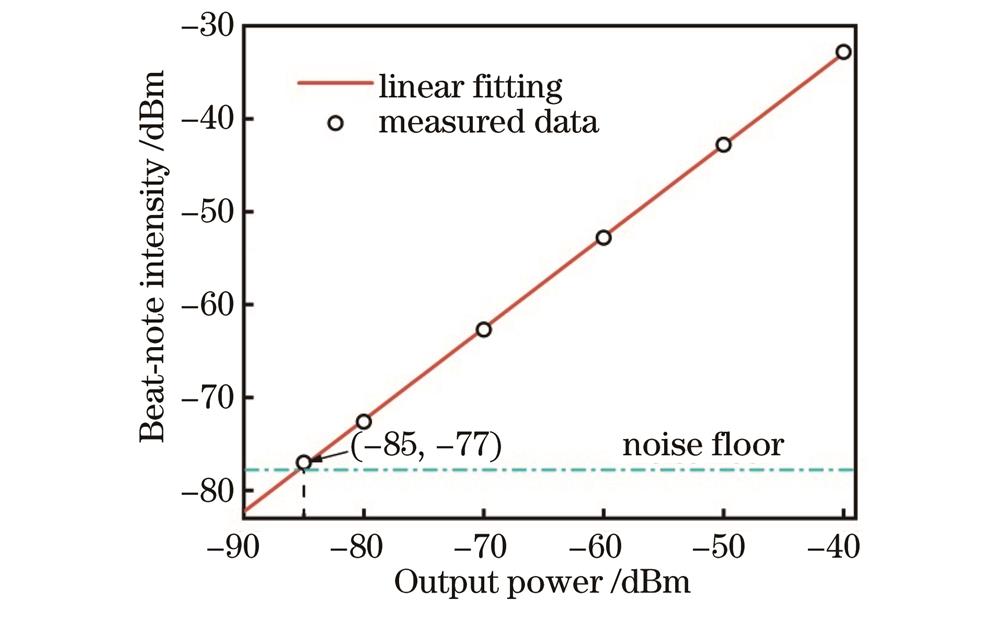
图 4. 差频信号强度随待测信号源输出功率的变化关系
Fig. 4. Beat-note intensity as a function of signal generator output power
4.2 非谐振区测量
非谐振区测量与谐振区类似,在获得最佳本振信号强度之后,保持频谱仪分辨率带宽不变,逐步减小待测信号源输出功率,直至差频信号谱线与频谱仪噪底持平。此时待测信号源的输出功率为
除了电场测量灵敏度之外,通过固定待测信号源输出功率至
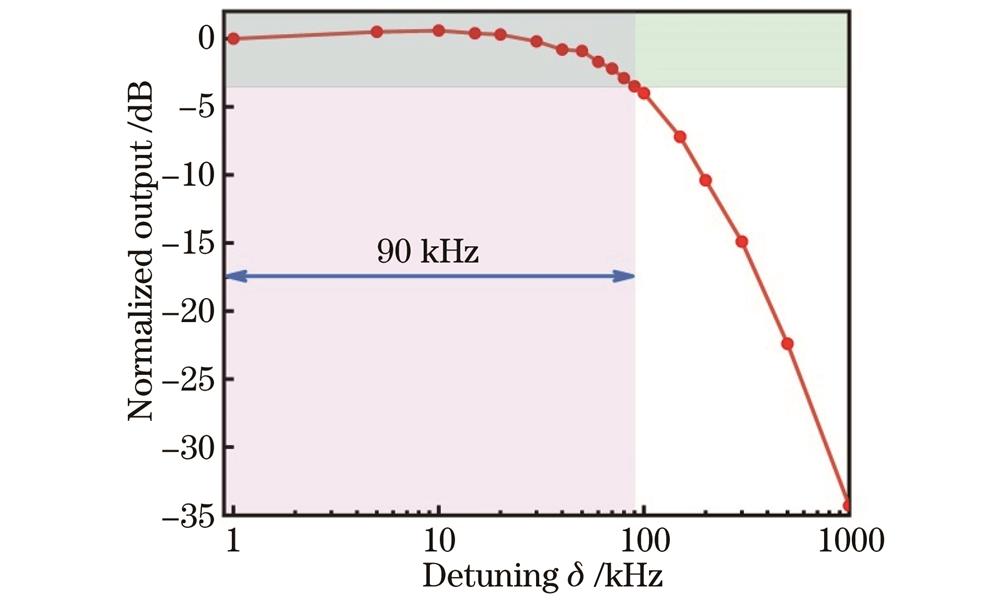
图 5. 归一化待测信号幅度随差频频率的变化曲线
Fig. 5. Variation curve of normalized signal amplitude under test with difference frequency
在非谐振区,原子气室的物理尺寸只有所探测射频信号波长的1/50,体现了里德堡原子在射频传感器小型化方面的巨大应用潜力。与谐振区相比,虽然非谐振区的电场测量灵敏度明显降低,但是在低频信号探测方面具有相对带宽及探测器小型化方面的优势。在实际应用中,需要根据所探测目标的频段及灵敏度要求,选用合适的里德堡原子作用区域进行探测。
5 结论
本文利用室温铯原子气室,选取谐振区和非谐振区两个典型频点,分别用喇叭天线及平行板波导作为微波发射装置,实验验证了里德堡原子的宽带高灵敏探测能力。利用里德堡原子外差技术,实现了谐振区2.63 GHz处最小场强为220.94 nV/cm和非谐振区300 MHz处最小场强为19 μV/cm的弱场探测,测量灵敏度分别达到
[1] 杨凯, 安强, 姚佳伟, 等. 基于Rydberg原子的100 kHz-40 GHz超宽带射频传感器[J]. 光学学报, 2022, 42(15): 1528002.
[2] Chu L J. Physical limitations of omni-directional antennas[J]. Journal of Applied Physics, 1948, 19(12): 1163-1175.
[4] Yang K, Mao R Q, An Q, et al. Amplitude-modulated RF field Rydberg atomic sensor based on homodyne technique[J]. Sensors and Actuators A: Physical, 2023, 351: 114167.
[5] Sedlacek J A, Schwettmann A, Kübler H, et al. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances[J]. Nature Physics, 2012, 8(11): 819-824.
[6] Prajapati N, Robinson A K, Berweger S, et al. Enhancement of electromagnetically induced transparency based Rydberg-atom electrometry through population repumping[J]. Applied Physics Letters, 2021, 119(21): 214001.
[7] Zhang L H, Liu Z K, Liu B, et al. Rydberg microwave frequency comb spectrometer[J]. Physical Review Applied, 2022, 18(1): 014033.
[8] Liu B, Zhang L H, Liu Z K, et al. Highly sensitive measurement of a megahertz rf electric field with a Rydberg-atom sensor[J]. Physical Review Applied, 2022, 18(1): 014045.
[9] Simons M T, Artusio-Glimpse A B, Holloway C L, et al. Continuous radio-frequency electric-field detection through adjacent Rydberg resonance tuning[J]. Physical Review A, 2021, 104(3): 032824.
[10] Jia F D, Liu X B, Mei J, et al. Span shift and extension of quantum microwave electrometry with Rydberg atoms dressed by an auxiliary microwave field[J]. Physical Review A: General Physics, 2021, 103(6): 63113.
[11] Yao J W, An Q, Zhou Y L, et al. Sensitivity enhancement of far-detuned RF field sensing based on Rydberg atoms dressed by a near-resonant RF field[J]. Optics Letters, 2022, 47(20): 5256-5259.
[12] Anderson D A, Paradis E G, Raithel G. A vapor-cell atomic sensor for radio-frequency field detection using a polarization-selective field enhancement resonator[J]. Applied Physics Letters, 2018, 113(7): 073501.
[13] Holloway C L, Prajapati N, Artusio-Glimpse A B, et al. Rydberg atom-based field sensing enhancement using a split-ring resonator[J]. Applied Physics Letters, 2022, 120(20): 204001.
[14] Simons M T, Haddab A H, Gordon J A, et al. Embedding a Rydberg atom-based sensor into an antenna for phase and amplitude detection of radio-frequency fields and modulated signals[J]. IEEE Access, 2019, 7: 164975-164985.
[15] Simons M T, Haddab A H, Gordon J A, et al. A Rydberg atom-based mixer: measuring the phase of a radio frequency wave[J]. Applied Physics Letters, 2019, 114(11): 114101.
[16] Jing M Y, Hu Y, Ma J, et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy[J]. Nature Physics, 2020, 16(9): 911-915.
[17] Cai M H, Xu Z S, You S H, et al. Sensitivity improvement and determination of Rydberg atom-based microwave sensor[J]. Photonics, 2022, 9(4): 250-263.
[18] 樊佳蓓, 郝丽萍, 白景旭, 等. 基于Rydberg原子的高灵敏微波探测与通信[J]. 物理学报, 2021, 70(6): 063201.
Fan J B, Hao L P, Bai J X, et al. High-sensitive microwave sensor and communication based on Rydberg atoms[J]. Acta Physica Sinica, 2021, 70(6): 063201.
[19] Holloway C L, Gordon J A, Jefferts S, et al. Broadband Rydberg atom-based electric-field probe for SI-traceable, self-calibrated measurements[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6169-6182.
[20] Meyer D H, Kunz P D, Cox K C. Waveguide-coupled Rydberg spectrum analyzer from 0 to 20 GHz[J]. Physical Review Applied, 2021, 15: 014053.
[21] Ryan C, Gonçalves L F, Sapiro R E, et al. Atomic 2D electric field imaging of a Yagi-Uda antenna near-field using a portable Rydberg-atom probe and measurement instrument[J]. Advanced Optical Technologies, 2019, 9(5): 305-312.
[22] 王延正, 付云起, 林沂, 等. 光学超表面集成原子气室仿真设计[J]. 激光与光电子学进展, 2022, 59(11): 1124001.
[23] 靳刚, 成永杰, 黄承祖, 等. 用于里德堡原子激发的激光系统实现[J]. 中国激光, 2022, 49(7): 0701003.
[25] 杜雷鸣, 谢彦召, 王绍飞. 平行板传输线特性阻抗仿真计算及解析修正[J]. 强激光与粒子束, 2015, 27(8): 083201.
[26] Holloway C L, Simons M T, Gordon J A, et al. Electric field metrology for SI traceability: systematic measurement uncertainties in electromagnetically induced transparency in atomic vapor[J]. Journal of Applied Physics, 2017, 121(23): 233106.
[27] Gordon J A, Simons M T, Haddab A H, et al. Weak electric-field detection with sub-1 Hz resolution at radio frequencies using a Rydberg atom-based mixer[J]. AIP Advances, 2019, 9(4): 045030.
[28] Anderson D A, Sapiro R E, Raithel G. A self-calibrated SI-traceable Rydberg atom-based radio frequency electric field probe and measurement instrument[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(9): 5931-5941.
[29] Mao R Q, Lin Y, Yang K, et al. A high-efficiency fiber-coupled Rydberg-atom integrated probe and its imaging applications[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(2): 352-356.
杨凯, 毛瑞棋, 孙占山, 李健兵, 付云起. 基于里德堡原子外差传感器的宽带高灵敏探测[J]. 光学学报, 2023, 43(17): 1728001. Kai Yang, Ruiqi Mao, Zhanshan Sun, Jianbing Li, Yunqi Fu. Broadband and Highly Sensitive Measurement Based on Rydberg Atomic Heterodyne Sensor[J]. Acta Optica Sinica, 2023, 43(17): 1728001.







