基于深度强化学习的量子奥托循环性能优化

李建松; 李海; 于文莉; 郝亚明

doi:doi:10.3969/j.issn.1007-5461.2025.01.007

量子电子学报, 2025, 42 (1): 70, 网络出版: 2025-03-13

基于深度强化学习的量子奥托循环性能优化【增强内容出版】

Performance optimization of quantum Otto cycle via deep reinforcement learning

论文大纲

李建松 ^1,*李海 ¹于文莉 ²郝亚明 ¹

作者单位

¹ 山东工商学院信息与电子工程学院, 山东烟台 264005

² 山东工商学院计算机科学与技术学院, 山东烟台 264005

AI高清视频导读

AI一图读本文 AI语音精读 AI语音超短摘要

注：本部分内容由 AI 自动生成，仅供您参考。对于您使用本站 AI 自动生成内容所产生的一切后果，本网站及平台运营方概不承担任何商业和法律责任，请您知悉。

摘要

针对通常情况下实现高性能的绝热捷径量子奥托循环 (QOC) 需要施加复杂调控场的难题, 研究了实验上相对便于操控的线性驱动场下QOC的性能特征。利用基于策略函数的深度强化学习, 对以单量子比特为工质的QOC膨胀与压缩过程的附加驱动场进行优化, 实现了线性驱动场下高性能的QOC。与非绝热自由演化方案下的QOC对比, 优化附加驱动方案下的QOC在输出功、功率以及效率方面都表现出显著的优越性。特别是在较短循环周期中, 自由演化方案下的QOC因大量不可逆功的产生, 完全抑制了正功的输出, 然而优化驱动方案下的QOC却仍能正常运行(有正功输出)。本工作初步检验了深度强化学习在优化量子热机性能中的有效性。

Abstract

In response to the challenge that complicated control fields are generally required for realizing the high-performance shortcuts to adiabaticity quantum Otto cycle (QOC), the performance characteristics of QOC under linear driving field which is easy to manipulate in experiment, are studied in this work. Using the strategy-based deep reinforcement learning, the driving field added during the expansion and compression processes of QOC with single qubit as the working medium is optimized, and then the high-performance QOC under linear driving field can be realized. Compared with the scheme of QOC with the non-adiabatic free evolution, the QOC under the optimized additional driving scheme exhibits significant advantages in the output work, power and efficiency. Especially, in the case of short-cycle period, for the QOC under free evolution scheme, the output of positive work is completely suppressed due to the generation of a large amount of irreversible work, while the QOC under the optimized driving scheme can still operate normally (with output positive work). This work preliminarily tests the validity of deep reinforcement learning in optimizing the performance of quantum engine.

0　引言

能量转化是研究物质热力学性质的主要切入点之一。随着纳米技术的发展, 微观量子系统下热能的高效利用逐渐受到人们的关注, 推动了量子热机的理论和实验研究。量子热机是研究微观系统下能量转换与控制的重要平台, 能够促进人们对微观量子系统下能量转换物理机制的深入认识。这对纳米器件、分子马达以及超大规模集成电路领域的能量传输、转换控制等方面具有实际应用价值。

量子奥托循环(QOC)是热机循环的一种重要循环方式。与经典奥托循环类似, 一个理想的QOC包括两个等容热化过程和两个准静态绝热做功过程。在理想的QOC中, 准静态绝热膨胀/压缩过程在保证量子奥托热机获得最高效率的同时, 也会导致其平均输出功率趋于零。因此, 研究如何获得较高QOC效率的同时又提升其输出功率是必要的。近年来, 学者们提出了一种加速系统绝热演化的方法—绝热捷径(STA) 技术^[1-5], 其中反向透热补偿驱动法^[6-10]是较常见的一种, 被应用于一维谐振子系统^[6,7]、单/双比特^[8]和多体自旋链系统^[9,10]等构造的QOC。在理论上, STA技术已被证明对QOC性能的提升是有效的。但是, 绝热捷径方案下的控制场函数通常为高阶非线性的复杂函数, 在实验上不便于操控。近年来, 机器学习作为数据处理与计算的强大工具, 已被广泛应用于统计、控制等多学科。近期, 机器学习也开始被应用于量子物理领域, 执行某些特定的任务, 如量子态制备^[11,12]、非平衡量子系统动力学演化路径调控^[13]以及量子热机性能优化^[14,15]等。然而, 机器学习算法在量子热机中的应用研究目前尚处于初步探索阶段, 相关的研究成果较少。基于不同特征的量子热机模型如何借助机器学习实现性能优化是值得探索的课题。

本文以单自旋量子比特系统为工质, 研究了热机在便于调控的线性驱动场下执行膨胀/压缩过程的有限时间内的QOC的性能。结合基于策略函数的深度强化学习算法, 分析了QOC膨胀和压缩过程中附加驱动场的最优驱动策略(附加驱动场强度的优化分布), 探讨了优化附加驱动方案下QOC的性能特征。

1　QOC模型

本研究以单量子比特系统为工质, 研究其在磁场调控下执行QOC的热力学性能。考虑工质满足 Landau-Zener模型, 则其哈密顿量可表示为

$H_{0} (t) = b_{x} (t) σ_{x} + b_{z} (t) σ_{z}$ ,(1)

式中 $b_{x} (t)$ 与 $b_{z} (t)$ 分别代表沿 $x$ 和 $z$ 轴添加的外磁场。类似于STA方案下的驱动方式, 在系统膨胀/压缩过程中施加沿 $y$ 轴方向的附加驱动场, 记为 $H_{e d} (t) = - f_{e d} (t) σ_{y}$ , $f_{e d} (t)$ 代表含时驱动场强度。因此, 在膨胀/压缩演化过程中, 系统的总哈密顿量可表示为

$H (t) = b_{x} (t) σ_{x} + b_{z} (t) σ_{z} - f_{e d} (t) σ_{y}$ .(2)

为了简化研究, 设定 $x$ 轴方向的磁场强度固定不变, $b_{x} (t) = B_{x}$ 。对于反向透热补偿方案下的QOC, 通常要求沿 $z$ 轴方向施加的磁场 $b_{z} (t)$ 为复杂的高阶时间函数, 这在实际实验中较难调控。因此, 本文考虑热机在膨胀/压缩过程中施加较易控制的线性磁场, 即膨胀/压缩过程分别有 $b_{z}^{e x p} (t) = B_{z} (τ - t) / τ$ 和 $b_{z}^{c o m p} (t) = B_{z} t / τ$ , $t \in [0, τ]$ , $B_{z}$ 和 $τ$ 分别代表热机膨胀前磁场强度和膨胀或压缩过程时长。此时, 热机膨胀与压缩过程中的哈密顿量可表示为

$H_{}^{j} (t) = H_{0}^{j} (t) - f_{e d}^{j} (t) σ_{y} = B_{x} σ_{x} + b_{z}^{j} (t) σ_{z} - f_{e d}^{j} (t) σ_{y}$ ,(3)

式中: $H_{0}^{j} (t)$ 、 $H_{}^{j} (t)$ 分别代表工质在膨胀 ( $j = e x p$ ) 和压缩过程 ( $j = c o m p$ ) 中自由演化 [ $无附加场作用, f_{e d}^{j} (t) = 0]$ 和施加附加驱动场 [ $f_{e d}^{j} (t) \neq 0$ ] 情况下的哈密顿量, 其中 $H_{0}^{j} (t) = B_{x} σ_{x} + b_{z}^{j} (t) σ_{z}$ 。

1.1　理想绝热QOC

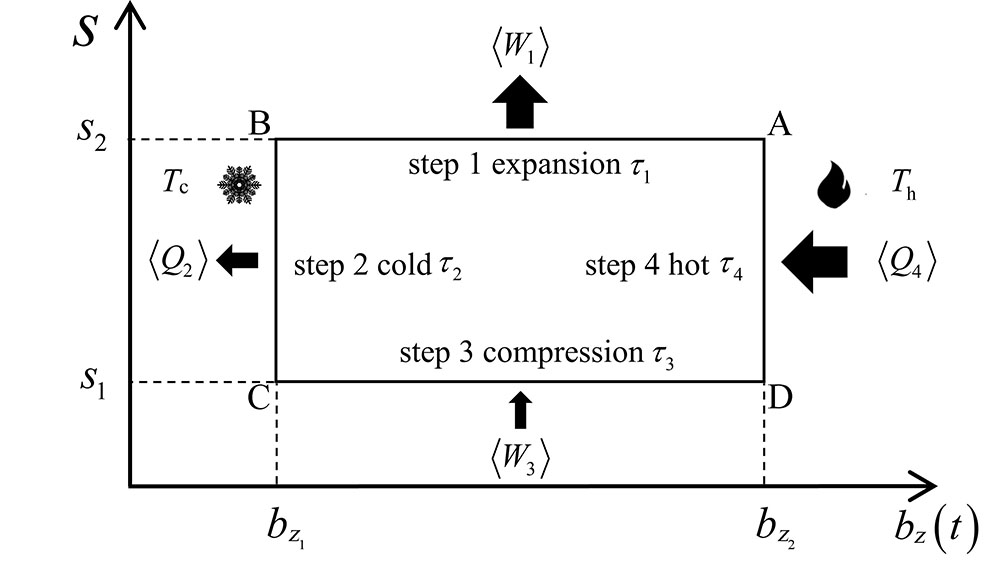
在不考虑施加附加驱动场的理想QOC中, 整个循环由两个量子绝热过程和两个等容热化过程构成(如图1所示), 具体执行过程如下:

图 1. 理想的量子奥托循环示意图

Fig. 1. Diagram of the ideal QOC

下载图片查看所有图片

第一步: 绝热膨胀过程(A→B)。工质与温度为 $T_{h}$ 的高温库脱离, 并执行 $τ_{1}$ 时长的等熵( $s_{2}$ )膨胀。这个过程中含时控制参数 $b_{z} (t)$ 非常缓慢地由 $b_{z_{2}}$ 减小至 $b_{z_{1}}$ (满足准静态过程)。该过程中系统完全孤立于环境, 因此无热交换发生, 系统仅仅对外做功, 做功量为

$〈W_{1}〉 = {〈H_{0}^{e x p} (b_{z_{2}})〉}_{ρ_{A}} - {〈H_{0}^{e x p} (b_{z_{1}})〉}_{ρ_{B}} = \sum_{i = 1}^{2} P_{i}^{A} (E_{i}^{A} - E_{i}^{B})$ ,(4)

式中: $ρ_{A, B} = \sum_{i = 1}^{2} P_{i}^{A, B} |E_{i}^{A, B}〉〈E_{i}^{A, B}|$ , 代表工质处于A和B点处的密度矩阵, 其中 $E_{i}^{A, B}$ $(|E_{i}^{A, B}〉)$ ( $i = 1,2$ ) 为工质于A和B处对应的哈密顿量 $H_{0}^{e x p} (b_{z_{2}})$ 和 $H_{0}^{e x p} (b_{z_{1}})$ 的能量本征值, 且 $E_{1}^{A} = - \sqrt[]{B_{x}^{2} + b_{z_{2}}^{2}}$ 、 $E_{2}^{A} = \sqrt[]{B_{x}^{2} + b_{z_{2}}^{2}}$ 、 $E_{1}^{B} = - \sqrt[]{B_{x}^{2} + b_{z_{1}}^{2}}$ 、 $E_{2}^{B} = \sqrt[]{B_{x}^{2} + b_{z_{1}}^{2}}$ ; $P_{i}^{A, B}$ 表示工质处于相应能级上的概率, 且满足 $P_{i}^{B} = P_{i}^{A} = 〈E_{i}^{A}| e^{- β_{h} H_{0}^{e x p} (b_{z_{2}})} / Z_{A} |E_{i}^{A}〉$ (准静态过程系统无能级跃迁发生), $Z_{A} = T r [e^{- β_{h} H_{0}^{e x p} (b_{z_{2}})}] = \sum_{i = 1}^{2} e^{- β_{h} E_{i}^{A}}$ 为配分函数。

第二步: 等容冷却过程 (B→C)。在该过程中保持控制参数 $b_{z_{1}}$ 不变。工质与温度为 $T_{c}$ 的冷库持续接触时长 $τ_{2}$ 后达到热平衡, 同时工质的熵由 $s_{2}$ 减小至 $s_{1}$ 。在该过程中工质能级不发生改变(工质不对外界做功), 工质与冷库间发生的热交换量可表示为

$〈Q_{2}〉 = T r [(ρ_{B} - ρ_{C}) H_{0}^{e x p} (b_{z_{1}})] = \sum_{i = 1}^{2} (P_{i}^{B} - P_{i}^{C}) E_{i}^{B}$ ,(5)

式中: $ρ_{C} = \sum_{i = 1}^{2} P_{i}^{C} |E_{i}^{C}〉〈E_{i}^{C}|$ 为热态, $P_{i}^{C} = 〈E_{i}^{C}| e^{- β_{c} H_{0}^{e x p} (b_{z_{1}})} / Z_{C} |E_{i}^{C}〉 = e^{- β_{c} E_{i}^{C}} / Z_{C}$ (式中 $β_{c} = 1 / T_{c}$ )代表工质处于第 $i$ 个本征能级 $E_{i}^{C}$ ( $i = 1,2$ )的布居。

第三步: 绝热压缩过程 (C→D)。工质与温度为 $T_{c}$ 的低温库脱离, 并执行时长为 $τ_{3}$ 的等熵 ( $s_{1}$ ) 压缩过程。此过程为第一步的逆过程, 工质控制参数非常缓慢地由 $b_{z_{1}}$ 返回至初始值 $b_{z_{2}}$ 。此演化过程中系统不发生能级跃迁, 即工质末态 $ρ_{D}$ 与初态 $ρ_{C}$ 有相同的布居。此过程中系统无热耗散, 系统对外做功量为

$〈W_{3}〉 = {〈H_{0}^{c o m p} (b_{z_{1}})〉}_{ρ_{C}} - {〈H_{0}^{c o m p} (b_{z_{2}})〉}_{ρ_{D}} = \sum_{i = 1}^{2} P_{i}^{C} (E_{i}^{C} - E_{i}^{D})$ ,(6)

式中 $ρ_{D} = \sum_{i = 1}^{2} P_{i}^{D} |E_{i}^{D}〉〈E_{i}^{D}| = P_{i}^{C} |E_{i}^{D}〉〈E_{i}^{D}|$ , $E_{i}^{D}$ $(|E_{i}^{D}〉)$ 为工质在D处哈密顿量 $H_{0}^{c o m p} (b_{z_{2}})$ 的能量本征值(本征态)。

第四步: 等容加热过程 (D→A)。此过程与第二步中的热交换过程类似, 工质在保持能级不变的情形下与温度为 $T_{h}$ 的高温库接触。经过时间 $τ_{4}$ 后, 工质的熵由 $s_{1}$ 返回至初始态下的 $s_{2}$ , 即系统返回初始态, 循环结束。在此过程中工质不对外做功, 其从高温库吸收的热量为

$〈Q_{4}〉 = T r [(ρ_{A} - ρ_{D}) H_{0}^{e x p} (b_{z_{1}})] = \sum_{i = 1}^{2} (P_{i}^{A} - P_{i}^{D}) E_{i}^{A}$ .(7)

考虑到绝热膨胀与压缩过程互为逆过程, 其哈密顿量满足 $H_{0}^{c o m p} (b_{z} (t)) = H_{0}^{e x p} (b_{z} (t))$ , 则能量本征值也对应相等, 即 $E_{i}^{C} = E_{i}^{B}$ 和 $E_{i}^{D} = E_{i}^{A}$ ( $i = 1,2$ )。因此, 对于单个理想绝热QOC, 工质能输出的总功可表示为

$W_{a d}^{t o t} = 〈W_{1}〉 + 〈W_{3}〉 = \sum_{i = 1}^{2} (P_{i}^{A} - P_{i}^{C}) (E_{i}^{A} -$ $E_{i}^{B}$ ) .(8)

QOC的平均输出功率和效率可分别表示为

$P_{a d} = \frac{W_{a d}^{t o t}}{τ_{c y c l e}} = \frac{〈W_{1}〉 + 〈W_{3}〉}{τ_{c y c l e}} = \frac{\sum_{i = 1}^{2} (P_{i}^{A} - P_{i}^{C}) (E_{i}^{A} - E_{i}^{B})}{τ_{c y c l e}}$ ,(9)

和

$η_{a d} = \frac{W_{a d}^{t o t}}{〈Q_{4}〉} = \frac{〈W_{1}〉 + 〈W_{3}〉}{〈Q_{4}〉} = \frac{\sum_{i = 1}^{2} (P_{i}^{A} - P_{i}^{C}) (E_{i}^{A} - E_{i}^{B})}{\sum_{i = 1}^{2} (P_{i}^{A} - P_{i}^{D}) E_{i}^{A}}$ .(10)

另外, QOC绝热膨胀与压缩过程经历的时长 $τ_{1,3}$ 通常远大于工质与高、低温库接触实现工质热化的时长 $τ_{2,4}$ , 即 $τ_{1,3} ≫ τ_{2,4}$ 。因此, 单个QOC的时长可表示为: $τ_{c y c l e} = τ_{1} + τ_{2} + τ_{3} + τ_{4} \approx τ_{1} + τ_{3}$ 。为方便, 考虑膨胀与压缩过程时间相同, 即 $τ_{1} = τ_{3} = τ$ , 则循环周期为 $τ_{c y c l e} = 2 τ$ 。对于理想绝热QOC, 膨胀与压缩过程为准静态过程 ( $τ \to \infty$ ), 所以其平均输出功率趋于零, 即 $P_{a d} = \underset{τ \to \infty}{l i m} W_{a d}^{t o t} / 2 τ = 0$ 。

1.2　非理想绝热QOC

为实现非零的高功率热循环, 重点研究了(2) 式描述的附加驱动场的循环方案和无附加驱动场的自由演化方案。对于附加驱动方案下的QOC, 附加场的添加必然会导致外界驱动系统在热机输出功的过程中存在额外能量的消耗。通常, 这部分能量消耗也被称为能量成本。在膨胀/压缩过程中外界 (附加场) 的能量成本可表示为^[13]

$〈C_{j}〉 = \frac{1}{τ} \int_{0}^{τ} T r \{ρ_{j} (t) [H^{j} (t) - H_{0}^{j} (t)]\} d t$ ,(11)

式中 $ρ_{j} (t)$ 、 $〈C_{j}〉$ 分别代表系统在膨胀过程 ( $j = e x p$ ) 和压缩过程 ( $j = c o m p$ ) 中工质演化的密度矩阵和附加驱动场的能量成本。单个QOC中附加驱动场的总能量成本为 $〈C_{t o t}〉 = 〈C_{e x p}〉 + 〈C_{c o m p}〉$ 。与理想绝热方案相比, 自由演化循环方案下工质在有限时间内的膨胀/压缩过程将伴随不可逆功(热耗散)的产生, 并导致输出功的减少。通常, 不可逆功定义为^[10]

$〈W_{i r r}〉 = \frac{1}{β} S (ρ_{t} | | ρ_{t}^{a d})$ ,(12)

式中 $S (ρ_{t} | | ρ_{t}^{a d}) = T r (ρ_{t} l n ρ_{t} - ρ_{t} l n ρ_{t}^{a d})$ , 表示工质自由演化态 $ρ_{t}$ 相对于理想绝热态 $ρ_{t}^{a d}$ 的相对熵。工质在一般循环方案(包括自由演化和附加驱动方案)下对外所做的功通常表示为^[16]

$〈{W_{j}}^{s}〉 = - \int_{0}^{τ} ρ_{j}^{s} (t) {\dot{H}}_{0}^{j} (t) d t$ ,(13)

式中 $〈{W_{j}}^{s}〉$ 代表系统附加驱动方案 ( $s = e d$ ) 和自由演化方案 ( $s = f r e e$ ) 下在膨胀过程 ( $j = e x p$ ) 和压缩过程 ( $j = c o m p$ ) 中对外所做的功。这里, $〈{W_{j}}^{s}〉 > 0$ 和 $〈{W_{j}}^{s}〉 < 0$ 分别对应系统在膨胀或压缩过程中对外做正功和负功。这里需要指出的是: 在附加驱动或自由演化循环方案下, 系统在膨胀和压缩过程中一般很难达到完全的绝热演化, 且在不同的循环方案下, 工质与高、低温库接触后发生的热交换量通常都不相同。为便于区别不同循环方案下的热交换量, 记 ${\tilde{Q}}_{m}^{s}$ ( $m = c, h$ )为工质在附加驱动方案 ( $s = e d$ ) 和自由演化方案 ( $s = f r e e$ )下与低温库( $m = c$ ) 和高温库( $m = h$ )接触执行热化过程的热交换量。这里, ${\tilde{Q}}_{m}^{s} > 0$ ( ${\tilde{Q}}_{m}^{s} < 0$ )表示工质放热(吸热)量。因此, 附加驱动循环方案下QOC的净输出功为

$W_{e d}^{t o t} = 〈W_{e x p}^{e d}〉 + 〈W_{c o m p}^{e d}〉 - 〈C_{t o t}〉$ ,(14)

相应的平均输出功率和效率可分别表示为

$P_{e d} = \frac{W_{e d}^{t o t}}{τ_{c y c l e}} = \frac{〈W_{e x p}^{e d}〉 + 〈W_{c o m p}^{e d}〉 - 〈C_{t o t}〉}{τ_{c y c l e}}$ ,(15)

$η_{e d} = \frac{〈W_{e x p}^{e d}〉 + 〈W_{c o m p}^{e d}〉}{{\tilde{Q}}_{h}^{e d}_{} + 〈C_{t o t}〉}$ .(16)

类似地, 在自由演化方案下, QOC的净输出功为

$W_{f r e e}^{t o t} = 〈W_{e x p}^{f r e e}〉 + 〈W_{c o m p}^{f r e e}〉$ ,(17)

平均输出功率和效率为

$P_{f r e e} = \frac{W_{f r e e}^{t o t}}{τ_{c y c l e}} = \frac{〈W_{e x p}^{f r e e}〉 + 〈W_{c o m p}^{f r e e}〉}{τ_{c y c l e}}$ ,(18)

$η_{f r e e} = \frac{〈W_{e x p}^{f r e e}〉 + 〈W_{c o m p}^{f r e e}〉}{{\tilde{Q}}_{h}^{f r e e}_{}}$ .(19)

另外, 值得说明的是, 关于自由演化方案下QOC的不可逆功 $〈W_{i r r}〉$ 的定义, 除了可以表示为 (12) 式中相对熵形式外, 有时也被表示为理想绝热功与自由演化功的差的形式^[17], 即 $〈W_{i r r}〉 = W_{a d}^{t o t} - W_{f r e e}^{t o t}$ 。但是, 这两种不同形式的定义都能有效刻画自由演化方案下QOC产生的不可逆功与净输出功之间的竞争关系。因此, 本文将在后文中仅选择 (12) 式的定义形式对不可逆功进行分析。

2　基于深度强化学习的附加驱动场优化策略

施加附加驱动场对QOC性能的影响程度与外界驱动场强度随时间分布 (或驱动场强度序列) 密切相关。这里, 考虑通过引入基于策略函数的深度强化学习来寻找最优驱动场的分布特征, 从而获得最优驱动循环方案。

强化学习的本质是智能体与环境进行交互, 得到环境的反馈奖励, 然后使用从环境中获得的长期累计回报奖励来指导智能体改善行为, 找到可以使环境奖励最大化的策略。使用策略函数 $g_{θ} (a_{k} |s_{k})$ 表示在给定环境状态 $s_{k}$ 的情况下, 智能体选择动作 $a_{k}$ 的概率, $θ$ 代表神经网络的参数。对于连续动作空间, 选择策略函数为高斯函数^[18], 可表示为

$g_{θ} (a_{k} = a | s_{k} = s) = e x p [- \frac{{[a - μ_{θ} (s)]}^{2}}{2 σ^{2}}] / (\sqrt[]{2 π} σ)$ ,(20)

式中 $σ$ 和 $μ$ 分别用指定参数和神经网络表示。

将工质在图1中的A和C点处的密度矩阵作为初始输入态, 将绝热膨胀/压缩演化时长划分成一定数量等长的时间间隔 ( $δ τ = τ / N$ , $δ τ$ 代表时间间隔, $τ$ 为膨胀/压缩过程演化时长)。在第 $k$ 个间隔, $t \in [t_{k - 1}, t_{k}]$ ( $t_{k} = k δ τ$ ), 通过神经网络预测 $μ_{θ} (s_{k - 1})$ , $s_{k - 1}$ 代表工质工作于 $t_{k - 1}$ 时所处的状态 (或能级布居), 根据 (20) 式的策略函数, 得到 $t_{k}$ 时智能体随机动作 $a_{k}$ , 即 $t_{k}$ 时的附加驱动场强度为 $f_{e d} (t_{k}) = a_{k}$ , 且此强度一直持续到 $t_{k + 1}$ 时进行更新。附加驱动场优化的算法流程如图2所示。

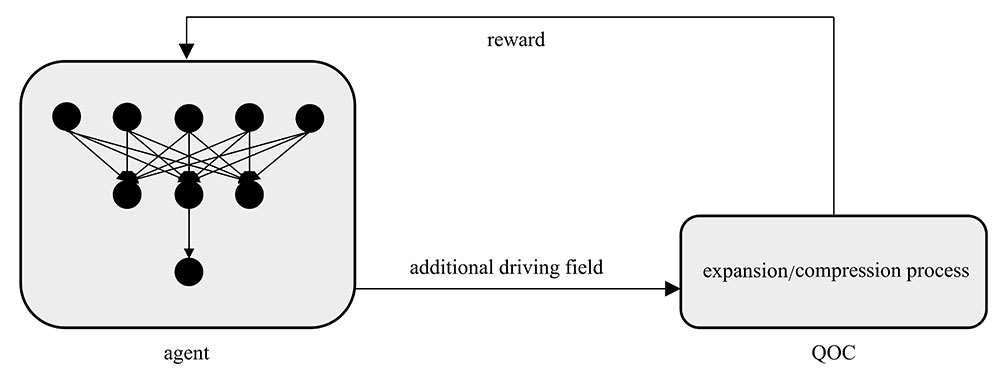
图 2. 强化学习优化附加驱动场示意图

Fig. 2. Diagram of optimization of the additional driving field by reinforcement learning

下载图片查看所有图片

首先, 给agent的网络输入端输入QOC膨胀/压缩时的初始热态, 神经网络基于策略的深度学习算法, 预测工质在接下来 $δ τ$ 演化时长内的附加驱动场强度; 然后, 热机工质在网络预测的附加驱动场下执行膨胀/压缩演化, 且将工质演化 $δ τ$ 时长后的态作为agent网络新的输入态, 执行新的附加驱动强度预测。其中, 在每完成一个完整回合后, 给智能体一个奖励值 $R$ , 并使用梯度上升算法把网络参数 $θ$ 更新为

$θ = θ + α R \sum_{a_{k}} \nabla_{θ} l o g g_{θ} (a_{k}, s_{k})$ ,(21)

式中 $α$ 是学习率。

在选择 $g_{θ} (a_{k} |s_{k})$ 的基础上, 采用随机梯度下降法和批量数据对神经网络进行训练, 所用成本函数满足 (21)式的条件, 其可表示为^[13]

$C = (1 / 2 σ^{2}) {\sum_{a_{k}} R | a_{k} - μ_{θ} (s_{k}) |}^{2}$ .(22)

利用以上算法, 分别对QOC的膨胀和压缩过程的附加驱动场强度分布进行优化。在算法中, 分别设置 $R = 100 〈W_{1}〉$ 和 $R = 100 (1 - |〈W_{3}〉|)$ 为QOC膨胀和压缩过程的奖励值。此外, 设置神经网络的输出值 $|μ_{θ} (s_{i})| < M$ , $M$ 为设置驱动场强度的最大值, 通过改变 $M$ 来控制附加驱动场的能量成本。通过限制 $M$ 的大小, 即可控制附加驱动场强度的大小, 实现对QOC输出功的优化。在每轮神经网络训练中, 初始输入相同的系统态信息, 与环境交互产生的经验数据作为训练数据, 并利用这些经验数据对策略函数 $g_{θ} (a_{k} |s_{k})$ 进行更新。训练完成后, 得到优化的附加驱动场 $f_{e d} (t)$ , 即最优的附加驱动场强度序列(分布)。

本文搭建的神经网络由 $u n i t s = 50$ 的长短期记忆神经元、具有30个神经元的全连接层和单个神经元输出层组成。激活函数为tanh函数, 采用Adam优化器进行网络训练。在训练过程中, 取batch=30,

epoch=100, 高斯函数参数 $σ = 0.1$ , 驱动场强度最大值取 $M = 0.1$ 。

3　数值分析与讨论

接下来, 通过数值模拟对附加驱动方案和自由演化方案下QOC的性能特征进行分析。为方便研究, 固定热机在膨胀/压缩过程中 $x$ 轴方向的磁场强度 $B_{x} = 0.1$ , 并设 $z$ 轴方向的磁场强度在膨胀/压缩过程初、末值满足 $b_{z}^{e x p} (0) = b_{z}^{c o m p} (τ) = B_{z} = 0.5$ 和 $b_{z}^{e x p} (τ) = b_{z}^{c o m p} (0) = 0$ 。高、低温库的温度参数取 $T_{h} = 10$ 和 $T_{c} = 1$ 。

3.1　能量成本和输出功

基于本文考虑的热机模型, 通过施加附加驱动场, 可以有效抑制QOC过程中不可逆功的产生, 从而提高热机功的输出。但是, 附加驱动场的添加通常会产生一定能量的消耗或能量成本。

图3对比了优化的附加驱动与自由演化两种方案下QOC过程中的能量消耗 [图3(a)] 和输出功 [图3(b) $P_{e d}^{m a x}$ ]。从图3(a)可以看出: QOC演化周期越长 ( $τ$ 越大), 热机执行速度 (膨胀/压缩速度) 则越慢, 两种方案下的能量消耗 $〈C_{t o t}〉$ (附加驱动场能量成本) 和 $〈W_{i r r}〉$ (自由演化不可逆功) 越小, 但是在相同循环周期 $τ_{c y c l e}$ ( $τ_{c y c l e} = 2 τ$ ) 下, 自由演化方案中因“量子摩擦”引起的不可逆功 $〈W_{i r r}〉$ 总是大于优化驱动方案中的能量成本消耗 $〈C_{t o t}〉$ , 即 $〈W_{i r r}〉 > 〈C_{t o t}〉$ , 且循环执行速度越快 ( $τ$ 越小), 不可逆功 $〈W_{i r r}〉$ 的增量比能量成本消耗 $〈C_{t o t}〉$ 的增量越显著。这也导致在较短的循环周期中 ( $τ$ 在较小的取值区间), 自由演化方案下较大的不可逆功的产生完全抑制了循环QOC正功的输出。如图3(b)所示, 当 $6 \leq τ \leq 8$ 时, 自由方案下QOC无正功输出, 即 $W_{f r e e}^{t o t} \leq 0$ (QOC不能正常运作), 而优化附加驱动方案下则仍能输出正功, 即 $W_{e d}^{t o t} > 0$ 。同时, 随着循环周期的增加, 优化驱动方案下QOC的输出功较自由演化方案能够更快地逼近理想绝热QOC下热机的输出功 $W_{a d}^{t o t}$ 。这里需要指出的是: 在图3(b)中 $W_{a d}^{t o t}$ 代表热机执行准静态膨胀/压缩 (循环时间无穷长, 即 $τ \to \infty$ ) 的理想绝热QOC的输出功, 并非代表有限循环时间 $τ$ 内热机输出恒定不变的功, 即热机的输出功与循环时间无关。另外, 在图3(b)中添加 $W_{a d}^{t o t}$ 的主要目的是为了较清楚地展示自由演化和优化附加驱动两种循环方案下QOC输出功 $W_{f r e e}^{t o t}$ 和 $W_{e d}^{t o t}$ 随循环时间的增加, 逐渐逼近理想绝热功 $W_{a d}^{t o t}$ 的程度。

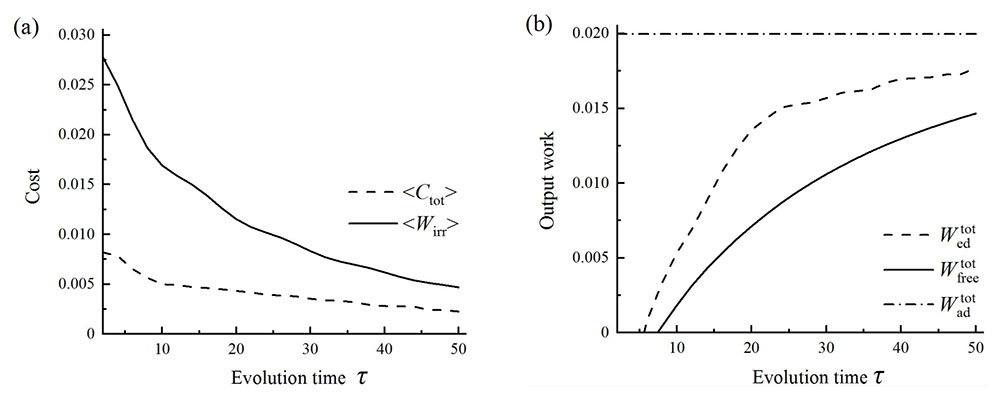
图 3. 优化附加驱动方案与自由演化方案下的能量消耗与输出功对比。(a) 能量成本 $〈C_{t o t}〉$ 与不可逆功 $〈W_{i r r}〉$ ; (b) 输出功 $W_{e d}^{t o t}$ 和 $W_{f r e e}^{t o t}$

Fig. 3. Comparison of energy cost and output work in the optimization additional driving and free evolution schemes.(a) Energy cost $〈C_{t o t}〉$ and irreversible work $〈W_{i r r}〉$ ; (b) Output work $W_{e d}^{t o t}$ and $W_{f r e e}^{t o t}$

下载图片查看所有图片

3.2　QOC的效率和功率

除输出功之外, 功率和效率也是反映热机性能的另外两个核心指标。下面将对优化附加驱动和自由演化两种方案下QOC的功率和效率进行对比分析, 对比情况如图4所示。

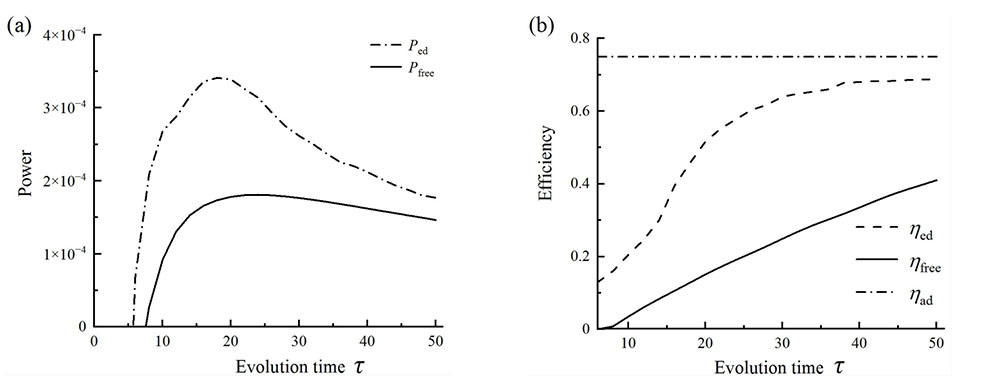
图 4. 优化附加驱动方案与自由演化方案下QOC性能的对比。(a) 功率 $P_{e d}$ 和 $P_{f r e e}$ ; (b) 效率 $η_{e d}$ 和 $η_{f r e e}$

Fig. 4. Comparison of performance of QOC of the optimization additional driving and free evolution schemes.(a) Power $P_{e d}$ and $P_{f r e e}$ ; (b) Efficiency $η_{e d}$ and $η_{f r e e}$

下载图片查看所有图片

从图4(a) 可以看出: 在输出功率方面, 优化附加驱动方案和自由演化方案下的功率 $P_{e d}$ 和 $P_{f r e e}$ 均随循环时间参数τ的增加先增加后减小; 由于在相同循环时间下优化附加驱动方案QOC的输出功总大于自由演化的, 即 $W_{e d}^{t o t} > W_{f r e e}^{t o t}$ [见图3(b)], 因此, 优化附加驱动方案QOC也表现出较大的输出功率, 即 $P_{e d} > P_{f r e e}$ 。此外, 也注意到: 优化附加驱动方案下QOC能够在较短循环周期中获得最大功率, 即前者最大输出功率 $P_{e d}^{m a x} = 3.4 \times 10^{- 4}$ 对应 $τ = 18$ , 后者最大功率 $P_{f r e e}^{m a x} = 1.8 \times 10^{- 4}$ 对应 $τ = 24$ , 且两类循环方案的最大功率比接近1.9, 即 $P_{e d}^{m a x} / P_{f r e e}^{m a x} \approx 1.9$ 。由图4(b)可以看出: 在效率方面, 优化附加驱动方案也展示出明显优势, 即有 $η_{e d} > η_{f r e e}$ 。同时, 优化附加驱动QOC效率 $η_{e d}$ 能够较快地接近理想绝热循环下的效率 $η_{a d} \approx 0.75$ 。此外, 在优化附加驱动QOC的最大功率下 ( $τ = 18$ 处), 其效率可达到 $η_{e d} = 0.448$ , 而相同循环周期下自由演化QOC的效率则为 $η_{f r e e} = 0.129$ , 此处两循环方案下的效率比接近3.5, 即 $η_{e d} / η_{f r e e} \approx 3.5$ 。图5给出了QOC存在最大输出功率 $P_{e d}^{m a x}$ (循环参数 $τ = 18$ )下, 热机在膨胀 [图5(a)] 和压缩过程 [图5(b)] 中的最优附加驱动场 $f_{e d}^{e x p}$ 和 $f_{e d}^{c o m p}$ 的分布。从 [图5(a)] 和 [图5(b)] 可以看出: 热机在膨胀过程与压缩过程中的最优驱动场序列既有正向驱动脉冲 ( $f_{e d}^{e x p, c o m p} > 0$ ), 又有反向驱动脉冲 ( $f_{e d}^{e x p, c o m p} < 0$ )。但是, 与膨胀过程相比, 整个压缩过程包含较少的负向驱动脉冲 (仅在0.6 $τ$ 至0.7 $τ$ 期间出现)。

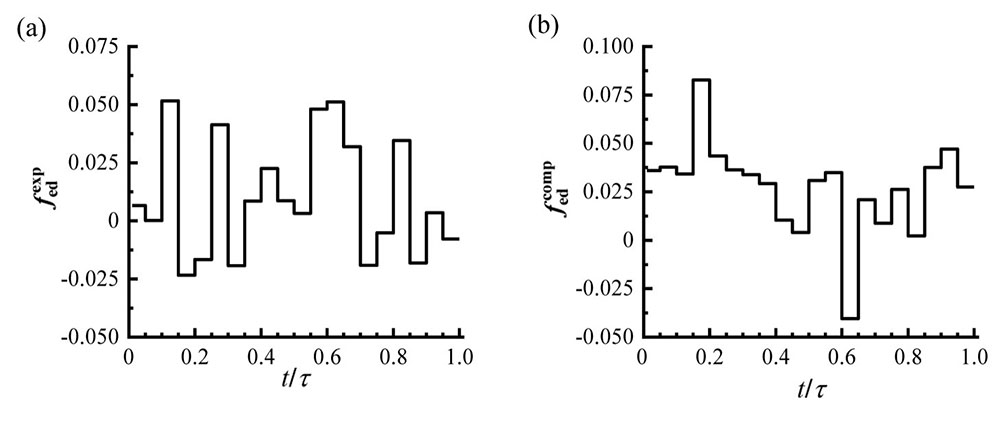
图 5. 在 $τ = 18$ 情况下, 优化附加驱动场强度的分布特征。(a) 膨胀过程的驱动场 $f_{e d}^{e x p}$ 分布; (b) 压缩过程的驱动场 $f_{e d}^{c o m p}$ 分布

Fig. 5. Optimization distribution of additional driving field with $τ = 18$ . (a) $f_{e d}^{e x p}$ in expansion process; (b) $f_{e d}^{c o m p}$ in compression process

下载图片查看所有图片

4　结论

本文以单量子比特系统为工质, 构造了基于策略函数的深度强化学习优化方案下的有限时间内的QOC。对比分析了热机在线性驱动场中执行自由演化和机器学习优化附加驱动场演化下的热机性能。结果表明: 利用深度强化学习优化QOC膨胀和压缩过程的附加驱动场, 其整体性能明显优于自由演化方案下的情形。特别地, 优化附加驱动方案下的QOC在较短循环周期下仍可有效运行, 而自由演化方案则失效 (无正功输出)。此外, 优化附加驱动方案下的QOC的最大功率和效率也均显著优于自由演化方案下的最大功率与效率。本研究可为深度强化学习在相关量子热力学问题中的深入应用提供参考。

参考文献

[1] Prielinger L, Hartmann A, Yamashiro Y, et al. Two-parameter counter-diabatic driving in quantum annealing[J]. Physical Review Research, 2021, 3(1): 013227.

[2] Guéry-Odelin D, Ruschhaupt A, Kiely A, et al. Shortcuts to adiabaticity: Concepts, methods, and applications[J]. Reviews of Modern Physics, 2019, 91(4): 045001.

[3] Hegade N N, Paul K, Ding Y C, et al. Shortcuts to adiabaticity in digitized adiabatic quantum computing[J]. Physical Review Applied, 2021, 15(2): 024038.

[4] Iram S, Dolson E, Chiel J, et al. Controlling the speed and trajectory of evolution with counterdiabatic driving[J]. Nature Physics, 2021, 17(1): 135-142.

[5] Patra A, Jarzynski C. Semiclassical fast-forward shortcuts to adiabaticity[J]. Physical Review Research, 2021, 3(1): 013087.

[6] Abah O, Paternostro M, Lutz E. Shortcut-to-adiabaticity quantum Otto refrigerator[J]. Physical Review Research, 2020, 2(2): 023120.

[7] Dupays L, Egusquiza I L, del Campo A, et al. Superadiabatic thermalization of a quantum oscillator by engineered dephasing[J]. Physical Review Research, 2020, 2(3): 033178.

[8] Funo K, Lambert N, Karimi B, et al. Speeding up a quantum refrigerator via counterdiabatic driving[J]. Physical Review B, 2019, 100(3): 035407.

[9] Li L N, Li H, Yu W L, et al. Shortcut-to-adiabaticity quantum tripartite Otto cycle[J]. Journal of Physics B: Atomic, Molecular and Optical Physics, 2021, 54(21): 215501.

[10] Hartmann A, Mukherjee V, Niedenzu W, et al. Many-body quantum heat engines with shortcuts to adiabaticity[J]. Physical Review Research, 2020, 2(2): 023145.

[11] Zhang X M, Wei Z Z, Asad R, et al. When does reinforcement learning stand out in quantum control? A comparative study on state preparation[J]. npj Quantum Information, 2019, 5: 85.

[12] He R H, Wang R, Nie S S, et al. Deep reinforcement learning for universal quantum state preparation via dynamic pulse control[J]. EPJ Quantum Technology, 2021, 8(1): 29.

[13] Sgroi P, Palma G M, Paternostro M. Reinforcement learning approach to nonequilibrium quantum thermodynamics[J]. Physical Review Letters, 2021, 126(2): 020601.

[14] Khait I, Carrasquilla J, Segal D. Optimal control of quantum thermal machines using machine learning[J]. Physical Review Research, 2022, 4(1): L012029.

[15] Erdman P A, Noé F. Identifying optimal cycles in quantum thermal machines with reinforcement-learning[J]. npj Quantum Information, 2022, 8: 1.

[16] Plastina F, Alecce A, Apollaro T, et al. Irreversible work and inner friction in quantum thermodynamic processes[J]. Physical Review Letters, 2014, 113(26): 260601.

[17] Ahmadi B, Salimi S, Khorashad A S. Irreversible work and Maxwell demon in terms of quantum thermodynamic force[J]. Scientific Reports, 2021, 11: 2301.

[18] Sivak V V, Eickbusch A, Liu H, et al. Model-free quantum control with reinforcement learning[J]. Physical Review X, 2022, 12: 011059.

李建松, 李海, 于文莉, 郝亚明. 基于深度强化学习的量子奥托循环性能优化[J]. 量子电子学报, 2025, 42(1): 70. Jiansong LI, Hai LI, Wenli YU, Yaming HAO. Performance optimization of quantum Otto cycle via deep reinforcement learning[J]. Chinese Journal of Quantum Electronics, 2025, 42(1): 70.

基于深度强化学习的量子奥托循环性能优化【增强内容出版】

0　引言

1　QOC模型

1.1　理想绝热QOC

图 1. 理想的量子奥托循环示意图

Fig. 1. Diagram of the ideal QOC

1.2　非理想绝热QOC

2　基于深度强化学习的附加驱动场优化策略

图 2. 强化学习优化附加驱动场示意图

Fig. 2. Diagram of optimization of the additional driving field by reinforcement learning

3　数值分析与讨论

3.1　能量成本和输出功

图 3. 优化附加驱动方案与自由演化方案下的能量消耗与输出功对比。(a) 能量成本 $〈C_{t o t}〉$ 与不可逆功 $〈W_{i r r}〉$ ; (b) 输出功 $W_{e d}^{t o t}$ 和 $W_{f r e e}^{t o t}$

Fig. 3. Comparison of energy cost and output work in the optimization additional driving and free evolution schemes.(a) Energy cost $〈C_{t o t}〉$ and irreversible work $〈W_{i r r}〉$ ; (b) Output work $W_{e d}^{t o t}$ and $W_{f r e e}^{t o t}$

3.2　QOC的效率和功率

图 4. 优化附加驱动方案与自由演化方案下QOC性能的对比。(a) 功率 $P_{e d}$ 和 $P_{f r e e}$ ; (b) 效率 $η_{e d}$ 和 $η_{f r e e}$

Fig. 4. Comparison of performance of QOC of the optimization additional driving and free evolution schemes.(a) Power $P_{e d}$ and $P_{f r e e}$ ; (b) Efficiency $η_{e d}$ and $η_{f r e e}$

图 5. 在 $τ = 18$ 情况下, 优化附加驱动场强度的分布特征。(a) 膨胀过程的驱动场 $f_{e d}^{e x p}$ 分布; (b) 压缩过程的驱动场 $f_{e d}^{c o m p}$ 分布

Fig. 5. Optimization distribution of additional driving field with $τ = 18$ . (a) $f_{e d}^{e x p}$ in expansion process; (b) $f_{e d}^{c o m p}$ in compression process

4　结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

基于深度强化学习的量子奥托循环性能优化【增强内容出版】

0 引言

1 QOC模型

1.1 理想绝热QOC

图 1. 理想的量子奥托循环示意图

Fig. 1. Diagram of the ideal QOC

1.2 非理想绝热QOC

2 基于深度强化学习的附加驱动场优化策略

图 2. 强化学习优化附加驱动场示意图

Fig. 2. Diagram of optimization of the additional driving field by reinforcement learning

3 数值分析与讨论

3.1 能量成本和输出功

图 3. 优化附加驱动方案与自由演化方案下的能量消耗与输出功对比。(a) 能量成本Ctot与不可逆功Wirr ; (b) 输出功Wedtot和Wfreetot

Fig. 3. Comparison of energy cost and output work in the optimization additional driving and free evolution schemes.(a) Energy cost Ctot and irreversible work Wirr ; (b) Output work Wedtot and Wfreetot

3.2 QOC的效率和功率

图 4. 优化附加驱动方案与自由演化方案下QOC性能的对比。(a) 功率Ped和Pfree ; (b) 效率ηed和ηfree

Fig. 4. Comparison of performance of QOC of the optimization additional driving and free evolution schemes.(a) Power Ped and Pfree ; (b) Efficiency ηed and ηfree

图 5. 在τ=18情况下, 优化附加驱动场强度的分布特征。(a) 膨胀过程的驱动场fedexp分布; (b) 压缩过程的驱动场fedcomp分布

Fig. 5. Optimization distribution of additional driving field with τ=18. (a) fedexp in expansion process; (b) fedcomp in compression process

4 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

0　引言

1　QOC模型

1.1　理想绝热QOC

1.2　非理想绝热QOC

2　基于深度强化学习的附加驱动场优化策略

3　数值分析与讨论

3.1　能量成本和输出功

图 3. 优化附加驱动方案与自由演化方案下的能量消耗与输出功对比。(a) 能量成本 $〈C_{t o t}〉$ 与不可逆功 $〈W_{i r r}〉$ ; (b) 输出功 $W_{e d}^{t o t}$ 和 $W_{f r e e}^{t o t}$

Fig. 3. Comparison of energy cost and output work in the optimization additional driving and free evolution schemes.(a) Energy cost $〈C_{t o t}〉$ and irreversible work $〈W_{i r r}〉$ ; (b) Output work $W_{e d}^{t o t}$ and $W_{f r e e}^{t o t}$

3.2　QOC的效率和功率

图 4. 优化附加驱动方案与自由演化方案下QOC性能的对比。(a) 功率 $P_{e d}$ 和 $P_{f r e e}$ ; (b) 效率 $η_{e d}$ 和 $η_{f r e e}$

Fig. 4. Comparison of performance of QOC of the optimization additional driving and free evolution schemes.(a) Power $P_{e d}$ and $P_{f r e e}$ ; (b) Efficiency $η_{e d}$ and $η_{f r e e}$

图 5. 在 $τ = 18$ 情况下, 优化附加驱动场强度的分布特征。(a) 膨胀过程的驱动场 $f_{e d}^{e x p}$ 分布; (b) 压缩过程的驱动场 $f_{e d}^{c o m p}$ 分布

Fig. 5. Optimization distribution of additional driving field with $τ = 18$ . (a) $f_{e d}^{e x p}$ in expansion process; (b) $f_{e d}^{c o m p}$ in compression process

4　结论