CLP Researching 中国光学期刊网 光电汇 光品汇 爱光学
红外与激光工程, 2025, 54 (4): 20250051, 网络出版: 2025-05-16  

Ф-OTDR系统中的衰落效应抑制研究进展(特邀)【增强内容出版】

Research progress of fading effect suppression in Ф-OTDR system (invited)
Get PDF
Full Text
图表
论文大纲
Metrics
More
雷艳阳 1,2陈金博 1,2刘帅旗 2李天夫 1,2董永康 1,2
作者单位
1 哈尔滨工业大学 航天学院 激光空间信息全国重点实验室，黑龙江 哈尔滨 150001
2 哈工大郑州研究院，河南 郑州 450007
相位敏感光时域反射计技术 相干衰落效应 偏振衰落效应 瑞利散射 phase-sensitive optical time-domain reflectometry interference fading polarization fading Rayleigh scattering Rayleigh scattering 
摘要
相位敏感光时域反射计（Phase-sensitive OTDR,Ф-OTDR）技术通过实时解调背向瑞利散射光信号的相位信息演变过程实现对传感光纤沿线振动/声音信号的定量测量与分析，具有响应速度快、探测灵敏度高等独特优势，在周界安防、油气管线监测、海洋监测等领域具有广阔的应用前景。但由于Ф-OTDR系统受相干衰落效应和偏振衰落效应的影响，散射信号低信噪比位置将形成传感“死区”，导致相位信息解调失真。Ф-OTDR系统结构包括自相干探测和本振外差探测两大类，常见的解调方式包括IQ相位解调、Hilbert变换解调、PGC相位解调和3×3耦合解调。现有的Ф-OTDR系统偏振衰落抑制方案主要包括全保偏系统结构、脉冲光偏振控制及偏振分集，相干衰落抑制方案主要包括波长/频率/相位分集方案、特殊传感单元方案、算法改善方案。现有的偏振、相干衰落抑制方案均有效改善了Ф-OTDR系统中传感“死区”导致的相位解调失真，实现了对振动信号的高保真定量测量。随着Ф-OTDR系统应用领域的不断拓展，高解调速率、多参量融合感知将是未来Ф-OTDR技术的研究趋势。
Abstract
Significance Phase-sensitive optical time-domain reflectometry (Ф-OTDR) represents a significant branch of distributed fiber sensing technology. This technique facilitates the quantitative analysis of vibration and acoustic signals along the sensing fiber by real-time demodulation of the phase evolution of backscattered Rayleigh light. It is distinguished by its rapid response and high detection sensitivity, making it particularly suitable for applications such as perimeter security, oil and gas pipeline leak detection, and marine monitoring. However, owing to the utilization of a narrow line-width laser light source in the Ф-OTDR system, the Rayleigh scattered light signal generated within the sensing fiber exhibits high coherence. This results in random fluctuations of the Rayleigh scattered light signal along the sensing fiber due to interference between scattered light, thereby creating sensing dead zones at positions with low signal-to-noise ratios. Additionally, polarization mismatch between the Rayleigh backscattered light signal and the local reference light further contributes to these sensing dead zones, leading to phase demodulation distortion. In recent years, suppressing the fading effect in Ф-OTDR systems has emerged as a research hotspot, with significant academic and practical importance.Progress The Ф-OTDR system includes two main types of structures: self-coherent detection and intrinsic heterodyne detection. Common demodulation methods include IQ phase demodulation, Hilbert transform demodulation, PGC phase demodulation, and 3 × 3 coupling demodulation. The existing polarization fading suppression schemes for the Ф-OTDR system primarily encompass three approaches: Ф-OTDR system mainly consist of three approaches: Full polarization maintenance, probe pulse polarization control, and polarization diversity. The full polarization maintenance approach entails significant structural costs and demonstrates low cost-effectiveness in long-distance engineering monitoring applications. The probe pulse polarization control method requires complex modulation of optical signals within the Ф-OTDR system. In contrast, the polarization diversity scheme only necessitates implementing diversity at the receiving-end optical path, effectively mitigating partial fading while offering a simpler structure and lower costs. Therefore, it is currently the most prevalent solution for Polarization fading suppression.The fundamental principle of interference fading suppression involves generating and synthesizing multiple independent signals with low correlation in order to accurately demodulate high-fidelity phase information. The primary approaches encompass wavelength, frequency, or phase diversity, specialized sensing units, and algorithmic enhancements. The frequency, phase, or wavelength diversity scheme realizes interference fading suppression based on the different Rayleigh scattering distribution characteristics of probe pulses with different frequencies, phases or wavelengths, it is a pioneering and most widely adopted interference fading suppression schemes. The special sensor unit scheme uses multi-mode fiber, few-mode fiber, multi-core fiber and scattering enhanced fiber as the sensor units of the Ф-OTDR system to obtain multiple independent signals with low correlation or a stable Rayleigh scattering distribution, which is one of the effective means to realize interference fading suppression without necessitating complex optical path. The algorithmic enhancement scheme does not require complex probe pulse modulation and special sensing units, and only performs signal processing in the digital domain to achieve high-fidelity phase information demodulation. The classical algorithms include spectrum extraction and remixing, phase shift transformation, rotation vector sum method, etc.Conclusions and Prospects Researchers have proposed and validated numerous schemes to suppress polarization and interference fading effects, which significantly mitigate phase demodulation errors caused by fading in the Ф-OTDR system. This has facilitated the application of Ф-OTDR technology in industrial monitoring. With the continuous expansion of the application field of Ф-OTDR technology, end-users are imposing increasingly stringent requirements on this technology. In the future, real-time demodulation of vibration or acoustic information along the sensing fiber will be of critical importance. This is because the machine-OTDR system generates a substantial volume of data during high-frequency signal monitoring or long-distance monitoring. Furthermore, the distributed optical fiber sensing system, which supports multi-parameter hybrid measurement, is anticipated to offer significant advantages in the realm of industrial monitoring in the future.

0 引　言

光纤中的散射效应是由纤芯介质折射率分布不均匀引起的一种弹性散射现象，散射过程仅入射光的方向和能量发生改变，背向瑞利散射（RBS）光信号的散射率约为−70 dB/m[1]。光时域反射技术（Optical Time Domain Reflectometry, OTDR）是基于瑞利散射效应的首项分布式光纤传感技术，该技术于1976年，由 BAMOSKI M K等人借鉴激光雷达的概念提出，并成功应用于对传感光纤链路损耗的检测[2]。1982年，HEALEY P等人将窄线宽光源引入OTDR系统中，并采用相干探测结构，实现相干OTDR（Coherent OTDR, COTDR）系统，有效改善了系统的信噪比[3]。1984年，HEALEY P等人首次发现COTDR系统中的相干衰落效应，将RBS光信号的波动起伏分布认定为相干衰落噪声[4]。1993年，TAYLOR H F 等人将相干衰落噪声理解为一种有用信号，并提出相位敏感光时域反射计（Phase-sensitive OTDR, Ф-OTDR）系统[5]。随后十余年里，随着窄线宽激光光源的成熟，Ф-OTDR技术逐渐成为研究热点，并得到了蓬勃发展，在周界安防、油气管线监测、海洋监测等领域成功应用并表现其独特的技术优势[6-11]。现已成为分布式光纤传感技术的重要分支之一。

根据解调方式的不同，Ф-OTDR技术可进一步细分为解调RBS光信号强度信息的分布式振动传感（DVS）系统[12-15]和解调RBS光信号相位信息的分布式声波传感（DAS）系统[16-20]；由于RBS信号的强度变化与振动导致的光纤形变没有线性数学关系，DVS系统通常用于对传感光纤沿线振动信号的定性分析；而DAS系统的优势在于，RBS信号的相位变化与振动信号导致的光纤形变具有明确的线性数学关系，可实现对振动/声音信息的定量还原。然而，高相干光脉冲注入折射率分布不均匀的传感光纤中后，产生的RBS光信号在光脉冲半宽范围内相干叠加，相干相消位置将具有较低的信噪比，在解调相位信息时将引起较大的解调误差，从而形成传感“死区”，恶化DAS系统的传感性能。其次，RBS光信号与本振参考光之间的偏振态失配也会导致传感“死区”。近年来，DAS系统中的衰落效应抑制一直是研究热点，大量的解决方案相继涌现，推动DAS技术更好地服务于工业领域。

文中先对Ф-OTDR系统的工作原理及常见的系统结构及解调算法[21-24]进行描述归纳，再对Ф-OTDR系统中偏振衰落解决方案进行简要概述[25-40]；然后重点回顾和总结现有Ф-OTDR系统中相干衰落抑制技术[41-108]的研究进展；最后，对Ф-OTDR系统的未来发展趋势进行展望。

1 Ф-OTDR的传感原理及主要结构

在Ф-OTDR系统中，当传感光纤沿线外界振动事件导致光纤产生周期性微小形变时，导致光纤中传播的光波信号光程差改变，从而表现为振动事件对光波信号相位信息的调制；由于光波相位信息随传感距离线性累加，通过实时解调振动区域前、后属于稳定状态的两个参考点之间RBS光信号的相位信息变化过程即可实现对振动事件的定量还原。在图1（a）所示的系统空间分辨率模型中，载频为$ {f_0} + \Delta f $、距离域宽度为W的探测脉冲光注入传感光纤中，当探测脉冲光的前沿在位置B处产生RBS光信号时，位置A对应探测脉冲光的中间位置；当探测脉冲光的后沿到达位置A时，在位置A产生的RBS光信号与位置B处返回的RBS光信号相遇，并发生干涉叠加；因此传感光纤任意位置A处的RBS光信号为探测脉冲光W/2尺度上A、B两点散射光信号的干涉叠加结果；也即探测脉冲光距离域宽度决定了系统的空间分辨率W/2；在定量解调传感光纤沿线振动事件时，距离域相位差的求解间距通常等于空间分辨率。

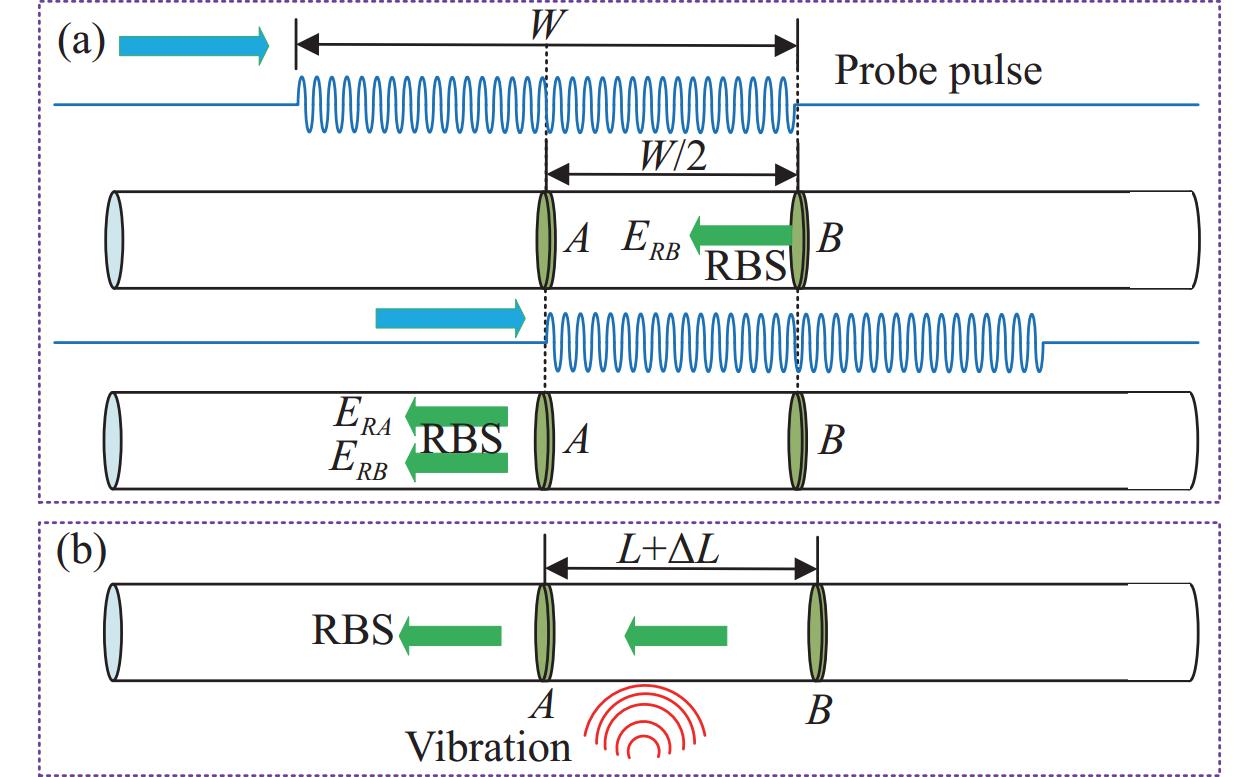
图 1. (a) 空间分辨率模型；(b) 振动传感模型

Fig. 1. (a) Spatial resolution model; (b) Vibration sensing model

下载图片 查看所有图片

在如图1（b）所示的振动传感模型中，传感光纤未受外界振动影响时，距离间隔为L的两个参考点A和B处的RBS信号表示如下：

$ \left\{ {\begin{array}{*{20}{c}} {{E_{RA}} = {E_A}\cos \left[ {\left( {\omega + \Delta \omega } \right)t + {\varphi _1}} \right] } \\ {{E_{RB}} = {E_B}\cos \left[ {\left( {\omega + \Delta \omega } \right)t + {\varphi _1} + \dfrac{{4n\pi }}{\lambda }L} \right]} \end{array}} \right. $ (1)

式中：ω和$ \Delta \omega $分别表示光源的角频率和探测脉冲光的频移；$ {E_A} $和$ {E_B} $分别表示参考点A和B两个位置的RBS光信号幅值；$ {\varphi _1} $为参考点A处的初始相位信息；$ \lambda $表示光波波长；n表示传感光纤有效折射率。此时，参考点A和B之间的RBS光信号相位差$ \Delta {\varphi _{AB}} $可以表示为：

$ \Delta {\varphi _{AB}} = \frac{{4n\pi }}{\lambda }L $ (2)

当传感光纤受外界振动影响时，传感光纤上两个参考点A和B之间产生$ \Delta L $的形变；忽略折射率变化产生的影响，参考点A和B之间的相位差$ \Delta {\varphi _{ABvibration}} $可以表示为：

$ \Delta {\varphi _{ABvibration}} = \frac{{4n\pi }}{\lambda }\left( {L + \Delta L} \right) $ (3)

综上所述，参考点A和B之间振动事件引起的相位差变化为$ \Delta {\varphi _{ABvibration}} - \Delta {\varphi _{AB}} $。

常见的Ф-OTDR系统可根据系统结构的不同，分为自相干探测方式和本振外差探测方式两大类，如图2所示；图2（a）~（d）为四种不同结构的自相干探测系统，通常采用不同频率/不同相位的双脉冲对或延时结构使得公式（1）中两个参考点的散射光信号重叠，从而发生干涉效应，干涉光信号进一步表示如下：

图 2. (a) 双脉冲对型；(b) 二端口-迈克尔逊干涉仪 (MI) 型；(c) 三端口-马赫-曾德干涉仪 (MZI) 型；(d) 三端口-迈克尔逊干涉仪 (MI) 型；(e) 本振外差探测型 (常规脉冲)；(f) 本振外差探测型 (啁啾脉冲)

Fig. 2. (a) Double pulse type; (b) Two-port Michelson Interferometer (MI) type; (c) Three-port Mach-Zender interferometer (MZI) type; (d) Three-port Michelson Interferometer (MI) type; (e) Heterodyne detection type (conventional pulse); (f) Heterodyne detection type (chirp pulse)

下载图片 查看所有图片

$ {I_{{{self\text{-}c}}}} = {E_A}^2 + {E_B}^2 + 2{E_A}{E_B}\cos \left( {\frac{{4n\pi }}{\lambda }L} \right) $ (4)

图2（e）和（f）均为本振外差探测结构，区别在于图2（e）的探测脉冲光为固定频率的短脉冲，空间分辨率取决于脉冲光宽度，而图2（f）的探测脉冲光为频率线性扫描的长啁啾脉冲，空间分辨率取决于扫频范围，打破了传感距离与空间分辨率的制约关系。本振外差探测方式引入本振光分别与公式（1）中两个参考点的散射光信号进行相干，相应的本振光电场表达式如下：

$ {E_{Lo}} = {E_L}\cos \left( {\omega t + {\varphi _0}} \right) $ (5)

式中：$ {E_L} $表示本振光信号幅值；$ {\varphi _0} $为本振光的初始相位信息；相干拍频后的光信号可表示如下：

$ \left\{ {\begin{array}{*{20}{c}} {{I_{LoRA}} = {E_L}{E_A}\cos \left[ {\Delta \omega t + {\varphi _1} - {\varphi _0}} \right] \quad \quad \quad } \\ {{I_{LoRB}} = {E_L}{E_B}\cos \left[ {\Delta \omega t + {\varphi _1} - {\varphi _0} + \dfrac{{4n\pi }}{\lambda }L} \right]} \end{array}} \right. $ (6)

上述分析成立的前提是图2（f）所示的使用啁啾脉冲的系统，即基于时间门控-光频域反射计（TGD-OFDR）系统，将啁啾脉冲压缩成中心频率为$ \omega + \Delta \omega $的等效单频脉冲。总之，本振外差探测方式的显著优势在于引入本振光对瑞利散射信号光做一次外差放大，有效提高信噪比，具有较长的传感距离。

解调公式（5）和（6）中两个参考点A和B之间的相位差信息需要借助不同的解调算实现，根据解调算法的不同，主要可分为：3×3耦合解调[21]、PGC相位解调[22]、IQ相位解调[23]和Hilbert变换解调[24]。其中，IQ相位解调和Hilbert变换解调适用于图2（a）、图2（e）和图2（f）所示的脉冲对自相干探测型结构和外差探测型结构，PGC相位解调适用于图2（b）所示的二端口-迈克尔逊干涉仪（MI）型；3×3耦合解调适用于图2（c）和图2（d）所示的三端口-马赫-曾德干涉仪（MZI）型和三端口-迈克尔逊干涉仪（MI）型。上述四种相位解调算法各有优劣，IQ相位解调和Hilbert变换解调的结构最为简单，IQ相位解调具有高信噪比和高灵敏度，但只适用于本振外差相干探测，且需要在数字域产生与待解调信号同频正交和同频同相的两路参考信号；Hilbert变换解调额外适用于脉冲对直接探测和零差相干探测结构，但易受慢变噪声影响；PGC解调和3×3耦合解调对光路结构的稳定性要求较高，对温度和振动较为敏感，但不易受偏振态失配影响。

2 Ф-OTDR系统中的衰落效应

2.1 偏振衰落效应

Ф-OTDR系统中的偏振衰落效应源于单模传感光纤中存在的双折射现象[25]，光纤中传输的光脉冲信号偏振态随机变化，引起RBS光信号与本振参考光信号的偏振态不一致，导致拍频信号的幅值随机涨落；当偏振态失配较为严重时，影响Ф-OTDR系统相位解调的准确性，恶化传感性能。目前，抑制偏振衰落的有效技术手段主要有全保偏结构传感系统[26]、脉冲光偏振控制[27-31]、偏振分集方案[32-39]；此外，安阳等人采用基于琼斯矩阵的双光束干涉Ф-OTDR系统，抑制偏振衰落噪声[40]。全保偏结构传感系统成本和传输损耗都较高，不适用于长距离传感领域的应用，偏振分集方案应用较为广泛。

2.2 相干衰落效应

相干衰落效应作为Ф-OTDR系统的技术痛点及研究热点之一，研究人员提出并演示了大量的解决方案；核心思想是通过各种方式产生并合成多个低相关度的独立信号，对相干衰落效应导致的解调“死区”互补，从而实现时-空域双维度的高保真相位信息解调；主流的技术方案可归纳为：频率分集方案[41-65]、相位分集方案[66-69]、波长分集方案[70-72]、特殊传感单元（多模[73-75]、少模光纤[76-79]、多芯光纤[80-82]、散射增强光纤[31, 83-87]、特殊结构[88-89]等）方案、算法补偿方案[90, 108]。

2.2.1 频率/相位/波长分集方案

基于频率/相位/波长分集抑制Ф-OTDR系统中的相干衰落效应是最早且最主流的技术方案，主要利用不同频率/相位/波长探测脉冲光在传感光纤中具有不同的瑞利散射分布，即散射信号弱相关的特性，通过各种聚合方式实现衰落位置的补偿；该类技术方案主要通过对探测光脉冲的复杂调制实现。

2012年，张旭萍等人提出了一种基于多频脉冲的Ф-OTDR，采用功率相同的3个频率作为探测脉冲[41]；与传统单频Ф-OTDR相比，该方案的测量次数可增加3倍，具有快速衰落噪声抑制能力。同年，蔡海文等人提出了一种相移双脉冲Ф-OTDR方案，将脉冲内随机干涉转化为可控脉冲间干涉，通过对两个相反干涉信号的幅值和相位的综合分析，以减少相干衰落对相位解调的影响[66]。2013年，蔡海文等人最早证明了Ф-OTDR系统中相干衰落点位置随探测脉冲光的载频改变[42]，部分结果如图3所示。同年，该团队在此项工作的基础上提出一种基于多频率综合判决的方法[43]，即选用3个拍频信号对应位置幅度最大的用作相位解调。自此，各种基于频率/波长分集的解决方案纷纷涌现。

图 3. 不同频率的拍频信号[42]

Fig. 3. Beat signals of different frequency [42]

下载图片 查看所有图片

2017年，刘庆文等人提出一种TGD-OFDR的无相干衰落噪声DAS系统[44]，如图4所示；系统中使用微秒级的啁啾脉冲，在数据处理时采用脉冲压缩的方式实现等效DAS系统，该系统中首次提出内脉冲分频法将啁啾脉冲频谱压缩为具有不同中心频率的等效单频脉冲，并使用旋转矢量和法（RVS）来合成多个独立信号，有效抑制相干衰落导致的相位噪声；如图5所示，RVS的本质是将不同独立信号解调的相位进行加权平均，权重为对应位置独立信号的幅值大小。

图 4. 实验装置[44]

Fig. 4. Experimental setup[44]

下载图片 查看所有图片

图 5. RVS原理[44]。(a) 两个复矢量求和；(b) 不施加应变的RVS；(c) 施加应变的RVS

Fig. 5. Schematic of RVS [44]. (a) Addition of two complex vectors; (b) RVS without strain; (c) RVS with strain

下载图片 查看所有图片

2018年，HARTOGA H 等提出并验证了在Ф-OTDR系统中引入一个特殊的光学环路，产生具有不同时间延迟和载频的脉冲序列抑制相干衰落[45]。同年，刘庆文等提出一种基于强度调制器（IM）的TGD-OFDR系统[46]；在保持空间分辨率不变的情况下，充分利用正、负谐波来抑制衰落。同年，孟洲等利用三波长方案来降低基于相位产生载波算法（PGC）解调的自外差相干Ф-OTDR系统中的衰落噪声[70]。2019年，王子南等从理论上描述并实验验证了在任意数目的独立探测通道下，如何抑制一维光散射中的衰落现象[47]。同年，张旭萍等人利用3个不同载频的AOM调制多载频的探测光脉冲，并提出了一种在任意时刻选择最佳探测信号的跟踪算法，有效抑制相干衰落[48]。朱涛等人采用三载频脉冲，结合非线性频率调制技术在80 km的传感距离上实现高保真解调[49]。蔡海文等人通过差分相移脉冲技术（DPSP），使得Ф-OTDR系统中的相干衰落变得可控[67]，通过参考幅度阈值解调保真相位信息。2021年，饶云江等人提出了双极Golay编码的Ф-OTDR来解决扫描速率问题，通过一种新的实时补偿方法补偿激光频率漂移，并结合频谱提取和混合方法消除干扰衰落[50]。周娴等人提出了频谱提取和旋转矢量和（SERVS）方法来抑制脉冲强度编码Ф-OTDR中的相干衰落[68]。蔡海文等展示了一种基于波长分集的Ф-OTDR系统，利用差分矢量聚合方法降低信号衰落[51]。OGDEN H M等人提出了一种频率复用的Ф-OTDR系统[52]，使用一系列频移脉冲注入传感光纤并在接收端使用偏振分集，该方法降低噪声和减轻相干衰落的同时提高了传感器的线性度。LOAYSSA A等人提出了一种双波长Ф-OTDR系统，使用完美的周期性相关相位码来增强测量性能，实现相干和偏振衰落的同时补偿[71]。IIDA D等提出一种在时域和频域上旋转并平均复矢量的双平均方法，结合频分复用的Ф-OTDR系统抑制相干衰落[53]。随后，IIDA D等在该工作的基础上调制时序脉冲序列提升Ф-OTDR系统的响应带宽[54]。

2022年，靳宝全等提出一种主动频率变换（AFT）方法，解决Ф-OTDR系统中相干衰落抑制不彻底的问题[55]。孙琪真等人建立了频率、偏振和初始相位独立的双激光器辅助Ф-OTDR系统，同时抑制由脉冲内部干涉、偏振失配和相位失配引起的衰落现象[72]。王子南等人首次将失配滤波引入到外差Ф-OTDR中，解决扫描速率和相干衰落问题[69]。2023年，唐明等人提出一种频率响应增强的无衰落Ф-OTDR系统[56]，该系统利用EOM和AOM调制产生同时携带3个载频且周期随机的探测光脉冲，突破传统Ф-OTDR系统传感范围和响应带宽之间的权衡，且通过RVS抑制相干衰落。笔者团队提出利用相位调制光频率梳来抑制Ф-OTDR中的相干衰落效应[57]，演示实验中调制了图6所示的7个频率梳，并对衰落抑制效果进行评估。

图 6. (a) 7个频率分量；(b) 概率密度分布[57]

Fig. 6. (a) Seven frequency components; (b) Probability density distribution [57]

下载图片 查看所有图片

2024年，笔者团队提出一种基于宽带声光调制的高保真Ф-OTDR传感方案，实现对振动信号相位信息的高保真提取[58]。靳宝全等人提出基于频移延迟环（FSDL）的无衰落DAS方案[59]，如图7所示；引入分段聚集近似（PAA）来压缩运算数据量，采用小波能量谱分析和支持向量机（SVM）进行特征提取，实现衰落分类；该算法通过衰落标记的生成和恢复，利用RVS算法对多频信号进行聚合。

图 7. 基于FSDL的Ф-OTDR实验装置[59]

Fig. 7. Ф-OTDR experimental setup based on FSDL[59]

下载图片 查看所有图片

随后，该团队在频移延迟环（FSDL） DAS系统的基础上通过构造BP神经网络模型实现衰落状态识别，并利用RVS算法对非衰落信号进行聚合[60]。吴宇等人提出一种基于多频优化分集（MFOD）算法的Ф-OTDR系统[61]，MFOD算法能够较好地还原相位信息和提升信噪比（SNR）。何祖源等人在基于TGD-OFDR的DAS系统中引入移频环，在不牺牲空间分辨率的情况下实现衰落噪声抑制和高频响应[62]。沈永行等人提出了一种新的无衰落DAS结构，该结构通过在双脉冲自外差DAS系统中引入声光频移（AOFS）环路来实现[63]。李朝晖等人演示了一种通过实施三层结构复用（TLSM）技术来减轻Ф-OTDR系统中衰落影响的方法[64]；TLSM方法基于多脉冲检测、频谱分割和空间复用来创建独立的拍频信号，然后通过RVS方法重新合成；并采用卡尔曼滤波器来消除这些独立拍频信号之间的相位失配。饶云江等人提出了一种基于双频率梳相干并行的DAS概念，系统如图8所示。通过在相干型DAS系统中引入一对克尔孤子微腔频率梳，实现传感信号线性叠加的同时减轻了光源噪声；通过对孤子对重复频率差的精细控制，实现了高精度的频分复用相位解调。该方案具有巨大的灵敏度增强潜力和较高的受激布里渊散射阈值，有利于延长DAS系统的传感距离[65]。

图 8. 基于双频率梳的DAS实验装置[65]

Fig. 8. DAS experimental setup based on dual frequency comb[65]

下载图片 查看所有图片

2.2.2 特殊传感单元方案

利用多模光纤（MMF）、少模光纤（FMF）、多芯光纤（MCF）、散射增强光纤（SEF）等特殊光纤代替普通单模光纤（SMF）作为DAS系统的传感单元，获得多个低相关度的独立信号或稳定的瑞利散射分布；并通过模分复用（MDM）、空分复用（SDM）、时分复用（TDM）等方式合成独立信号，是实现DAS系统中相干衰落效应抑制的有效手段之一。同时，飞秒/紫外刻写散射增强光纤（SEF）作为近年来的热门技术，备受广大研究者的喜爱和关注。以下为利用特殊传感单元作为DAS传感单元，实现高保真相位信息解调的经典解决方案的总结：

2016年，ALEKSEEVA E 等人首次证明了利用多模光纤作为Ф-OTDR系统的传感单元消除相干衰落的可能性[73]。2018年，王峰等人演示了一种基于超弱光纤光栅（UWFBG）阵列辅助的双脉冲Ф-OTDR系统[83]，由于传感单元具有稳定的瑞利散射，相干衰落位置可控。樊昕昱等人提出了一种高性能的准分布式光纤声传感系统[84]，系统中采用辅助干涉仪降低激光相位噪声的影响，并引入偏振分集与UWFBG阵列，同时避免了相干和偏振衰落的影响。2019年，王峰等人提出一种使用复合双探测脉冲（CDPP）来消除基于UWFBG阵列的DAS系统中衰落效应的方案[31]。陈勐勐等人提出了一种基于MCF进行SDM的Ф-OTDR系统，并基于频谱相似度的策略来处理得到的多个独立信号，实现衰落抑制[80]。2019年，MASOUDI A等人介绍了一种基于双模光纤的Ф-OTDR[76]，通过结合从不同模式获得的结果，实现相干衰落噪声的改善。

2020年，闫志君等人提出一种基于空心圆柱形结构传感单元的Ф-OTDR系统，将包含若干BEP的微结构光纤（DMOF）用于提高SNR，避免相干衰落；并构造空心圆柱形结构增强声信号检测灵敏度[85]。REDDING B 等人提出了一种基于SEF的低噪声DAS[86]，该传感系统具有较高的线性度，且不受相干衰落的影响。

2021年，唐明等人提出了基于FMF进行SDM的Ф-OTDR方案[77]；探测脉冲由三种不同的空间模式（LP01、LP11a和LP11b）组成，如图9所示；并以振幅强度的−10 dB为衰落阈值对使用单模式探测脉冲和多模式探测脉冲的Ф-OTDR系统的性能进行了比较和评估，传感光纤的距离（4.85 km）和时间（1600 s）两个尺度上无低于衰落阈值的点。

图 9. 基于少模光纤的Ф-OTDR系统实验装置[77]

Fig. 9. Experimental setup of the few-mode fiber based Ф-OTDR system[77]

下载图片 查看所有图片

同年，蔡海文等人分析了影响Ф-OTDR系统信噪比的因素，并利用FMF的高捕获效率、高非线性阈值和多通道独立传输的优点，提出一种采用多横向模式集成（MTMI）技术的Ф-OTDR系统，有效地抑制相干衰落，降低本底噪声[78]。同年，该团队采用了一种特殊设计的光纤结构来缩小孔径，对于来自多达约100个信道的信号进行合成，消除相干衰落[88]。2022年，该团队提出一种FMF的超低噪声多输入多输出（MIMO） DAS系统，通过MIMO技术，系统可实现更高的分集规模，获得更大的信噪比增益[79]。ORSUTI D等人利用MMF作为DAS系统的传感单元，估计不同独立信号之间的最佳旋转角度，改进RVS方法，抑制相干衰落[74]。随后在文献[75]中对该工作进行详细阐述。

2023年，沈平等人提出了一种基于MCF的Ф-OTDR系统，利用MCF的两芯用于传感，将独立的后向散射信号解调结果通过互相关算法消除衰落引起的误报[81]。同年，沈平等人演示了在基于MCF的Ф-OTDR系统中结合SDM和FDM技术，实现衰落抑制和增强信号[82]。2024年，HOCINE M 等人采用多根光纤首尾互连形成单根蛇形光纤作为DAS系统的传感单元，通过聚合所有光纤段对应的信号实现降噪[89]。2025年，张旭萍等人提出一种基于双波长超弱光纤布拉格光栅（UWFBG）阵列的新型DAS[87]；如图10所示，阵列中的UWFBG具有两个交替排列的波长，两个具有不同波长和交错发射时间的双脉冲用于传感；该方法成功地克服了传统基于UWFBG的DAS中空间分辨率和传感距离之间的权衡，并有效地将受传感距离约束的最大可实现采样率提高了一倍，时分多路复用避免了不同波长的串扰。

图 10. 基于交替排列的双波长UWFBG阵列的波长复用双脉冲DAS实验装置[87]

Fig. 10. The phase demodulation and synthesis process of wavelength multiplexed double-pulse DAS based on an alternating arranged dual-wavelength UWFBG array[87]

下载图片 查看所有图片

2.2.3 算法改善方案

通过改进相位解调算法，实现Ф-OTDR系统中相干衰落的抑制，是一种经济有效的技术手段，不需要复杂的波长/相位/频率调制与复用或特殊的传感单元，仅在数字域中执行的信号处理，实现高保真相位解调。

2016年，王廷云等人提出了一种比较Ф-OTDR系统中报警峰值前、后传感光纤位置解调的相位信息，区分衰落和真实振动报警峰值[90]。2019年，王子南等人提出一种的频谱提取和混合（SEMS）方法，实现无相干衰落的Ф-OTDR系统[91]；该方法通过切割如图11所示的单个矩形探测脉冲的频谱内容，获得多条独立信号，并以RVS的方式聚合。

图 11. 矩形脉冲频谱提取过程[91]

Fig. 11. Spectrum extraction process of rectangular pulses[91]

下载图片 查看所有图片

2020年，俞本立等人针对封装式特征选择算法中时间复杂度最高的问题，提出了一种基于最近邻分析的统计方法，对每次测量信号分离，评估并选择子分离的相位以重构振动，实现Ф-OTDR系统中的衰落抑制[92]。古利娟等人证实了相干衰落噪声的统计特性以及恢复后的相位信号的功率谱密度和均方根误差之间的反相关关系，提出一种优化的实时加权算法抑制衰落噪声[93]。张益昕等人提出了一种基于RBS相位与幅度的数值关系和抑制掩模的Ф-OTDR系统衰落虚警抑制方法[94]。刘铁根等人提出了基于LFM脉冲的虚拟块阵列空间差分相位提取方法，解决了干涉衰落的影响和信噪比差的 问题[95]。2021年，张旭萍等人提出了一种简单有效的最优寻峰算法，抑制Ф-OTDR系统中的相干衰落[96]；随后又提出了一种基于锁相结构的相干Ф-OTDR系统[97]，该系统具有较强的抗衰落能力，可以为振动重建提供更高的精度。何海军等人提出了一种相移变换方法（PST）抑制Ф-OTDR系统中的相干衰落[98]，获得高保真相位信息解调。

2022年，何海军等人提出一种数字域多频分集方案抑制Ф-OTDR中的相干衰落[99]，通过对拍频信号进行短时傅里叶变换（STFT），充分利用单频脉冲的频谱内容并在时频域中分解，而无需牺牲更多的空间分辨率。孙琪真等人提出时空联合过采样-下采样技术抑制Ф-OTDR系统的噪声[100]，空间过采样用于人为密集采样，其间隔远小于目标空间分辨率；然后将多个差分子向量的平均值进行空间下采样，以减少噪声向量的影响，从而消除相干衰落。罗斌等人分析了Ф-OTDR中衰落引起的解调假相位峰与被测信号信噪比之间的定量关系，提出一种移动旋转矢量平均（MRVA）方法，在空间分辨率损失较小的情况下实现高保真相位解调[101]。

2023年，渠帅等人提出了基于时频域联动的形态成分分析（MCA）方法来减轻相干衰落的影响并提高DAS系统的性能[102]，与传统的二维均值滤波（MVF）和二维小波变换（WT）方法相比，在不损害传感光纤沿线信源信息的前提下，消除了相干衰落引起的异常信息。张福东等人提出一种基于遗传算法和变分模式分解（VMD）的Ф-OTDR衰落噪声抑制方法[103]。随后，张福东等人又提出一种基于非局部均值滤波的Ф-OTDR系统衰落抑制方法[104]，在保持目标事件信号特征的同时，有效抑制信号中的系统衰落噪声，提高信噪比。张天瑜等人提出一种基于幅度的衰落自适应掩蔽和掩蔽自动编码（FAM-MAE）算法[105]，对幅度信号进行微分计算和分析，采用带噪声的密度聚类算法（DBSCAN）确定Ф-OTDR系统衰落点的位置，利用MAE重构这些位置以实现衰落抑制。

2024年，邵理阳等人提出了综合衰落抑制（IFS）算法集的概念，演示系统如图12所示。该算法集包含如图13所示的四种去噪方法，每种方法至少由两种独立的去噪技术组成，多个单域去噪方法的结合提高了该方法的可靠性[106]。

图 12. 实验系统结构[105]

Fig. 12. Experimental setup[105]

下载图片 查看所有图片

图 13. 处理方法比较[105]。 (a) BPF；(b) SERM；(c) PST；(d) MRVA；(e)~(h) IFS

Fig. 13. Processing methods for comparison[105]. (a) BPF; (b) SERM; (c) PST; (d) MRVA; (e)-(h) IFS

下载图片 查看所有图片

随后，该团队又提出一种基于时域拼接和复域滑动平均的快速信号合成（FSS）算法，该算法能够在保持衰落抑制性能的同时快速合成信号[107]。同年，靳宝全等人提出了一种基于容错卡尔曼滤波器的多传感器信息融合算法[108]。苑立波等人研究了一种基于双光束Ф-OTDR和四芯光纤的矢量分布式振动传感方法，数据处理时选择两个相干衰落影响较小的位置以计算相位差，从而获得更好的结果[109]。施羿等人在直接检测Ф-OTDR的解调过程中发现所选时域传感序列之间的相关性过大会导致一定时长内的相位解调失败；此外，在解调过程中存在相位极性翻转现象，进一步降低解调相位的质量。为了获得真实的外部入振动起的相位变化，提出了一种基于瑞利后向散射时间序列信息冗余的多位置补偿高质量相位解调策略；通过计算时间感知序列之间的互相关来选择最佳解调位置[110]。

3 展　望

为有效抑制Ф-OTDR系统中的偏振和相干衰落效应，实现高保真振动定量解调，国内外众多科研团队提出大量有效的解决方案；例如，用于抑制偏振衰落的全保偏结构、脉冲偏振控制、偏振分集等方案，用于抑制相干衰落的多波长/多相位/多频率/多空间复用、散射增强光纤、算法优化等方案。未来，具高保真定量振动解调能力的Ф-OTDR传感系统仍具有广阔的研究和发展空间，例如：

1）高解调速率的Ф-OTDR传感系统，虽然Ф-OTDR系统相较于基于布里渊散射的分布式光纤传感系统，具有较高的响应速率；但在具有长距离或高测量速率要求的应用场景中，利用多独立信号解决相干衰落的同时，庞大的数据量对实时数据运算解调带来巨大考验。所以，实现高保真定量解调的同时如何满足实时解调的应用需求尤为关键。

2）多参量融合分析，Ф-OTDR传感系统线性测量的振动信息，具有一定的片面性，往往不能满足复杂应用场景的监测需求，如何在有限的调制资源和频谱资源下实现多参量传感高度融合，更为全面的感知和解耦多因素共同作用的事件极为迫切。

4 结　论

文中简单回顾了基于瑞利散射的时域分布式光纤传感技术的发展历程及用于定量测量的Ф-OTDR系统的工作原理、系统结构及解调算法。针对Ф-OTDR中的衰落效应导致传感解调“死区”这一研究热点，简要概述由RBS光信号与本振参考之间偏振态失配导致的偏振衰落解决方案；重点回顾和总结国内外解决Ф-OTDR系统中相干衰落的技术方案，包括多波长/多频率/相位复用、散射增强光纤及算法优化等主流方案。最后，对Ф-OTDR系统的未来发展趋势进行展望。

参考文献

[1] 路阳, 李俐凡, 黄秋阳, et al. 准分布式声波传感系统瑞利散射串扰抑制技术[J]. 光学学报, 2024, 44(1): 231568.

    LU Y, LI L F, HUANG Q Y. Reducing crosstalk induced by Rayleigh backscattering light-waves in a quasi-distributed acoustic sensing system[J]. Acta Optica Sinica, 2024, 44(1): 231568.

[2] BARNOSKI M K, JENSEN S M. Fiber waveguides: A novel technique for investigating attenuation characteristics[J]. Applied Optics, 1976, 15(9): 2112-2115.

[3] HEALEY P, BOOTH R C, DAYMOND-JOHN B E, et al. OTDR in single-mode fibre at 1.5 μm using homodyne detection[J]. Electron Lett, 1984, 20(9): 360-362.

[4] HEALEY P. Fading in heterodyne OTDR[J]. Electronics Letters, 1984, 20(1): 30-32.

[5] Tayl H F, Lee C E. Apparatus method f fiber optic intrusion sensing: US, 5194847[P]. [2025114].

[6] 张旭苹, 丁哲文, 洪瑞, et al. 相位敏感光时域反射分布式光纤传感技术[J]. 光学学报, 2021, 41(1): 0106004.

    ZHANG X P, DING Z W, HONG R. Phase sensitive optical time-domain reflective distributed optical fiber sensing technology[J]. Acta Optica Sinica, 2021, 41(1): 0106004.

[7] 吴慧娟, 刘欣雨, 饶云江. 基于Φ-OTDR的光纤分布式传感信号处理及应用[J]. 激光与光电子学进展, 2021, 58(13): 39-59.

    WU H J, LIU Y X, RAO Y J. Processing and application of fiber optic distributed sensing signal based on Ф-OTDR[J]. Laser & Optoelectronics Progress, 2021, 58(13): 39-59.

[8] DALEY T M, FREIFELD B M, AJO-FRANKLIN J, et al. Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring[J]. The Leading Edge, 2013, 32(6): 936-942.

[9] 杨震, 封皓. 基于深度学习的Φ-OTDR输油管道入侵监测研究[J]. 激光与光电子学进展, 2022, 59(8): 51-59.

    YANG Z, FENG H. Oil pipeline intrusion monitoring based on deep learing of Ф-OTDR[J]. Laser & Optoelectronics Progress, 2022, 59(8): 51-59.

[10] LIOKUMOVICH L B, USHAKOV N A, KOTOV O I, et al. Fundamentals of optical fiber sensing schemes based on coherent optical time domain reflectometry: Signal model under static fiber conditions[J]. Journal of Lightwave Technology, 2015, 33(17): 3660-3671.

[11] 李笑, 高毅, 吴昊, et al. 基于混合输入神经网络的φ-OTDR系统模式识别方法[J]. 中国激光, 2023, 50(11): 273-279.

    LI X, GAO Y, WU H. Mode recognition method of Ф-OTDR system based on mixed input neural network[J]. Chinese Journal of Lasers, 2023, 50(11): 273-279.

[12] LU Y, ZHU T, CHEN L, et al. Distributed vibration sensor based on coherent detection of Ф-OTDR[J]. Journal of Lightwave Technology, 2010, 28(22): 3243-3249.

[13] MARTINS H F, MARTIN-LOPEZ S, CORREDERA P, et al. Phase-sensitive optical time domain reflectometer assisted by first-order Raman amplification for distributed vibration sensing over >100 km[J]. Journal of Lightwave Technology, 2014, 32(8): 1510-1518.

[14] WANG Z N, ZENG J J, LI J, et al. Ultra-long phase-sensitive OTDR with hybrid distributed amplification[J]. Optics Letters, 2014, 39(20): 5866-5869.

[15] SHA Z, FENG H, SHI Y, et al. Phase-sensitive OTDR with 75-km single-end sensing distance based on RP-EDF amplification[J]. IEEE Photonics Technology Letters, 2017, 29(16): 1308-1311.

[16] FAN C Z, LI H, ZHANG K Y, et al. 300 km ultralong fiber optic DAS system based on optimally designed bidirectional EDFA relays[J]. Photonics Research, 2023, 11(6): 968-977.

[17] LIANG J J, WANG Z Y, LU B, et al. Distributed acoustic sensing for 2D and 3D acoustic source localization[J]. Optics Letters, 2019, 44(7): 1690-1693.

[18] SUN Y, LI H, FAN C, et al. Review of a specialty fiber for distributed acoustic sensing technology[J]. Photonics, 2022, 9(5): 277.

[19] LI J, ZHU W, BIONDI E, et al. Earthquake focal mechanisms with distributed acoustic sensing[J]. Nature Communications, 2023, 14(1): 4181.

[20] LIU S Q, SHAO L Y, YU F H, et al. Quantitative demodulation of distributed low-frequency vibration based on phase-shifted dual-pulse phase-sensitive OTDR with direct detection[J]. Optics Express, 2022, 30(6): 10096-10109.

[21] MASOUDI A, BELAL M, NEWSON T. A distributed optical fibre dynamic strain sensor based on Ф-OTDR[J]. Measurement Science and Technology, 2013, 24(8): 085204.

[22] FANG G, XU T, FENG S, et al. Phase-sensitive optical time domain reflectometer based on phase-generated carrier algorithm[J]. Journal of Lightwave Technology, 2015, 33(13): 2811-2816.

[23] WANG Z, ZHANG L, WANG S, et al. Coherent Ф-OTDR based on I/Q demodulation and homodyne detection[J]. Optics Express, 2016, 24(2): 853-858.

[24] YANG G, FAN X, WANG S, et al. Long-range distributed vibration sensing based on phase extraction from phase-sensitive OTDR[J]. IEEE Photonics Journal, 2016, 8(3): 1-2.

[25] KAMINOW I. Polarization in optical fibers[J]. IEEE Journal of Quantum Electronics, 1981, 17(1): 15-22.

[26] QIN Z, ZHU T, CHEN L, et al. High sensitivity distributed vibration sensor based on polarization-maintaining configurations of phase-OTDR[J]. IEEE Photonics Technology Letters, 2011, 23(15): 1091-3.

[27] LIU Y, WANG F, ZHANG X, et al. High perfmance interrogation by a compositedoubleprobepulse f ultraweak FBG array[C]SPIE, 2019, 11048: 731734.

[28] ZHANG Y, XU Y, SHAN Y, et al. Polarization dependence of phase-sensitive optical time-domain reflectometry and its suppression method based on orthogonal-state of polarization pulse pair[J]. Optical Engineering, 2016, 55(7): 074109.

[29] YU X, MENG Z. Polarization dependence of the noise of phase measurement based on phase-sensitive OTDR[J]. Journal of Optics, 2017, 19(12): 125602.

[30] YU Z, LU Y, MENG Z. Polarization dependence of Rayleigh interference signal in phasesensitive OTDR [C]2017 Conference on Lasers ElectroOptics Pacific Rim (CLEOPR), Singape, 2017: 13.

[31] WANG F, LIU Y, WEI T, et al. Polarization fading elimination for ultra-weak FBG array-based Φ-OTDR using a composite double probe pulse approach[J]. Optics Express, 2019, 27(15): 20468-20478.

[32] REN M, LU P, CHEN L, et al. Theoretical and experimental analysis of Φ-OTDR based on polarization diversity detection[J]. IEEE Photonics Technology Letters, 2016, 28(6): 697-700.

[33] LI H, LIU Y J, He T, et al. Dualpulse complex superposition based noise suppression f distributed acoustic sensing[C]2020 Conference on Lasers ElectroOptics (CLEO), San Jose, CA, USA, 2020: 12.

[34] LIU Y, LI H, LIU T, et al. Polarization dependent noise suppression f fiber distributed acoustic sens with birefringence estimation[C]2020 Conference on Lasers ElectroOptics (CLEO), San Jose, CA, USA, 2020:12.

[35] Chen D, Liu Q, He Z. Distributed fiberoptic acoustic sens with subnano strain resolution based on timegated digital OFDR[C]2017 Asia Communications Photonics Conference (ACP), Guangzhou, China, 2017: 13.

[36] REN M, LU P, CHEN L, et al. Theoretical and experimental analysis of Ф-OTDR based on polarization diversity detection[J]. IEEE Photonics Technology Letters, 2015, 28(6): 697-700.

[37] JUAREZ J C, TAYLOR H F. Polarization discrimination in a phase-sensitive optical time-domain reflectometer intrusion-sensor system[J]. Optics Letters, 2005, 30(24): 3284.

[38] GUERRIER S, DORIZE C, AWWAD E, et al. Introducing coherent MIMO sensing, a fading-resilient, polarization-independent approach to Φ-OTDR[J]. Optics Express, 2020, 28(14): 21081-21094.

[39] WANG Y, XIAO L, LI Y, et al. Polarization-fading suppression of Ф-OTDR with Rayleigh gray-scale pattern aggregation method[J]. Applied Optics, 2021, 60(33): 10429-10436.

[40] AN Y, FENG X, LI J, et al. Two-beam phase-sensitive optical time domain reflectometer based on Jones matrix modeling[J]. Optical Engineering, 2013, 52(9): 094102.

[41] LU L, SONG Y, ZHU F, et al. Coherent optical time domain reflectometry using three frequency multiplexing probe[J]. Opt Lasers Eng, 2012, 50(12): 1735-1739.

[42] ZHOU J, PAN Z Q, YE Q, et al. Characteristics and explanations of interference fading of a Ф-OTDR with a multi-frequency source[J]. Journal of Lightwave Technology, 2013, 31: 2947-2954.

[43] ZHOU J, PAN Z Q, YE Q, et al. Phase demodulation technology using a multi-frequency source for discrimination of interference-fading induced false alarms in a φ-OTDR system[J]. Chinese Journal of Lasers, 2013, 40(9): 905003.

[44] CHEN D, LIU Q W, HE Z Y. Phase-detection distributed fiber-optic vibration sensor without fading-noise based on time-gated digital OFDR[J]. Optics Express, 2017, 25(7): 8315-8325.

[45] HARTOG A H, LIOKUMOVICH L B, USHAKOV N A, et al. The use of multi‐frequency acquisition to significantly improve the quality of fibre‐optic‐distributed vibration sensing[J]. Geophys Prospect, 2018, 66(S1): 192-202.

[46] CHEN D, LIU Q W, HE Z Y. High-fidelity distributed fiber-optic acoustic sensor with fading noise suppressed and sub-meter spatial resolution[J]. Optics Express, 2018, 26(13): 16138.

[47] LIN S, WANG Z N, XIONG J, et al. Rayleigh fading suppression in one-dimensional optical scatters[J]. IEEE Access, 2019, 7: 17125-17132.

[48] ZABIHI M, CHEN Y, ZHOU T, et al. Continuous fading suppression method for Φ-OTDR systems using optimum tracking over multiple probe frequencies[J]. Journal of Lightwave Technology, 2019, 37(14): 3602-3610.

[49] ZHANG J, WU H, ZHENG H, et al. 80 km fading free phase-sensitive reflectometry based on multi-carrier NLFM pulse without distributed amplification[J]. Journal of Lightwave Technology, 2019, 37(18): 4748-4754.

[50] WU Y, WANG Z N, XIONG J, et al. Bipolar-coding Ф-OTDR with interference fading elimination and frequency drift compensation[J]. Journal of Lightwave Technology, 2020, 38(21): 6121-6128.

[51] GU J, LU B, YANG J, et al. High SNR Φ-OTDR based on frequency and wavelength diversity with differential vector aggregation method[J]. IEEE Photonics Journal, 2020, 12(6): 1-12.

[52] OGDEN H M, MURRAY M, MURRAY J, et al. Frequency multiplexed coherent Ф-OTDR[J]. Scientific Reports, 2021, 11(1): 17921.

[53] WAKISAKA Y, IIDA D, OSHIDA H, et al. Fading suppression of Φ-OTDR with the new signal processing methodology of complex vectors across time and frequency domains[J]. Journal of Lightwave Technology, 2021, 39(13): 4279-93.

[54] WAKISAKA Y, IIDA D, KOSHIKIYA Y, et al. Sampling rate enhancement and fading suppression of Φ-OTDR with frequency division multiplex technique[J]. Journal of Lightwave Technology, 2022, 40(3): 822-836.

[55] WANG Y, LI Y, XIAO L, et al. Interference fading suppression using active frequency transformation method with auxiliary interferometer feedback[J]. Journal of Lightwave Technology, 2022, 40(3): 872-879.

[56] LIN Z, HE H, ZHAO Z, et al. Frequency response enhanced quantitative vibration detection using fading-free coherent Φ-OTDR with randomized sampling[J]. Journal of Lightwave Technology, 2023, 41(15): 5159-5168.

[57] ZHANG H, ZHOU J, MA Y, et al. Fading suppression in the Ф-OTDR system based on a phase-modulated optical frequency comb[J]. Optics Express, 2023, 31(24): 40907-40915.

[58] 雷艳阳, 姜桃飞, 马云宾, et al. 基于宽带声光调制的高保真相位敏感光时域反射计系统[J]. 光学学报, 2024, 44(1): 231426.

    LEI Y Y, JIANG T F, MA Y B. High fidelity phase-sensitive optical time domain reflectometer system based on broadband acousto-optic modulation[J]. Acta Optica Sinica, 2024, 44(1): 231426.

[59] WANG Y, WANG J, FAN Y, et al. Interference fading suppression for distributed acoustic sensor using frequency-shifted delay loop[J]. Optics & Laser Technology, 2024, 171: 110441.

[60] WANG J, WANG Y, BAI Q, et al. Recognition suppression of phasesensitive OTDR interference fading based on machine learning[C]SPIE, 2024, 13498: 1349806.

[61] 谢浪, 吴明松, 王粤晖, et al. 多频COTDR系统的相位解调优化方法[J]. 光学学报, 2024, 44(1): 231442-340.

    XIE L, WU M S, WANG Y H. Phase demodulation optimization method for multi-frequency COTDR system[J]. Acta Optica Sinica, 2024, 44(1): 231442.

[62] LUO Y, LIU Q, LIU C, et al. A fading noise suppression method based on frequencyshift loop in TGDOFDR system[C]2024 Asia Communications Photonics Conference (ACP) International Conference on Infmation Photonics Optical Communications (IPOC), Beijing, China, 2024: 13.

[63] JIANG Y, GAO X, HE W, et al. Frequency multiplexed dual-pulse fiber-optic Φ-OTDR for a fading-free distributed fiber sound sensor[J]. Applied Optics, 2024, 63(19): 59-66.

[64] WU Y C, WEI Z H, LI T R, et al. Three-layer structure multiplexing fading elimination method in long-haulΦ-OTDR[J]. Journal of Lightwave Technology, 2024, 42(14): 5017-5024.

[65] LI J T, CHANG B, DU J T, et al. Coherently parallel fiber-optic distributed acoustic sensing using dual Kerr soliton microcombs[J]. Science Advances, 2024, 10(3): 1362.

[66] PAN Z, LIANG K, ZHOU J, et al. Interferencefadingfree phasedemodulated OTDR system[C]SPIE, 2012, 8421: 418421.

[67] WANG X, LU B, WANG Z, et al. Interference-fading-free Φ-OTDR based on differential phase shift pulsing technology[J]. IEEE Photonics Technology Letters, 2018, 31(1): 39-42.

[68] CUI K, LIU F, WANG K, et al. Interference-fading-suppressed pulse-coding Φ-OTDR using spectrum extraction and rotated-vector-sum method[J]. IEEE Photonics Journal, 2021, 13(6): 1-6.

[69] LIANG Y, WANG Z, LIN S, et al. Optical-pulse-coding phase-sensitive OTDR with mismatched filtering[J]. Science China Information Sciences, 2022, 65(9): 192303.

[70] LIANG C, LU Y, ZHANG X, et al. Fading noise reduction utilizing multiwavelength scheme in phase interrogation based phasesensitive optical time domain reflectometry [C]2018 Asia Communications Photonics Conference (ACP), Hangzhou, China, 2018:13.

[71] SAGUES M, PINEIRO E, CERRI E, et al. Two-wavelength phase-sensitive OTDR sensor using perfect periodic correlation codes for measurement range enhancement, noise reduction and fading compensation[J]. Optics Express, 2021, 29: 6021-6035.

[72] LI H, LIU T, FAN C, et al. Fading suppression for distributed acoustic sensing assisted with dual-laser system and differential-vector-sum algorithm[J]. IEEE Sensors Journal, 2022, 22(10): 9417-9425.

[73] ALEKSEEV A E, VDOVENKO V S, GORSHKOV B G, et al. Fading reduction in a phase optical time-domain reflectometer with multimode sensitive fiber[J]. Laser Physics, 2016, 26(9): 095101.

[74] SUTI D, MARCON G, TUROLLA A, et al. Analysis of distributed acoustic sensing in multimode fibers based on heterodyne optical time domain reflectometry[C]In 27th International Conference on Optical Fiber Senss, Technical Digest Series (Optica Publishing Group, 2022.

[75] ORSUTI D, MARCON G, TUROLLA A, et al. DAS over multimode fibers with reduced fading by coherent averaging of spatial modes[J]. IEEE Photonics Technology Letters, 2023, 35(16): 866-869.

[76] CHEN M, MASOUDI A, PARMIGIANI F, et al. Distributed acoustic sensor based on a two-mode fiber[J]. Optics Express, 2018, 26(19): 25399-25407.

[77] ZHAO Z, WU H, HU J, et al. Interference fading suppression in Ф-OTDR using space-division multiplexed probes[J]. Optics Express, 2021, 29(10): 15452-15462.

[78] LIU Y, YANG J, WU B, et al. High SNR Φ-OTDR with multi-transverse modes heterodyne matched-filtering technology[J]. Sensors, 2021, 21(22): 7460.

[79] LU B, GU J, WANG Z, et al. Ultra-low-noise MIMO distributed acoustic sensor using few-mode optical fibers[J]. Journal of Lightwave Technology, 2022, 40(9): 3062-3071.

[80] ZHANG Y X, LIU J X, XIONG F, et al. A space-division multiplexing method for fading noise suppression in the Φ-OTDR system[J]. Sensors, 2021, 21(5): 1694.

[81] LIUY, LIU H, XIAO Y, et al. False alarms mitigation in ΦOTDR system using multice fiber with crelation algithms[C]2023 IEEE 8th Optoelectronics Global Conference (OGC), Shenzhen, China, 2023: 8185.

[82] XIAO Y H, LIU H H, ZHAO Z Y, et al. Fading suppression enhanced signaltonoise ratio in multice fiber integrated ФOTDR system[C]2023 IEEE 8th Optoelectronics Global Conference (OGC), Shenzhen, China, 2023: 7275.

[83] LIU T, WANG F, ZHANG X, et al. Interrogation of ultra-weak FBG array using double-pulse and heterodyne detection[J]. IEEE Photonics Technology Letters, 2018, 30(8): 677-680.

[84] WU M, FAN X, LIU Q, et al. Highly sensitive quasi-distributed fiber-optic acoustic sensing system by interrogating a weak reflector array[J]. Optics Letters, 2018, 43(15): 3594-3597.

[85] LI H, SUN Q, LIU T, et al. Ultra-high sensitive quasi-distributed acoustic sensor based on coherent OTDR and cylindrical transducer[J]. Journal of Lightwave Technology, 2019, 38(4): 929-938.

[86] REDDING B, MURRAY M J, DONKO A, et al. Low-noise distributed acoustic sensing using enhanced backscattering fiber with ultra-low-loss point reflectors[J]. Optics Express, 2020, 28(10): 14638-14647.

[87] HONG R, ZHANG Z, WANG F, et al. Enhancing the performance of DAS using a dual-wavelength UWFBG array with alternating arrangement[J]. Optics & Laser Technology, 2025, 181: 111864.

[88] WANG Z, YANG J, GU J, et al. Practical performance enhancement of DAS by using dense multichannel signal integration[J]. Journal of Lightwave Technology, 2021, 39(19): 6348-6354.

[89] SAMI M, HOCINE M, LOTFY MOKHTAR S. Noise and fading reduction in a phase-OTDR system using a multi-strand optical fiber sensing cable[J]. Applied Optics, 2024, 63(18): 4883-4890.

[90] PANG F, HE M, LIU H, et al. A fading-discrimination method for distributed vibration sensor using coherent detection of Ф-OTDR[J]. IEEE Photonics Technology Letters, 2016, 28(23): 2752-2755.

[91] WU Y, WANG Z, XIONG J, et al. Interference fading elimination with single rectangular pulse in Ф-OTDR[J]. Journal of Lightwave Technology, 2019, 37(13): 3381-3387.

[92] TU G, ZHAO M, TANG Z, et al. Fading noise suppression in Φ-OTDR based on nearest neighbor analysis[J]. Journal of Lightwave Technology, 2020, 38(23): 6691-6698.

[93] HE X, XU X, ZHANG M, et al. On the phase fading effect in the dual-pulse heterodyne demodulated distributed acoustic sensing system[J]. Optics Express, 2020, 28(22): 33433-33447.

[94] ZHANG X, WANG Q, XIONG F, et al. Performance enhancement method for phase-sensitive optical time-domain reflectometer system based on suppression of fading induced false alarms[J]. Optical Engineering, 2020, 59(4): 046101.

[95] MA Z, JIANG J F, LIU K, et al. Virtual-block-array phase analysis for distributed acoustic sensors with a high signalto-noise ratio reconstruction waveform[J]. Optics Express, 2020, 28(17): 24577-24585.

[96] ZHANG Y, ZHOU T, DING Z, et al. Classification of interference-fading tolerant Φ-OTDR signal using optimal peak-seeking and machine learning[J]. Chinese Optics Letters, 2021, 19(3): 030601.

[97] ZHANG X, ZHENG Y, ZHANG C, et al. A fading tolerant phase-sensitive optical time domain reflectometry based on phasing-locking structure[J]. Electronics, 2021, 10(5): 535.

[98] HE H, YAN L, QIAN H, et al. Suppression of the interference fading in phase-sensitive OTDR with phase-shift transform[J]. Journal of Lightwave Technology, 2020, 39(1): 295-302.

[99] QIAN H, LUO B, HE H, et al. Fading-free Φ-OTDR with multi-frequency decomposition[J]. IEEE Sensors Journal, 2021, 22(3): 2160-2166.

[100] LI H, FAN C, SHI Z, et al. Spatio-temporal joint oversampling-downsampling technique for ultra-high resolution fiber optic distributed acoustic sensing[J]. Optics Express, 2022, 30(16): 29639-29654.

[101] QIAN H, LUO B, HE H, et al. Fading-free Φ-OTDR evaluation based on the statistical analysis of phase hopping[J]. Applied Optics, 2022, 61(23): 6729-9735.

[102] QU S, WANG M, DING S, et al. Coherent fading suppression of distributed acoustic sensing based on time-frequency domain linkage algorithm[J]. Measurement Science and Technology, 2024, 35(12): 125114.

[103] LI T X, ZHANG F D, LIN J, et al. Fading noise suppression method of Φ-OTDR system based on GA-VMD algorithm[J]. IEEE Sensors Journal, 2023, 23(19): 22608-22619.

[104] LI T, ZHANG F, LIN J, et al. Fading noise suppression method of Ф-OTDR system based on non-local means filtering[J]. Optical Fiber Technology, 2023, 81: 103572.

[105] SUN M, YU M, WANG H, et al. Fading discrimination and suppression of DAS system based on FAM-MAE[J]. IEEE Sensors Journal, 2023, 23(24): 30463-30472.

[106] YU F, LIU S, XU D, et al. Integrated fading suppression for phase-sensitive OTDR: an algorithm set[J]. Journal of Lightwave Technology, 2024, 42(5): 1754-1764.

[107] XU D, YU F, LIU S, et al. Suppression of the interference fading in heterodyne Φ-OTDR with fast signal synthesis algorithm[J]. Measurement Science and Technology, 2024, 36(1): 015108.

[108] WANG Y, HE C, DU W, et al. Interference fading suppression with fault-tolerant Kalman filter in phase-sensitive OTDR[J]. ISA Transactions, 2024, 150: 298-310.

[109] HU T, YANG S T, YUAN L B. Vectorial distributed vibration sensing based on two-beam Ф-OTDR and four-core fiber[J]. Journal of Lightwave Technology, 2024, 42(13): 4674-4680.

[110] CHENG Z, SHI Y. High quality phase demodulation method for direct detection Φ-OTDR[J]. Optics Express, 2024, 32(4): 6630-6643.

雷艳阳, 陈金博, 刘帅旗, 李天夫, 董永康. Ф-OTDR系统中的衰落效应抑制研究进展(特邀)[J]. 红外与激光工程, 2025, 54(4): 20250051. Yanyang LEI, Jinbo CHEN, Shuaiqi LIU, Tianfu LI, Yongkang DONG. Research progress of fading effect suppression in Ф-OTDR system (invited)[J]. Infrared and Laser Engineering, 2025, 54(4): 20250051.

点击上图查看本文图集
论文摘要 Full Text  图 & 表 补充材料 基本信息 知识挖掘 Metrics PDF全文参考文献 & 引文
引用该论文： TXT   |   EndNote

被引通知
PDF全文

相关论文

加载中...

相关资讯

加载中...

关于本站 Cookie 的使用提示

中国光学期刊网使用基于 cookie 的技术来更好地为您提供各项服务，点击此处了解我们的隐私策略。 如您需继续使用本网站，请您授权我们使用本地 cookie 来保存部分信息。
全站搜索
您最值得信赖的光电行业旗舰网络服务平台!
快速查询 高级查询
最近搜索：
大家在搜： 人工智能     图像处理     光子 
热门搜索： 机器视觉     光通信     光纤传感器