基于BAS-PSO算法的机器人定位精度提升

乔贵方; 吕仲艳; 张颖; 宋光明; 宋爱国

doi:doi:10.37188/OPE.20212904.0763

光学精密工程, 2021, 29 (4): 763, 网络出版: 2021-10-13

基于BAS-PSO算法的机器人定位精度提升下载： 807次

Improvement of robot kinematic accuracy based on BAS-PSO algorithm

论文大纲

乔贵方 ^1,2,*吕仲艳 ¹张颖 ¹宋光明 ²宋爱国 ²

作者单位

¹ 南京工程学院自动化学院，江苏南京267

² 东南大学仪器科学与工程学院，江苏南京10096

摘要

鉴于工业机器人的精度性能无法满足高端制造领域的要求，研究了机器人定位精度提升方法，阐述了基于位姿微分变换的运动学误差模型和基于坐标误差传递的运动学误差模型的构建方法，提出了一种基于BAS-PSO算法的运动学参数辨识方法，并通过实验对比分析了不同运动学误差模型的精度。实验结果表明，基于BAS-PSO算法辨识后TX60机器人的平均综合位置/姿态误差分别从（0.312 mm，0.221°）降低为（0.093 8 mm，0.044 2°）；而基于正运动学模型直接辨识后机器人的平均位置误差和平均姿态误差分别为0.097 5 mm和0.098 6°。本文提出的BAS-PSO算法具有较好的辨识精度和收敛速度，直接利用正运动学模型辨识的机器人运动学参数具有更好的辨识稳定性和精度。

Abstract

In this study， a method to improve robot positioning accuracy was proposed， given that the accuracy performance of industrial robots still does not satisfy the requirements of high-end manufacturing. First， a kinematics error model based on pose differential transformation and kinematics error model based on coordinate error transformation were summarized. Second， a kinematic parameters identification method based on BAS-PSO algorithm was proposed. Finally， accuracy characteristics of different error models were compared and analyzed via experiments. The experimental results indicate that the average comprehensive position/attitude error of the TX60 robot， after identification by the proposed algorithm， decreases from （0.312 mm， 0.221°） to （0.093 8 mm， 0.044 2°）. The average position error and average attitude error of the robot after direct identification based on the forward kinematics model correspond to 0.097 5 mm and 0.098 6°， respectively. The BAS-PSO algorithm proposed in the study displays good performance in terms of identification accuracy and convergence speed. Furthermore， robot kinematic parameters directly identified by the forward kinematics model exhibit better identification stability and accuracy.

1 引　言

近年来，工业机器人逐渐被应用于航天发动机的叶片智能磨抛、航天工业中钻铆/装配以及制造现场在线测量系统等高端制造领域^［1-3］。“智能机器人”重点专项指出工业机器人应用于高端制造领域时，其绝对定位精度应优于±0.1 mm，姿态角精度应优于±0.1°。目前，工业机器人的重复定位精度最高能够达到0.01 mm，而绝对定位精度仍为毫米级，无法满足高端制造领域的精度要求。

机器人标定技术常被用于提高工业机器人的绝对定位精度^［4-5］。机器人定位误差的诱因较多，其中运动学参数误差是影响机器人定位精度的主要误差源之一^［6-7］。目前，机器人标定方法主要包含误差模型法和轴线测量法，相比于轴线测量法，误差模型法的标定精度更高^［8］。基于误差模型法的机器人标定过程主要有误差建模、误差测量、参数辨识及误差补偿4个基本步骤。运动学模型对误差模型的建模影响较大，当前机器人控制器中广泛使用的运动学模型有DH模型，M-DH模型，POE模型和ZRM模型等。误差模型的完整性决定了运动学模型参数的辨识精度。根据测量数据的不同，误差模型主要分为位姿误差模型、位置误差模型和距离误差模型，其中位姿误差模型完整描述了机器人的位置误差和姿态误差特性^［9］；从建模方法主要分为微分变换^［10］和误差传递两种^［11］，两者在建模过程中忽略的高阶误差项不同，目前尚未有针对两者精度性能对比的相关研究。

误差测量主要采用激光跟踪仪、测量臂、拉线传感器和多目视觉测量系统等。其中，激光跟踪仪因其高精度、测量范围大等特点，是最为常用的测量设备^［12-13］。参数辨识是非线性函数求解问题，主要采用Levenberg-Marquardt法、极大似然法^［14］等传统优化算法，但算法的收敛速度和精度依赖于目标函数的雅克比矩阵的奇异值。而智能优化算法则不存在此类问题，LIU等人利用遗传算法实现六自由度串联机器人的运动学参数标定^［15］。房立金等人基于量子粒子群算法分别实现了串联/并联机器人的运动学参数标定^［16］。温秀兰等人利用改进乌鸦算法辨识机器人的运动学参数，将史陶比尔TX60机器人的位姿精度提升了70%^［17］。

本文针对六自由度串联机器人定位精度的提升方法展开研究，提出了一种基于天牛须搜索和粒子群优化（Beetle Antennea Search-Particle Swarm Optimization，BAS-PSO）算法的运动学参数辨识方法，并通过实验验证了不同误差模型构建方法的辨识精度和稳定性。

2 机器人运动学误差模型建立

2.1　建立M-DH运动学模型

如图1（a）所示，传统的DH模型利用连杆长度a、连杆距离d、连杆扭角α和关节零位θ 4个参数描述了机器人连杆间的位姿关系。而M-DH解决了传统DH模型在机器人相邻两轴平行或接近平行时的奇异性问题，该模型在传统DH模型基础上添加了一个角度参数β来描述相邻平行轴的位置关系^［18］，如图1（b）所示。依据M-DH模型的建立规则，机器人连杆相邻坐标系之间的变换关系为：

\begin{matrix} A_{i}^{n} = R o t (Z_{i}, θ_{i}) T r a n s (Z_{i}, d_{i}) T r a n s (X_{i}, a_{i}) R o t (X_{i}, α_{i}) R o t (Y_{i}, β_{i}) = \\ [\begin{matrix} - s i n θ_{i} s i n α_{i} s i n β_{i} + c o s θ_{i} c o s β_{i} & - s i n θ_{i} c o s α_{i} & s i n θ_{i} s i n α_{i} c o s β_{i} + c o s θ_{i} s i n β_{i} & a_{i} c o s θ_{i} \\ c o s θ_{i} s i n α_{i} s i n β_{i} + s i n θ_{i} c o s β_{i} & c o s θ_{i} c o s α_{i} & - c o s_{i} s i n α_{i} c o s β_{i} + s i n θ_{i} s i n β_{i} & a_{i} s i n θ_{i} \\ - c o s α_{i} s i n β_{i} & s i n α_{i} & c o s α_{i} c o s β_{i} & d_{i} \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix}

式中：a_i，d_i，α_i，θ_i，β_i分别表示机器人第i个关节的连杆长度、连杆距离、连杆扭角、关节零位及关节扭角，i=1，2，…，6。n表示该转换矩阵带入名义运动学模型参数。

图 1. 非平行关节(a)与平行关节(b)的坐标系转换

Fig. 1. Coordinate transformation between non-parallel joints (a) and parallel joints (b)

下载图片查看所有图片

因此，机器人的名义末端位姿可由矩阵T_n求取：

T_{n} = A_{1}^{n} A_{2}^{n} A_{3}^{n} A_{4}^{n} A_{5}^{n} A_{6}^{n} = [\begin{matrix} R_{n} & P_{n} \\ 0 & 1 \end{matrix}]

式中：R_n和P_n分别为名义旋转矩阵和名义位移向量。

本文待标定的工业机器人Staubli TX60的 M-DH模型参数的名义值如表1所示。由于关节2与关节3理论上是平行关系，则运动学模型参数d₂=0，β₂=0。其余关节的β_i参数均为0，则式（1）变化为传统DH模型。

表 1. Staubli TX60机器人M-DH运动学模型的名义参数

Table 1. Nominal parameters of M-DH kinematics model of Staubli TX60 robot

i	θ_i/rad	d_i/mm	a_i/mm	α_i/rad
1	π	0	0	π/2
2	π/2	0	290	0
3	π/2	20	0	π/2
4	π	310	0	π/2
5	π	0	0	π/2
6	0	70	0	0

查看所有表

而实际情况中机器人的运动学模型参数a_i，d_i，α_i，θ_i，β_i存在一定误差Δa_i，Δd_i，Δα_i，Δθ_i，Δβ_i，因此，机器人实际末端位姿可由矩阵T_r计算：

T_{r} = A_{1}^{r} A_{2}^{r} A_{3}^{r} A_{4}^{r} A_{5}^{r} A_{6}^{r} = [\begin{matrix} R_{r} & P_{r} \\ 0 & 1 \end{matrix}]

式中：R_r和P_r分别为实际的旋转矩阵和位移向量。r表示该转换矩阵带入的实际运动学模型参数。

建立机器人运动学误差模型是机器人标定技术的关键步骤之一，误差模型决定了运动学参数的辨识精度。误差模型类型主要有位姿误差模型、位置误差模型和距离误差模型，其中位姿误差模型能够较为完整地描述机器人的误差特性。建模方法主要分为微分变换和误差传递两种，本文通过实验验证了两种不同运动学误差模型用于标定的实际效果。

2.2　基于位姿微分变换的运动学误差模型

机器人末端的位姿误差矩阵dT表示为：

d T = T_{r} - T_{n}

对T_n每一列的运动学参数进行微分，并忽略高阶项（即2阶及以上），可以得到机器人的位姿误差模型：

Δ E = [\begin{matrix} P_{r} - P_{n} \\ n_{r} - n_{n} \\ o_{r} - o_{n} \\ a_{r} - a_{n} \end{matrix}] = [\begin{matrix} H_{p} \\ H_{n} \\ H_{o} \\ H_{a} \end{matrix}] Δ η = H Δ η

式中： $H = [\begin{matrix} \begin{matrix} \frac{\partial \cdot}{\partial θ} & \frac{\partial \cdot}{\partial d} \end{matrix} & \frac{\partial \cdot}{\partial a} & \frac{\partial \cdot}{\partial α} & \frac{\partial \cdot}{\partial β} \end{matrix}]$ ，为运动学参数的雅克比矩阵；Δη=［Δθ　Δd　Δa　Δα　Δβ］^Ｔ，为运动学参数的误差向量。

2.3　基于坐标误差传递的运动学误差模型

由于各运动学参数存在误差，相邻连杆坐标系间的转换矩阵存在误差，即：

A_{i}^{r} = A_{i}^{n} + d A_{i}

对A_iⁿ矩阵进行全微分，并忽略高阶项，可得：

\begin{matrix} d A_{i}^{n} = \frac{\partial A_{i}^{n}}{\partial θ_{i}} Δ θ_{i} + \frac{\partial A_{i}^{n}}{\partial d_{i}} Δ d_{i} + \frac{\partial A_{i}^{n}}{\partial a_{i}} Δ a_{i} + \\ \frac{\partial A_{i}^{n}}{\partial α_{i}} Δ α_{i} + \frac{\partial A_{i}^{n}}{\partial β_{i}} Δ β_{i} = δ A_{i}^{n} A_{i}^{n} \end{matrix}

式中：δA_iⁿ为连杆坐标系i-1下的微分变换矩阵，其表达式如下：

δ A_{i}^{n} = (\begin{matrix} 0 & - δ_{z i} & δ_{y i} & d_{x i} \\ δ_{z i} & 0 & - δ_{x i} & d_{y i} \\ - δ_{y i} & δ_{x i} & 0 & d_{z i} \\ 0 & 0 & 0 & 1 \end{matrix})

式中：d_i=（d_xi，d_yi，d_zi）^T，代表连杆i的一阶微分平移向量；δ_i=（δ_xi，δ_yi，δ_zi）^T，代表连杆i的实际姿态与名义姿态间的误差。

式（7）中给出了连杆i的误差在连杆i-1坐标系下的位姿误差和微分变化，因此，相对于机器人基坐标系的末端位姿可以表示为：

T_{r} = T_{n} + d T = \prod_{i = 1}^{6} (A_{i}^{n} + d A_{i}^{n})

当仅考虑一阶模型，忽略高阶项后，可得：

d T = δ T \cdot T^{n} = \sum_{i = 1}^{6} A_{i - 1}^{n} δ A_{i}^{n} (A_{i - 1}^{n})^{- 1} T^{n}

将各连杆相对于前一连杆的微分运动均转换为相对机器人基坐标系的微分运动，可得：

[\begin{matrix} d_{Δ} \\ δ_{Δ} \end{matrix}] = \sum_{i = 1}^{6} [\begin{matrix} R_{i - 1}^{N} & P_{i - 1}^{N} \times R_{i - 1}^{N} \\ 0 & R_{i - 1}^{N} \end{matrix}] [\begin{matrix} d_{i} \\ δ_{i} \end{matrix}]

式中：d_∆=（d_x_∆，d_y_∆，d_z_∆）^T，代表机器人末端的一阶微分平移向量；δ_∆=（δ_x∆，δ_y∆，δ_z∆）^T，代表机器人末端实际姿态与名义姿态的误差。

3 基于BAS-PSO的运动学参数辨识

3.1　BAS-PSO混合优化算法

天牛须搜索算法（Beetle Antennae Search，BAS）是2017年提出的一种新型智能优化算法，具有求解速度快、精度高、运算量少等特点^［19］。BAS是模拟天牛觅食原理，天牛的两只触角感知食物气味的强弱实现觅食，若左边触角感知的气味强度比右边大，天牛就往左飞；否则就往右飞，具体示意图如图2所示。BAS算法与其他智能优化算法类似，无需梯度信息就可以实现高效寻优。并且BAS算法中仅需一个个体，运算量大为降低，但容易陷入局部最优。

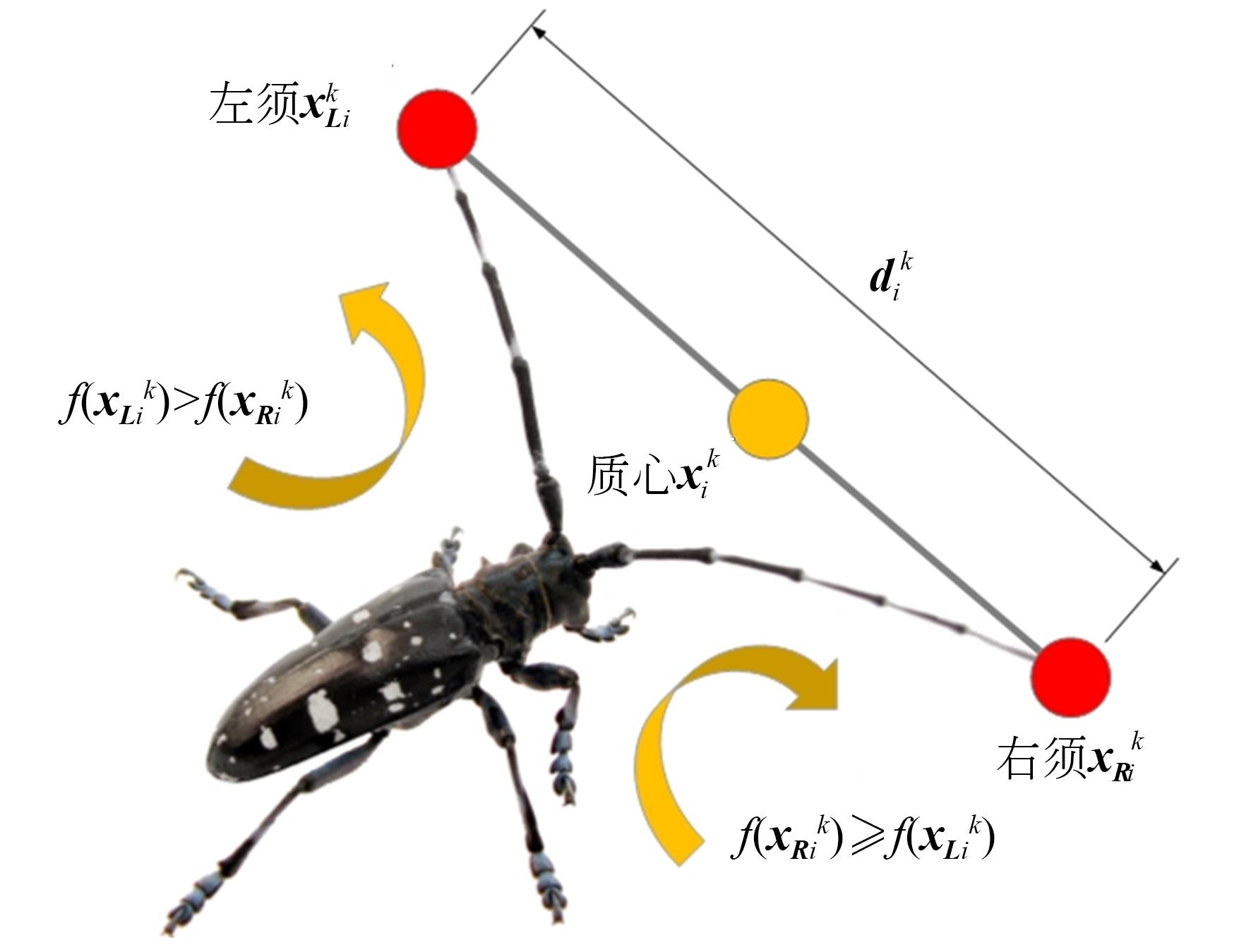
图 2. 天牛须搜索算法的仿生原理示意图

Fig. 2. Schematic diagram of bionic principle for beetle antennae search algorithm

下载图片查看所有图片

群体智能算法具有并行运算特性，通过多个个体的相互协作实现寻优，不易陷入局部最优。粒子群优化算法（Particle Swarm Optimization，PSO）是一种经典的群体智能算法，通过群体中粒子个体之间的协作和信息共享来寻找最优解，粒子个体通过跟踪个体极值和全局极值来更新位置。为提高粒子个体的多样性，同时提高BAS算法的并行性，本文提出一种BAS-PSO混合优化算法来实现机器人运动学参数的误差辨识。

BAS-PSO混合优化算法求解最优问题时，粒子个体的位置更新有两种途径：一是根据天牛须搜索算法更新当前位置；二是根据个体的最优值和个体群的全局最优值决定其更新位置。因此，第i个个体在k+1时刻的位置更新如下：

\{\begin{array}{l} v_{i}^{k + 1} = K [v_{i}^{k} + c_{1} r_{1} (x_{b} - x_{i}^{k}) + c_{2} r_{2} (x_{g} - x_{i}^{k}) + c_{3} B_{i}^{k + 1}] \\ x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k + 1} \end{array}

式中： $v_{i}^{k + 1}$ 是k+1次迭代的第i个个体速度， $x_{i}^{k + 1}$ 是k+1次迭代的第i个个体位置， $B_{i}^{k + 1}$ 是k+1次迭代的第i个天牛个体速度，x_b是个体最优位置，x_g是个体全体最优位置，r₁，r₂均是［0，1］之间的随机数，c₁，c₂，c₃均为固定的学习因子，K为收缩因子， $K = \frac{2}{\sqrt[]{2 - C - \sqrt[]{C^{2} - 4 C}}}$ ，其中C=c₁+c₂。

天牛个体的速度主要由左/右须位置的函数值决定，为保证该项在精度和全局收敛速度之间的平衡，通过变步长实现粗略搜索后再精细化搜索。因此，天牛个体的速度更新依据如下：

\{\begin{array}{l} B_{i}^{k + 1} = δ_{i}^{k + 1} \frac{r_{3}}{‖r_{3}‖} s i g n [f (x_{i}^{k} + d_{i}^{k + 1} \frac{r_{3}}{‖r_{3}‖}) - f (x_{i}^{k} - d_{i}^{k + 1} \frac{r_{3}}{‖r_{3}‖})] \\ d_{i}^{k + 1} = 0.95 d_{i}^{k} + d_{0} \\ δ_{i}^{k + 1} = 0.95 δ_{i}^{k} + δ_{0} \end{array}

式中：r₃是［0，1］之间的随机数， $d_{i}^{k + 1}$ 为天牛个体的须宽， $δ_{i}^{k + 1}$ 为天牛个体的运动步长，d₀与δ₀分别确定了最小须宽和最小步长。

通常个体的初始位置是通过伪随机数随机产生的，但其随机性过强而均匀性不足。根据文献［20］可知，拟随机序列相比于伪随机序列能够更加均匀地充满采样空间，可以提升优化算法的收敛速度，使计算结果更加稳定可靠。鉴于拟随机Halton序列概念清晰，算法易实现，用于产生BAS-PSO的初始位置。

3.2　误差模型的适应度函数

在采用BAS-PSO优化计算机器人的几何参数误差时，其适应度函数为：

f = m i n (\sum_{j = 1}^{N} \sqrt[]{k (n \cdot n + o \cdot o + a \cdot a) + p \cdot p})

（14）

式中：N为标定点数目，k为调节因子。由于位置误差和姿态误差的量纲不同，并且误差值相差较大，利用调节因子k平衡位置误差向量和姿态误差向量在目标函数中的权重。

由式（14）可知：f是几何参数误差集（Δa_i，Δd_i，Δα_i，Δθ_i，Δβ_i）的函数，经优化算法搜索机器人的几何参数误差集（Δa_i，Δd_i，Δα_i，Δθ_i，Δβ_i），使适应度函数f最小。本文中待标定的Staubli TX60六自由度串联机器人2，3关节的轴线理论上是平行的。因此，参数d₂，β₁，β₃，β₄，β₅，β₆不需要辨识，因此待辨识参数的个数为24，属于复杂的多参数非线性优化问题，非常适合采用智能优化算法求解。

4 运动学参数辨识实验

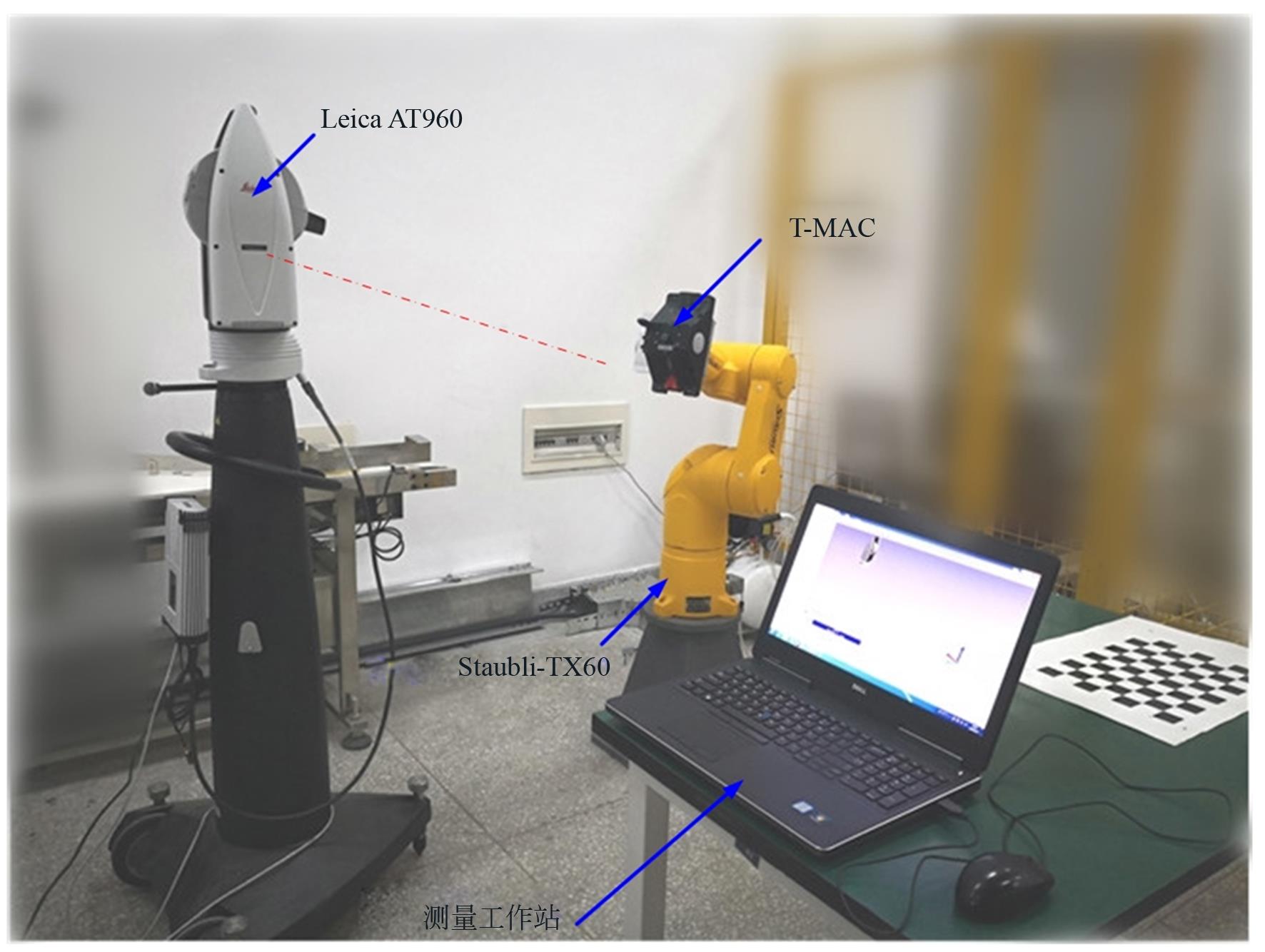
图3为本文所搭建的机器人标定实验系统，该系统使用Leica AT960激光跟踪仪，其测量不确定度为±（15 μm+6 μm/m）。配套使用的测量分析软件为Spatial Analyzer，该软件提供了拟合几何体、建立坐标系等功能。该系统待标定的工业机器人为Staubli TX60，该机器人的重复定位精度为±0.02 mm，额定负载为3 kg，最大负载为5 kg。激光跟踪仪的T-MAC工具安装在工业机器人的末端法兰盘上。本文所涉及的测量过程均符合GB/T-12642-2013及ISO-9283工业机器人性能规范及其试验方法标准。

图 3. 工业机器人标定系统

Fig. 3. Photo of industrial robot calibration system

下载图片查看所有图片

实验中以Staubli TX60机器人的基坐标系为参考坐标系，以坐标值（550，0，550）为中心点，在边长为1 000 mm的正方体空间内随机选择50个测量点用于运动学模型参数标定，并使这50个测量点要尽可能地分布在整个正方体空间内，同时在相同空间内选择30个验证点来验证运动学模型精度。

4.1　基于BAS-PSO的运动学参数辨识

本文首先基于位姿微分变换构建的运动学误差模型，利用BAS-PSO算法辨识机器人运动学模型参数，并与PSO算法和BAS算法进行对比。算法优化过程如图4所示，从图中可以看出，BAS-PSO算法的收敛速度比PSO算法和BAS算法快，并且适应度函数的值也比PSO算法的小。

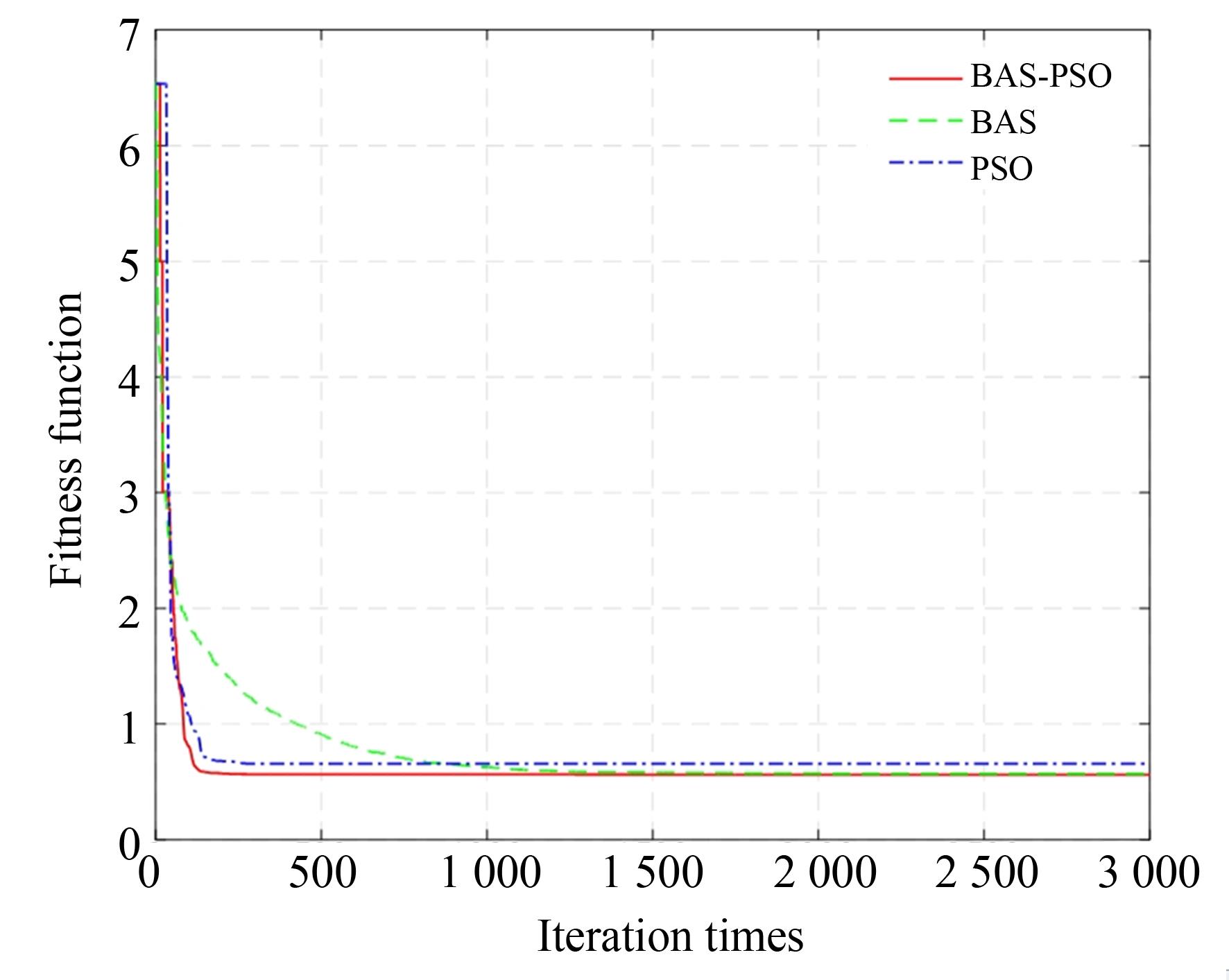
图 4. 不同优化算法的计算过程对比

Fig. 4. Calculation process comparison of different optimization algorithms

下载图片查看所有图片

机器人运动学模型参数的辨识精度如图5和图6所示。平均综合位置误差（Average Compre- hensive Position Error，ACPE）和平均综合姿态误差（Average Comprehensive Attitude Error，ACAE）的计算如下：

\{\begin{array}{l} R_{A C P E} = \frac{1}{M} \sum_{j = 1}^{M} \sqrt[]{(Δ x^{2} + Δ y^{2} + Δ z^{2})} \\ R_{A C A E} = \frac{1}{M} \sum_{j = 1}^{M} \sqrt[]{(Δ α^{2} + Δ β^{2} + Δ γ^{2})} \end{array}

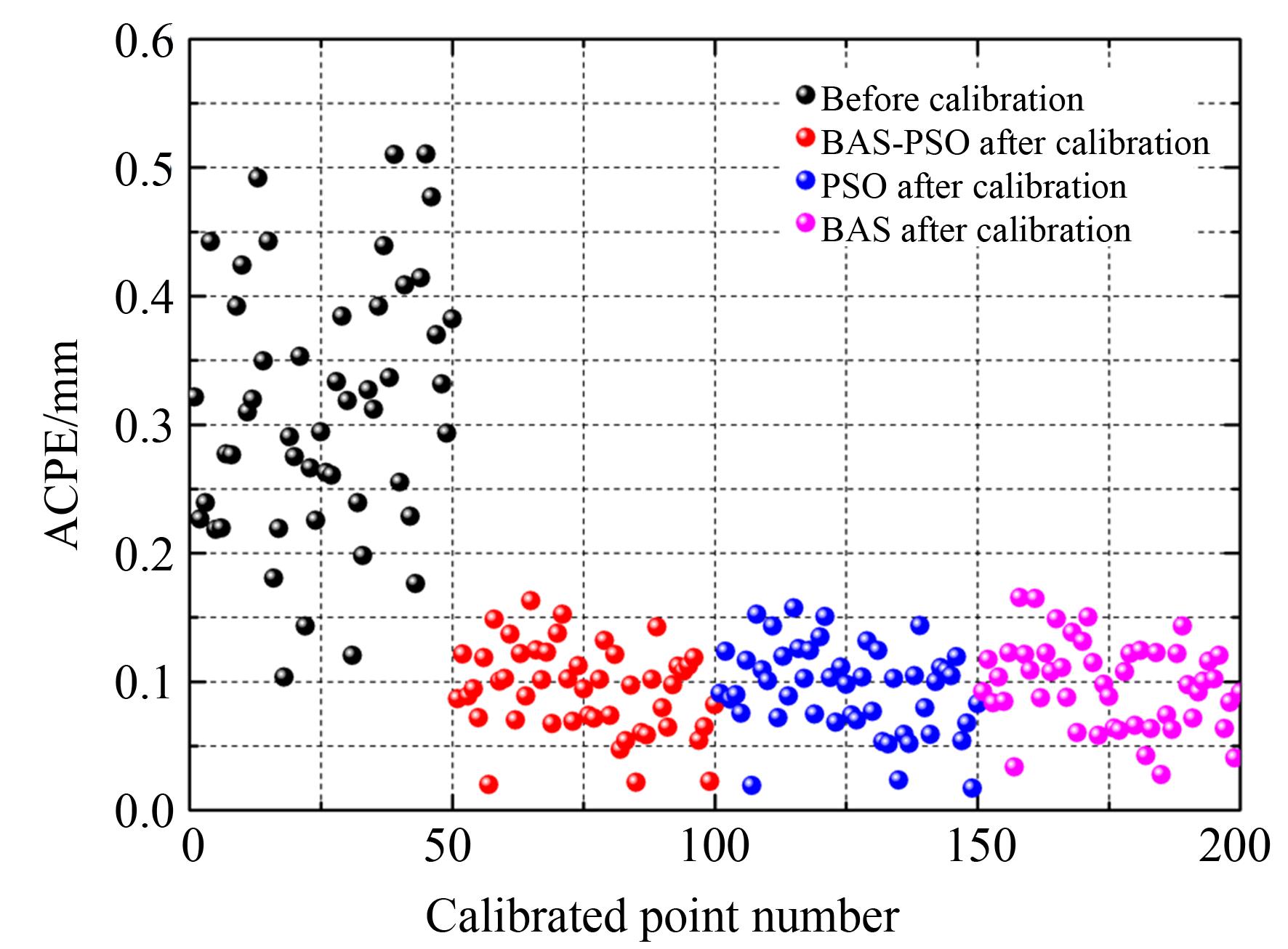
图 5. 标定前后机器人的平均综合位置误差

Fig. 5. Average comprehensive position errors（ACPE） of robot before and after calibration

下载图片查看所有图片

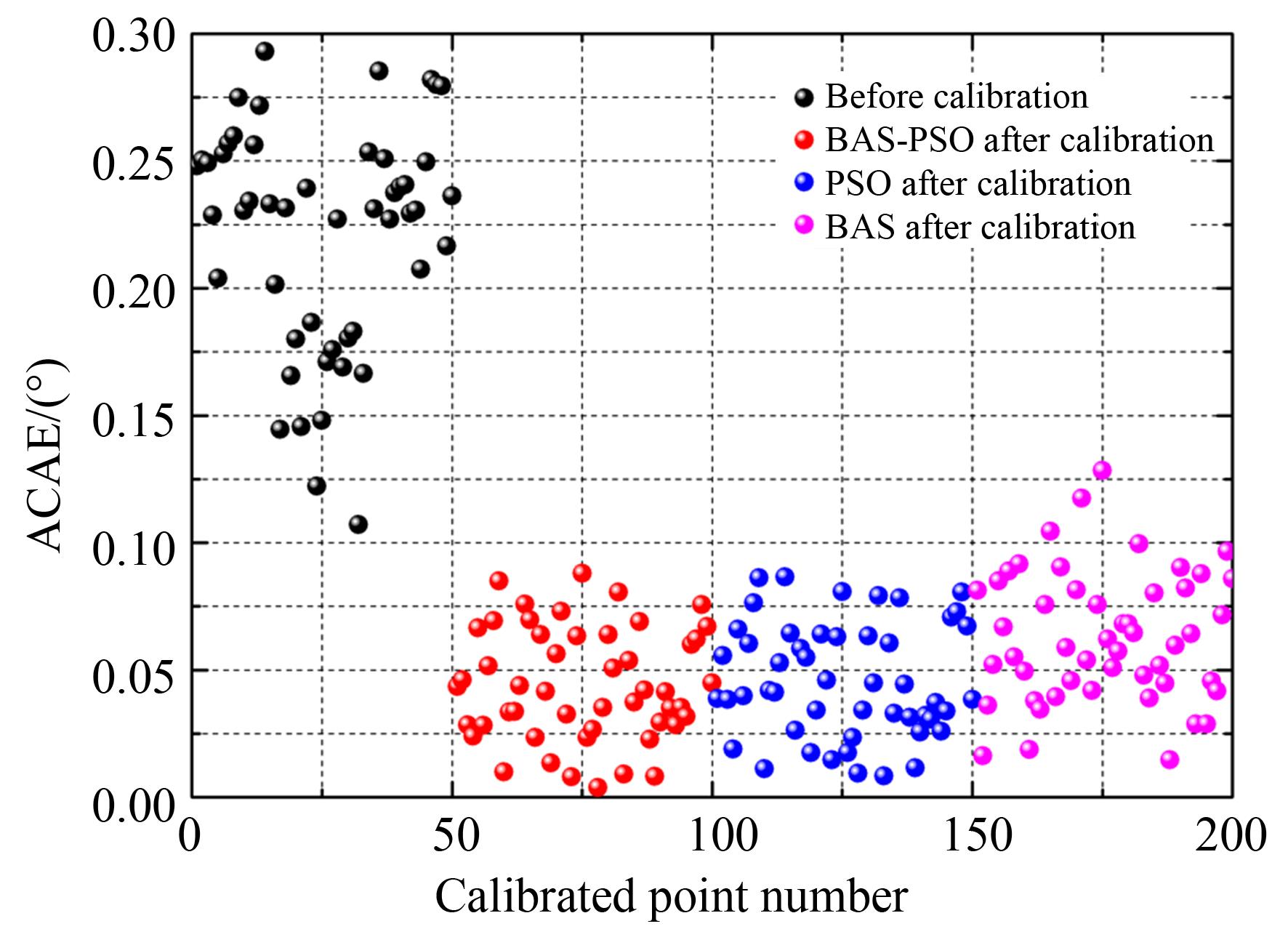
图 6. 标定前后机器人的平均综合姿态误差

Fig. 6. Average comprehensive attitude error（ACAE） of robot before and after calibration

下载图片查看所有图片

利用BAS-PSO算法辨识机器人的运动学参数误差，TX60机器人的ACPE，ACAE分别从（0.312 mm，0.221°）降低为（0.093 8 mm，0.044 2°）。而经过PSO算法和BAS算法辨识后的TX60机器人的ACPE，ACAE分别为（0.094 2 mm，0.045 9°）和（0.097 7 mm，0.063 2°）。从以上结果可以看出，BAS-PSO算法辨识得到的运动学参数误差具有更好的精度特性。为进一步验证辨识模型精度，本文分别计算30个验证点的ACPE和ACAE。利用BAS-PSO算法辨识后的机器人的ACPE，ACAE分别从（0.301 mm，0.233°）降低为（0.111 mm，0.047°）。而经过PSO算法和BAS算法辨识后的TX60机器人的ACPE，ACAE分别为（0.113 mm，0.051°）和（0.113 mm，0.062°）。由此说明，BAS-PSO算法辨识得到的机器人运动学模型的泛化能力相比其他两种算法较好。

4.2　运动学误差模型精度分析

前文已介绍机器人运动学误差模型的两种建模方法，理论上在建立基于位姿微分变换的运动学误差模型过程中，仅作一次高阶项忽略；而建立基于坐标误差传递的运动学误差模型时，做两次高阶项忽略。因此，基于位姿微分变换的运动学误差模型的精度理论上要优于基于坐标误差传递的运动学误差模型。同时，由于智能优化算法不用必须建立误差模型，本文可直接利用式（4）构建的正运动学模型辨识M-DH运动学模型参数，此种方式未做任何误差忽略，其理论精度会比其他两种误差模型高。

由于BAS-PSO是一种随机优化算法，其辨识结果具有一定的随机性，主要体现在初始种群选取及个体位置更新。为评价误差模型的标定效果，本文利用相同的数据集对3种模型分别标定10次，标定结果如图7所示。为评价模型的性能，本文利用平均位置误差（Average Position Error，APE）和平均姿态误差（Average Attitude Error，AAE）作为评价指标，其计算公式如下：

\{\begin{array}{l} R_{A P E} = \frac{1}{N M} \sum_{i = 1}^{N} \sum_{j = 1}^{M} \sqrt[]{(Δ x^{2} + Δ y^{2} + Δ z^{2})} \\ R_{A A E} = \frac{1}{N M} \sum_{i = 1}^{N} \sum_{j = 1}^{M} \sqrt[]{(Δ α^{2} + Δ β^{2} + Δ γ^{2})} \end{array}

从图7可以看出，基于运动学模型辨识的实际运动学模型的精度更为稳定，而基于位姿微分变换的运动学误差模型和基于坐标误差传递的运动学误差模型辨识得到的实际运动学模型的精度稳定性较差。其中，基于坐标误差传递的运动学误差模型（误差模型1）辨识后的机器人APE和AAE分别为0.103 5 mm和0.164 2°，基于位姿微分变换的运动学误差模型（误差模型2）辨识后的机器人APE和AAE分别为0.100 9 mm和0.156 5°，而基于正运动学模型（误差模型3）直接辨识后的机器人APE和AAE分别为0.097 5 mm和0.098 6°。因此，基于正运动学模型直接辨识的机器人精度更高。

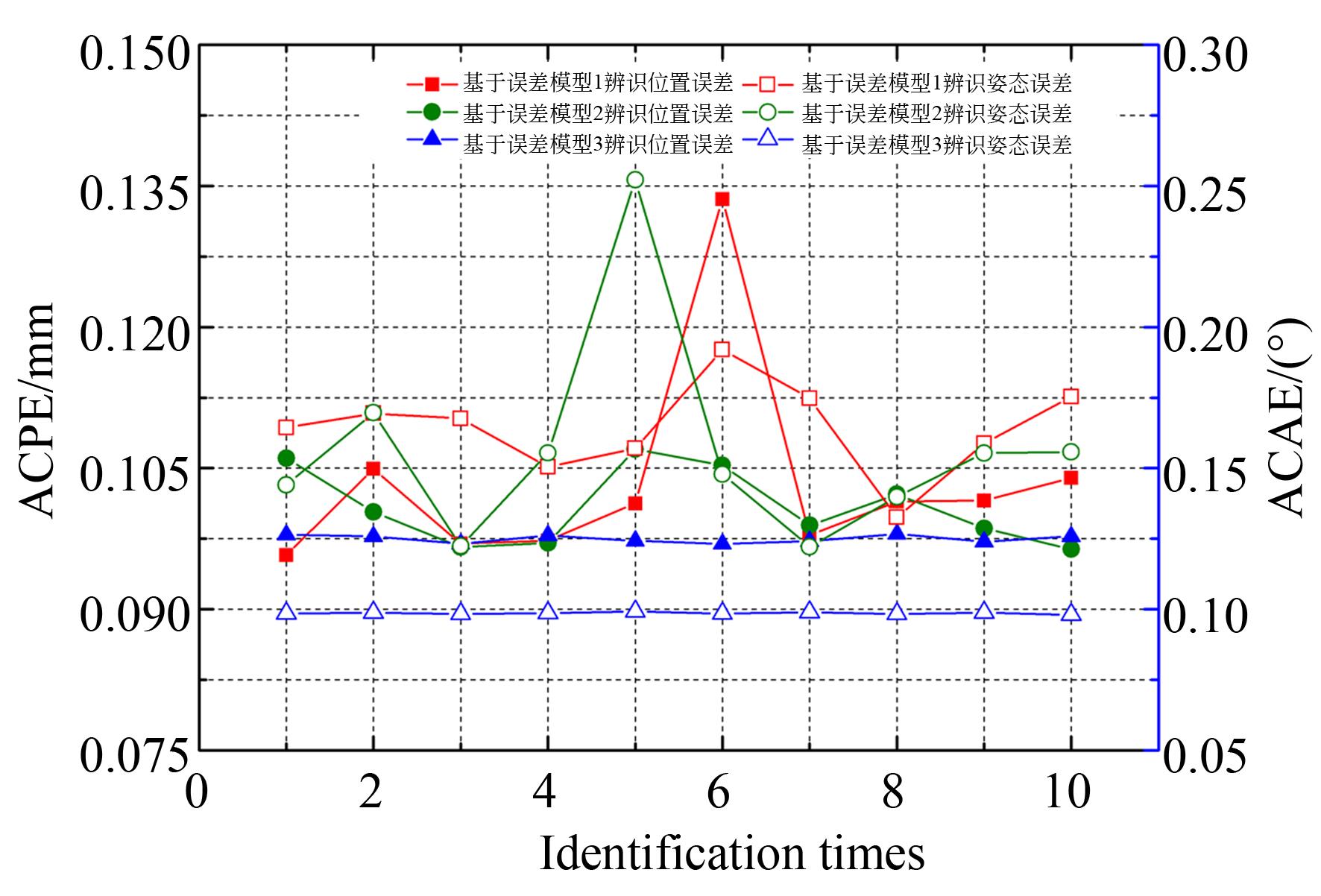
图 7. 不同误差模型辨识后平均综合位置/姿态误差的对比

Fig. 7. Comparison of average comprehensive position and attitude errors(ACPE/ACAE) after identification with different error models

下载图片查看所有图片

5 结　论

本文首先阐述了工业机器人基于位姿微分变换的运动学误差模型和基于坐标误差传递的运动学误差模型的构建方法；其次，提出了一种基于BAS-PSO算法的运动学参数辨识方法，相比于PSO和BAS算法，该算法具有更好的辨识精度和收敛速度。实验结果表明，经该算法辨识后TX60机器人的ACPE，ACAE分别从（0.312 mm，0.221°）降低为（0.093 8 mm，0.044 2°）。最后，分析了基于位姿微分变换的运动学误差模型、基于坐标误差传递的运动学误差模型以及基于正运动学模型在机器人运动学参数辨识中的精度特性。从实验结果可以看出，基于正运动学模型辨识的机器人运动学参数具有更好的稳定性和精度，而基于坐标误差传递的运动学误差模型辨识的机器人运动学参数精度相对较差。

参考文献

[1] MEJRIS， GAGNOLV， LET P， et al. Dynamic characterization of machining robot and stability analysis［J］. The International Journal of Advanced Manufacturing Technology， 2016， 82（1/2/3/4）： 351-359.

[2] JIAO J C, TIAN W, LIAO W H, et al. Processing configuration off-line optimization for functionally redundant robotic drilling tasks[J]. Robotics and Autonomous Systems, 2018, 110: 112-123.

[3] 杨守瑞，尹仕斌，任永杰，等. 机器人柔性视觉测量系统标定方法的改进［J］. 光学精密工程， 2014， 22（12）： 3239-3246.YANGSH R， YINSH B， RENY J， et al. Improvement of calibration method for robotic flexible visual measurement systems［J］. Opt. Precision Eng.， 2014， 22（12）： 3239-3246.（in Chinese）

[4] NUBIOLA A, BONEV I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(1): 236-245.

[5] 邾继贵，张楠楠，任永杰，等. 基于双目立体视觉的工业机器人在线温度补偿［J］. 光学精密工程， 2018， 26（9）： 2139-2149.ZHUJ G， ZHANGN N， RENY J， et al. In-line thermal compensation of industrial robots based on binocular stereo vision［J］. Opt. Precision Eng.， 2018， 26（9）： 2139-2149.（in Chinese）

[6] JUDD R P, KNASINSKI A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE Transactions on Robotics and Automation, 1990, 6(1): 20-30.

[7] 许允斗，王超，赵春霖，等. 2RPU/UPR+RP五自由度混联机器人参数标定研究［J］. 光学精密工程， 2020， 28（1）： 119-129.XUY D， WANGCH， ZHAOCH L， et al. Parameter calibration of five-degree-of-freedom hybrid robot 2RPU/UPR+RP［J］. Opt. Precision Eng.， 2020， 28（1）： 119-129.（in Chinese）

[8] SANTOLARIAJ， CONTEJ， GINÉSM. Laser tracker-based kinematic parameter calibration of industrial robots by improved CPA method and active retroreflector［J］. The International Journal of Advanced Manufacturing Technology， 2013， 66（9/10/11/12）： 2087-2106.

[9] CHEN-GANG， LI-TONG， CHU-MING，, et al. Review on kinematics calibration technology of serial robots[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(8): 1759-1774.

[10] 洪鹏，田威，梅东棋，等. 空间网格化的机器人变参数精度补偿技术［J］. 机器人， 2015， 37（3）： 327-335.HONGP， TIANW， MEID Q， et al. Robotic variable parameter accuracy compensation using space grid［J］. Robot， 2015， 37（3）： 327-335.（in Chinese）

[11] 陈钢，贾庆轩，李彤，等. 基于误差模型的机器人运动学参数标定方法与实验［J］. 机器人， 2012， 34（6）： 680-688.CHENG， JIAQ X， LIT， et al. Calibration method and experiments of robot kinematics parameters based on error model［J］. Robot， 2012， 34（6）： 680-688.（in Chinese）

[12] 杨聚庆，王大勇，董登峰，等. 激光测量标定机器人坐标系位姿变换的正交化解算［J］. 光学精密工程， 2018， 26（8）： 1985-1993.YANGJ Q， WANGD Y， DONGD F， et al. Laser measurement based evaluation for orthogonal transformation calibration of robot pose［J］. Opt. Precision Eng.， 2018， 26（8）： 1985-1993.（in Chinese）

[13] 李辉，刘巍，张洋，等. 激光跟踪仪多基站转站精度模型与误差补偿［J］. 光学精密工程， 2019， 27（4）： 771-773.LIH， LIUW， ZHANGY， et al. Model establishment and error compensation of laser tracker station-transfer［J］. Opt. Precision Eng.， 2019， 27（4）： 771-773.（in Chinese）

[14] MA L, BAZZOLI P, SAMMONS P M, et al. Modeling and calibration of high-order joint-dependent kinematic errors for industrial robots[J]. Robotics and Computer-Integrated Manufacturing, 2018, 50: 153-167.

[15] YU L. Calibration of a 6-DOF space robot using genetic algorithm[J]. Chinese Journal of Mechanical Engineering (English Edition), 2008, 21(6): 6.

[16] 房立金，党鹏飞. 基于量子粒子群优化算法的机器人运动学标定方法［J］. 机械工程学报， 2016， 52（7）： 23-30.FANGL J， DANGP F. Kinematic calibration method of robots based on quantum-behaved particle swarm optimization［J］. Journal of Mechanical Engineering， 2016， 52（7）： 23-30.（in Chinese）

[17] 温秀兰，康传帅，宋爱国，等. 基于全位姿测量优化的机器人精度研究［J］. 仪器仪表学报， 2019， 40（7）： 81-89.WENX L， KANGCH SH， SONGA G， et al. Study on robot accuracy based on full pose measurement and optimization［J］. Chinese Journal of Scientific Instrument， 2019， 40（7）： 81-89.（in Chinese）

[18] HAYATI S, MIRMIRANI M. Improving the absolute positioning accuracy of robot manipulators[J]. Journal of Robotic Systems, 1985, 2(4): 397-413.

[19] JIANG X, LI S. BAS: Beetle Antennae Search Algorithm for Optimization Problems[J]. International Journal of Robotics & Control, 2018, 1(1): 1-3.

[20] MAARANEN H, MIETTINEN K, MÄKELÄ M M. Quasi-random initial population for genetic algorithms[J]. Computers & Mathematics With Applications, 2004, 47(12): 1885-1895.

4.1　基于BAS-PSO的运动学参数辨识

4.2　运动学误差模型精度分析

5 结　论

乔贵方, 吕仲艳, 张颖, 宋光明, 宋爱国. 基于BAS-PSO算法的机器人定位精度提升[J]. 光学精密工程, 2021, 29(4): 763. Gui-fang QIAO, Zhong-yan LÜ, Ying ZHANG, Guang-ming SONG, Ai-guo SONG. Improvement of robot kinematic accuracy based on BAS-PSO algorithm[J]. Optics and Precision Engineering, 2021, 29(4): 763.

基于BAS-PSO算法的机器人定位精度提升下载： 807次

1 引　言

2 机器人运动学误差模型建立

2.1　建立M-DH运动学模型

图 1. 非平行关节(a)与平行关节(b)的坐标系转换

Fig. 1. Coordinate transformation between non-parallel joints (a) and parallel joints (b)

表 1. Staubli TX60机器人M-DH运动学模型的名义参数

Table 1. Nominal parameters of M-DH kinematics model of Staubli TX60 robot

2.2　基于位姿微分变换的运动学误差模型

2.3　基于坐标误差传递的运动学误差模型

3 基于BAS-PSO的运动学参数辨识

3.1　BAS-PSO混合优化算法

图 2. 天牛须搜索算法的仿生原理示意图

Fig. 2. Schematic diagram of bionic principle for beetle antennae search algorithm

3.2　误差模型的适应度函数

4 运动学参数辨识实验

图 3. 工业机器人标定系统

Fig. 3. Photo of industrial robot calibration system

4.1　基于BAS-PSO的运动学参数辨识

图 4. 不同优化算法的计算过程对比

Fig. 4. Calculation process comparison of different optimization algorithms

图 5. 标定前后机器人的平均综合位置误差

Fig. 5. Average comprehensive position errors（ACPE） of robot before and after calibration

图 6. 标定前后机器人的平均综合姿态误差

Fig. 6. Average comprehensive attitude error（ACAE） of robot before and after calibration

4.2　运动学误差模型精度分析

图 7. 不同误差模型辨识后平均综合位置/姿态误差的对比

Fig. 7. Comparison of average comprehensive position and attitude errors(ACPE/ACAE) after identification with different error models

5 结　论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

基于BAS-PSO算法的机器人定位精度提升 下载： 807次

1 引 言

2 机器人运动学误差模型建立

2.1 建立M-DH运动学模型

图 1. 非平行关节(a)与平行关节(b)的坐标系转换

Fig. 1. Coordinate transformation between non-parallel joints (a) and parallel joints (b)

表 1. Staubli TX60机器人M-DH运动学模型的名义参数

Table 1. Nominal parameters of M-DH kinematics model of Staubli TX60 robot

2.2 基于位姿微分变换的运动学误差模型

2.3 基于坐标误差传递的运动学误差模型

3 基于BAS-PSO的运动学参数辨识

3.1 BAS-PSO混合优化算法

图 2. 天牛须搜索算法的仿生原理示意图

Fig. 2. Schematic diagram of bionic principle for beetle antennae search algorithm

3.2 误差模型的适应度函数

4 运动学参数辨识实验

图 3. 工业机器人标定系统

Fig. 3. Photo of industrial robot calibration system

4.1 基于BAS-PSO的运动学参数辨识

图 4. 不同优化算法的计算过程对比

Fig. 4. Calculation process comparison of different optimization algorithms

图 5. 标定前后机器人的平均综合位置误差

Fig. 5. Average comprehensive position errors（ACPE） of robot before and after calibration

图 6. 标定前后机器人的平均综合姿态误差

Fig. 6. Average comprehensive attitude error（ACAE） of robot before and after calibration

4.2 运动学误差模型精度分析

图 7. 不同误差模型辨识后平均综合位置/姿态误差的对比

Fig. 7. Comparison of average comprehensive position and attitude errors(ACPE/ACAE) after identification with different error models

5 结 论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于BAS-PSO算法的机器人定位精度提升下载： 807次

1 引　言

2.1　建立M-DH运动学模型

2.2　基于位姿微分变换的运动学误差模型

2.3　基于坐标误差传递的运动学误差模型

3.1　BAS-PSO混合优化算法

3.2　误差模型的适应度函数

4.1　基于BAS-PSO的运动学参数辨识

4.2　运动学误差模型精度分析

5 结　论