0 引　言

大型运输船舶是远洋运载的重要平台，长周期、高能耗地航行于复杂多变的海洋环境下，因而船舶的安全、节能以及高效航行就显得极为重要^[1]。在运动控制领域，船舶的大排水量、高稳心属于大时滞系统，在高海况条件下极易造成船舶的倾覆，可见运动响应是需要解决的瓶颈问题之一。随着人工智能、大数据等各类新技术在海洋装备领域的应用，海上运输船舶的高性能化、高技术化发展趋势愈加显著，聚焦于控制算法的演进、寻求约束条件下更优的艏向瞬态和稳态跟踪性能，以及更好的自适应性能成为智能自主航行重要的方向之一。

有关大型运输船舶运动控制的相关研究比较多。例如，张显库等^[1]针对恶劣海况下智能运输船舶的航行安全问题，提出了一种鲁棒控制算法；金仲佳等^[2]针对高海况下的船舶减摇和效能提升问题，设计了一种分频线性二次型最优（FDLQR）舵减横摇控制器，实现了快速跟踪响应；Borkowski^[3]为确定复杂时变环境下船舶的控制参数，提出了一种基于线性二次型调节器（LQR）的船舶自适应控制系统，结果显示控制质量良好；李明聪等^[4]针对外界干扰情况下大型无人运输船舶的航迹控制问题，基于滑模控制方法和反步法，设计了一种反步滑模控制器；Lee等^[5]为保证船舶在恶劣海况下的垂直位置，采用自适应分数阶滑模控制（AFOSMC）方法对船舶纵摇进行有效调节，保证了船舶纵摇系统的闭环稳定性。以上文献充分利用了LQR控制方法所具有的良好的稳定裕度和响应速度的优势^[6]，以及滑模控制方法对系统模型的不确定性和外界干扰不敏感的特点，有效解决了外界干扰或极端工况下船舶航行的安全性和控制稳定性问题。

近年来，为解决复杂时变环境下的自适应控制问题，一类模拟自然界生物群体行为特征的群智能优化算法，如蜻蜓算法^[7]（DA）、蚁狮优化算法^[8]（ALO）、鲸鱼优化算法^[9]（WOA）被用于不同工况控制参数的自动寻优。Saremi等^[10]于2017年提出了蝗虫优化的群智能优化算法，并将其应用到了参数优化问题中。蝗虫优化算法（GOA）结构简单、参数少、稳定性较强，在寻优精度和求解速度上具有很强的竞争力^[11]，且算法本身特殊的自适应机制能够很好地平衡全局和局部搜索过程^[12]。为此，本文拟基于GOA，通过综合权衡船舶安全、节能和精确控制要求，将LQR控制和一阶动态积分滑模控制相结合形成一种新的控制方法，从而实现大型运输船舶在不同海况下的安全自适应航行。

1 大型运输船舶运动数学模型

对于水面大型运输船舶而言，由海洋环境因素造成的船舶影响主要包含2个部分：一是由风、流及二阶波浪力产生的慢运动，其会使船舶缓慢地漂离原来的位置；二是由一阶波浪力产生的高频往复运动，控制该高频运动会加速推力器系统的磨损和对能量的消耗，并且这种高频运动还会影响传感器的测量精度，故须滤掉高频分量。所以，系统不仅要剔除来自传感器信息中的高频运动分量和噪声，还要利用预估值实现对低频运动的准确控制。为实现上述目的，本文拟将船舶的高频运动和低频运动分开处理。

1.1 船舶低频运动模型

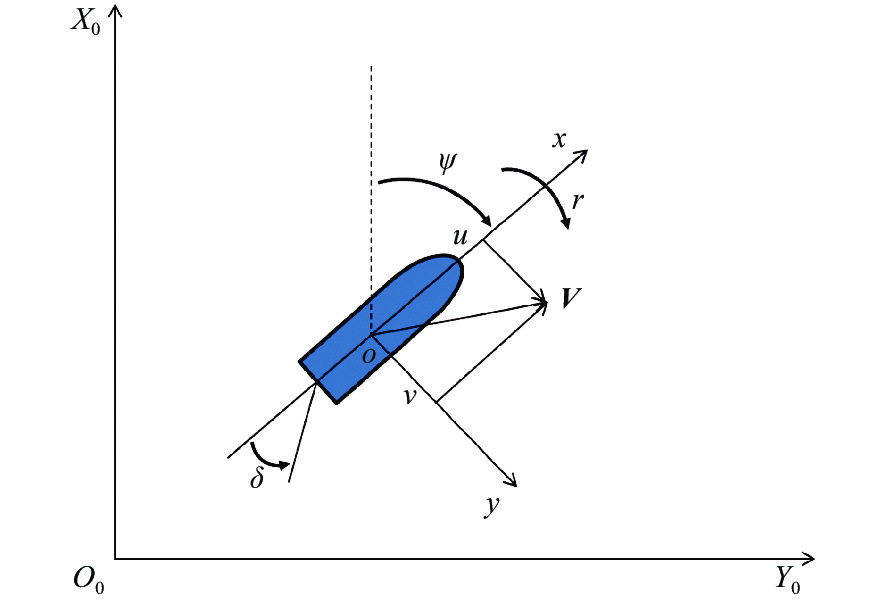
在低海况条件下，大型船舶的纵摇、横摇和升沉运动对其在水平面内的运动影响较小，可忽略不计，因此，将其运动简化为3个自由度的平面运动。如图1所示，要研究船舶运动的数学模型，通常需要建立附体坐标系$xoy$和惯性坐标系${X_0}{O_0}{Y_0}$，附体坐标系取船体的重心为原点。图中：${\boldsymbol{V}} = [ u\;\;v\;\;r ]$，为船舶的线速度和角速度向量，其中$u$，$v$，$r$分别为附体坐标系下的纵荡速度、横荡速度和转艏角速度；$\psi $为艏向角；$\delta $为舵角。

图 1. The relationship between ship's body-fixed and inertial coordinate systems船舶平面附体坐标系与惯性坐标系之间的关系

Fig. 1.

下载图片 查看所有图片

大型运输船舶所受的力主要有惯性水动力、黏性水动力、螺旋桨推力、舵力以及环境干扰力^[13]。基于船舶操纵运动数学模型研究小组的标准方法，将各自由度的动力学特性进行解耦处理，每个独立系统的水动力方程均具有物理意义^[14]。大型船舶的状态变量为$ {\boldsymbol{x}} = [u\;\;v\;\;r\;\;x\;\;y\;\;\psi ] $，控制输入量为$\delta $。建立如下三自由度水平面运动船舶的纵荡、横荡、艏摇非线性动力学方程：

$ \begin{split} & \qquad\qquad\quad m\left( {\dot u - vr} \right)+\left( {{m_x}\dot u - {m_y}vr} \right) = \\ &\quad {X_{\rm{S}}} + \left( {1 - {t_{\rm{p}}}} \right)\rho {n^2}D_{\rm{p}} ^4{K_{\rm{T}}}\left( J \right) + \left( {1 - {t_{\rm{R}}}} \right){F_{\rm{N}}}\sin \delta + {X_{{\text{ENV}}}} \\ & {m\left( {\dot v + ur} \right){\text{ + }}\left( {{m_y}\dot v + {m_x}ur} \right) = {Y_{\rm{S}}} + \left( {1 + {a_{\rm{H}}}} \right){F_{\rm{N}}}\cos \delta + {Y_{{\text{ENV}}}}} \\ & \qquad {{I_{\textit{z}}}\dot r{\text{ + }}{J_{\textit{z}}}\dot r = {N_{\rm{S}}} + \left( {{x_{\rm{R}}} + {a_{\rm{H}}}{x_{\rm{H}}}} \right){F_{\rm{N}}}\cos \delta + {Z_{{\text{ENV}}}}} \end{split}$ (1)

式中：$m$为船舶质量；${m_x}$，${m_y}$为$x$，$y$轴上的附加质量；${X_{\rm{S}}}$，${Y_{\rm{S}}}$，${N_{\rm{S}}}$分别为船舶的纵荡、横荡和艏摇水动力方程；${t_{\rm{p}} }$为推力减额系数；${t_{\rm{R}}}$为舵阻力减额系数；$ \rho $为海水密度；$n$为螺旋桨转速；${D_{\rm{p}} }$为螺旋桨直径；${K_{\rm{T}}}\left( J \right)$为螺旋桨的推力系数，其中$J$为螺旋桨进速系数；${F_{\rm{N}}}$为垂直于舵叶平面的正压力；${X_{{\text{ENV}}}}$，${Y_{{\text{ENV}}}}$，${Z_{{\text{ENV}}}}$分别为风、流及二阶波浪等环境干扰产生的纵向力、横向力及旋转力矩；${a_{\rm{H}}}$为操舵诱导船体横向力的修正系数；${I_{\textit{z}}}$为绕$o{\textit{z}}$轴的转动惯量；${J_{\textit{z}}}$为绕$\textit{z}$轴的附加转动惯性矩；${x_{\rm{R}}}$为作用于舵上横向力的纵坐标；${x_{\rm{H}}}$为操舵诱导船体横向力作用中心至船舶重心的距离，取值约为−0.45$L$。

${X_{\rm{S}}}$，${Y_{\rm{S}}}$，${N_{\rm{S}}}$的表达式分别如下：

$ \begin{array}{*{20}{c}} {{X_{\rm{S}}} = {X_{\left( u \right)}} + {X_{vv}}{v^2} + {X_{vr}}vr + {X_{rr}}{r^2}} \\ {{Y_{\rm{S}}} = {Y_v}v + {Y_r}r + {Y_{\left| v \right|v}}\left| v \right|v + {Y_{\left| r \right|r}}\left| r \right|r + {Y_{vvr}}{v^2}r + {Y_{vrr}}v{r^2}} \\ {{N_{\rm{S}}} = {N_v}v + {N_r}r + {N_{\left| v \right|v}}\left| v \right|v + {N_{\left| r \right|r}}\left| r \right|r + {N_{vvr}}{v^2}r + {N_{vrr}}v{r^2}} \end{array} $ (2)

式中：${X_{\left( u \right)}}$为直航阻力；${Y_v}v$，${Y_r}r$和${N_v}v$，${N_r}r$分别为线性横向水动力及力矩；${X_{vv}}{v^2}$，${X_{vr}}vr$，${X_{rr}}{r^2}$为船舶引起的黏性阻力；$ {Y_{\left| v \right|v}}\left| v \right|v $，$ {Y_{\left| r \right|r}}\left| r \right|r $，${Y_{vvr}}{v^2}r$，${Y_{vrr}}v{r^2}$和$ {N_{\left| v \right|v}}\left| v \right|v $，$ {N_{\left| r \right|r}}\left| r \right|r $，${N_{vvr}}{v^2}r$，${N_{vrr}}v{r^2}$分别为非线性横向水动力及力矩。

建立船舶在水平面的运动学和动力学模型如下：

$ \left\{ \begin{aligned} & {\dot u = \frac{{\left( {m + {m_y}} \right)vr + {X_{\rm{S}}} + \left( {1 - {t_{\rm{p}}}} \right)\rho {n^2}D_{\rm{p}} ^4{K_{\rm{T}}}\left( J \right) + \left( {1 - {t_{\rm{R}}}} \right){F_{\rm{N}}}\sin \delta + {X_{{\text{ENV}}}}}}{{\left( {m + {m_x}} \right)}}} \\& {\dot v = \frac{{ - \left( {m + {m_x}} \right)ur + {Y_{\rm{S}}} + \left( {1 + {a_{\rm{H}}}} \right){F_{\rm{N}}}\cos \delta + {Y_{{\text{ENV}}}}}}{{\left( {m + {m_y}} \right)}}} \\& {\dot r = \frac{{{N_{\rm{S}}} + \left( {{x_{\rm{R}}} + {a_{\rm{H}}}{x_{\rm{H}}}} \right){F_{\rm{N}}}\cos \delta + + {Z_{{\text{ENV}}}}}}{{\left( {{I_{\textit{z}}} + {J_{\textit{z}}}} \right)}}} \\& {\dot x = u\cos \psi - v\sin \psi } \\& {\dot y = u\sin \psi + v\cos \psi } \\& {\dot \psi = r} \end{aligned}\right. $ (3)

1.2 船舶高频运动模型

船舶高频运动来自于一阶波浪力产生的高频往复运动。Saelid等^[15]在波浪模型中引入了阻尼项，用以更好地拟合Pierson-Moskowitz波谱的形状，该波浪模型为

$ h\left( s \right) = \frac{{{K_\omega }s}}{{{s^2} + 2\lambda {\omega _{\rm{o}}}s + \omega _{\rm{o}} ^2}} $ (4)

式中：$ {K_\omega } $为增益常数，${K_\omega }{\text{ = }}2\lambda {\omega _{\rm{o}}}I$，其中$I$为描述波浪强度的系数；$\lambda $为相对阻尼比；${\omega _{\rm{o}}}$为波浪主导频率；$s$为复频率。

将式（4）转换为状态空间形式，得到船舶的高频运动模型为

$ \left\{ \begin{aligned} & {{\dot \xi }_{\text{h}}} = {{\boldsymbol{A}}_{\text{h}}}{\xi _{\text{h}}} + {{\boldsymbol{E}}_{\text{h}}}{\omega _{\text{h}}} \\& {\eta _{\text{h}}} = {{\boldsymbol{C}}_{\text{h}}}{\xi _{\text{h}}} \end{aligned}\right. $ (5)

式中：${\dot \xi _{\text{h}}} = \left[ {{{\dot \xi }_\psi }}\;\;{{{\dot \psi }_{\text{h}}}} \right]$，其中${\dot \xi _\psi }$，${\dot \psi _{\text{h}}}$分别为船舶在艏摇方向上的位置和速度；${\omega _{\text{h}}}$为零均值高斯白噪声；${\eta _{\text{h}}}$为船舶高频运动时的艏向角；${{\boldsymbol{A}}_{\text{h}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 0&1 \\ { - \omega _{\rm{o}} ^2}&{ - 2\lambda {\omega _{\rm{o}}}} \end{array}} \right]$；${{\boldsymbol{E}}_{\text{h}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 0 \\ {{K_\omega }} \end{array}} \right]$；${{\boldsymbol{C}}_{\text{h}}}{\text{ = }}\left[ 0\;\;1 \right]$。

2 控制器设计

LQR最优控制通常用于表征在多个特定的约束条件下得到性能指标最优解，适用于系统多目标优化的控制问题。滑模控制拥有能克服参数扰动的优势，对非线性系统有着良好的控制效果，但可能存在控制抖动。

本文基于GOA，通过综合LQR最优控制和滑模控制的优点，设计了一种大型运输船舶的自适应控制系统，控制原理框图如图2所示。控制系统的输出为$x$，$y$，$\psi $，输入为指令艏向角${\psi _{\text{d}}}$，${\psi _\omega }$为由一阶波浪引起的艏向角变化，${\boldsymbol{h}}\left( k \right)$为由一阶波浪模型输入输出数据构成的信息向量。首先，采用基于递推最小二乘法估计器的非线性无源估计器对大型运输船舶的运动进行实时状态估计，然后将艏向角跟踪误差估计值$\hat e = {\psi _{\text{d}}} - \hat \psi $和转艏角速度估计值$\hat r$作为自适应调节的输入，设计一种基于GOA、将LQR控制方法和一阶动态积分滑模控制方法进行混合的自适应控制器，最后通过自适应调节计算指令舵角$\delta $，使跟踪误差估计值$\hat e$趋于0，最终实现船舶的艏向跟踪控制。

图 2. Schematic diagram of large transport ship motion control大型运输船舶运动控制原理图

Fig. 2.

下载图片 查看所有图片

采用LQR控制结构的输出值${u_{\rm{LQR}}}$和一阶动态积分滑模控制结构的输出值${u_{\rm{SMC} }}$，经GOA综合权衡船舶安全性、节能以及稳态控制精度等约束条件，进行最优解位置的在线调整，即可获取船舶在不同工况条件下的自适应控制参数^[16]。

2.1 估计器

本文采用递推最小二乘法与非线性无源估计器相结合的方法进行船舶艏向角和转艏角速度的在线辨识。非线性无源估计器是一种具有滤波处理和状态估计的方法^[17]，对测量噪声具有强鲁棒性，但无法满足高精度系统控制要求，因此需要结合递推最小二乘法在线获取非线性无源估计器所需的波谱相对阻尼比和波浪主导频率，建立更精准的估计器模型，剔除高频运动分量和噪声，从而获取准确的艏向角和转艏角速度信息，实现对船舶运动的高精度控制。

2.1.1 非线性无源估计器

非线性无源估计器能将处于波浪力作用下的船舶水平运动中的低频运动和高频运动分离，滤除由一阶波浪引起的船舶高频运动，估算出船舶低频运动状态，从而使大型运输船舶的艏向角能够更加精确地到达期望位置。

建立估计器模型如下：

$ \begin{split} & {\dot{\hat{\xi }}}_{\omega }={\hat{\psi }}_{\omega }+{K}_{1}\left(\psi -\hat{\psi }\right)\\& {\dot{\hat{\psi }}}_{\omega }=-{\omega }_{\mathrm{o}}^{2}{\hat{\xi }}_{\omega }-2\lambda {\omega }_{\mathrm{o}}{\hat{\psi }}_{\omega }+{K}_{2}\left(\psi -\hat{\psi }\right)\\& \dot{\hat{\psi }}=\hat{r}+{K}_{3}\left(\psi -\hat{\psi }\right)\\& \dot{\hat{r}}=-\dfrac{1}{T}\hat{r}+\dfrac{K}{T}\hat{b}+{K}_{4}\left(\psi -\hat{\psi }\right)\\& \dot{\hat{b}}=-\dfrac{1}{{T}_{\mathrm{b}}}\hat{b}+{K}_{5}\left(\psi -\hat{\psi }\right) \end{split} $ (6)

式中：${\xi _\omega }$为多个谐波分量之和；$ {K_1} $，$ {K_2} $，$ {K_3} $，$ {K_4} $，$ {K_5} $为观测增益；$T$，$K$分别为野本时间常数和野本增益；$b$为低频的干扰力；${T_{\rm{b}} }$为舵偏移时间常数。

2.1.2 递推最小二乘法估计器

利用递推最小二乘法估计器，对非线性无源估计器所需的波谱相对阻尼比和波浪主导频率进行实时观测。最小二乘法的基本思路是：对模型进行变换，对波浪模型（式（4））进行Z变换（式（7）），然后利用递推最小二乘法估计器的数学模型（式（9））估计出式（8）所示的当前时刻参数，再对式（8）进行S变换得到波浪的在线估计模型，最后，将实时观测到的波谱相对阻尼比和波浪主导频率信息传递到非线性无源估计器，得到观测增益的实时值，使估计器模型更精确并具有实时性。

将式（4）离散化为最小二乘回归模型：

$ {\boldsymbol{z}}\left( k \right) = {{\boldsymbol{h}}^{\rm{T}}}\left( k \right){\boldsymbol{\theta}} $ (7)

式中：${\boldsymbol{z}}\left( k \right)$为系统输出向量；${\boldsymbol{\theta}} {\text{ = }}\left[ {{a_1}}\;\;{{a_2}}\;\;{{a_3}}\;\;{{a_4}} \right]$，为待估计的模型参数向量。

对于一般的离散非线性时变系统，式（7）可以表示为

$ \begin{split} & {\boldsymbol{z}}\left( k \right) = {a_1}{\boldsymbol{u}}\left( {k - 1} \right) + {a_2}{\boldsymbol{u}}\left( {k - 2} \right) + {a_3}{\boldsymbol{z}}\left( {k - 1} \right) + {a_4}{\boldsymbol{z}}\left( {k - 2} \right)\\&\; \end{split} $ (8)

式中，${\boldsymbol{u}}\left( k \right)$为系统输入向量。

最小二乘法的递推公式为：

$ \begin{split} & {\hat {\boldsymbol{\theta}} ( k ) = \hat {\boldsymbol{\theta}} ( {k - 1} ) + {\boldsymbol{K}}( k )[ {{\boldsymbol{z}}( k ) - {{\boldsymbol{h}}^{\rm{T}}}( k )\hat {\boldsymbol{\theta}} ( {k - 1} )} ]} \\& {{\boldsymbol{K}}( k ) = {\boldsymbol{P}}( {k - 1} ){\boldsymbol{h}}( k ){{[ {{{\boldsymbol{h}}^{\rm{T}}}( k ){\boldsymbol{P}}( {k - 1} ){\boldsymbol{h}}( k ) + 1} ]}^{ - 1}}} \\ & {{\boldsymbol{P}}( k ) = [ {{\boldsymbol{I}} - {\boldsymbol{K}}( k ){{\boldsymbol{h}}^{\rm{T}}}( k )} ]{\boldsymbol{P}}( {k - 1} )} \end{split} $ (9)

式中：$ {\boldsymbol{K}}\left( k \right) $为增益矩阵；$ {\boldsymbol{P}}\left( k \right) $为协方差矩阵；${\boldsymbol{ I}} $为单位矩阵。

2.2 LQR最优控制

建立大型运输船舶艏向控制系统的状态空间方程如下：

$ \begin{split} & {{{\dot {\boldsymbol{x}}}_{\text{L}}} = {\boldsymbol{A}}{{\boldsymbol{x}}_{\text{L}}} + {\boldsymbol{B}}{u_{\rm{LQR}}}} \\ & {{y_{\text{L}}} = {\boldsymbol{C}}{{\boldsymbol{x}}_{\text{L}}}} \end{split}$ (10)

式中：${{\boldsymbol{x}}_{\text{L}}} = {[ \psi \;\; r ]^{\rm{T}}}$，为状态向量；${u_{\rm{LQR}}}$为控制量；$ {y_{\text{L}}} $为系统的输出；系统中的$ {\boldsymbol{A}} $，$ {\boldsymbol{B}} $，$ {\boldsymbol{C}} $必须是可控的矩阵。

通过考虑状态空间模型来设计一种LQR，目的是使控制器跟踪期望的输出y_d，将误差$e = {y_{\text{L}}} - {y_{\text{d}}}$降至0，同时，为取得最优控制${u_{\rm{LQR}}}$，使二次型目标函数$ J $取得极小值。

$ J = \frac{1}{2}\mathop \int \nolimits_0^{\rm{T}} \left( {{e^{\rm{T}}}{\boldsymbol{Q}}e + u_{\rm{LQR}}^{\rm{T}}{\boldsymbol{R}}{u_{\rm{LQR}}}} \right){{\rm{d}}}t $ (11)

式中，${\boldsymbol{Q}} = {{\boldsymbol{Q}}^{\rm{T}}} > 0$，$ {\boldsymbol{ R}}={{\boldsymbol{R}}}^{\rm{T}} > 0 $，分别为半正定的状态加权和正定的控制加权矩阵，两者通常取为对角矩阵。得到LQR的最优控制律为

$ {u_{\rm{LQR}}} = - {{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}}{{\boldsymbol{x}}_{\text{L}}} $ (12)

式中，${\boldsymbol{P}}$为正定的实对称方阵，满足Riccati代数方程${\boldsymbol{PA}}{\text{ + }}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{P}} - {\boldsymbol{PB}}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}} = - {\boldsymbol{Q}}$的解。

考虑李雅普诺夫函数：

$ {V_{\rm{LQR}}} = {\boldsymbol{x}}_{\text{L}}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{x}}_{\text{L}}} $ (13)

选择输出${u_{{\text{LQR}}}} = {\boldsymbol{K}}{{\boldsymbol{x}}_{\text{L}}}$，最优反馈系数矩阵${\boldsymbol{K}} = - {{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}}$。

对${V_{\rm{LQR}}}$求导，得

$ \begin{split} & \qquad\qquad{{\dot V}_{\rm{LQR}}} = \dot {\boldsymbol{x}}_{\text{L}}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{x}}_{\text{L}}} + {\boldsymbol{x}}_{\text{L}}^{\text{T}}{\boldsymbol{P}}{{\dot x}_{\text{L}}} =\\&\;\;\;\; {\boldsymbol{x}}_{\text{L}}^{\text{T}}( {{{\boldsymbol{A}}^{\rm{T}}} - {{\boldsymbol{K}}^{\rm{T}}}{{\boldsymbol{B}}^{\rm{T}}}} ){\boldsymbol{P}}{{\boldsymbol{x}}_{\text{L}}} + {\boldsymbol{x}}_{\text{L}}^{\text{T}}{\boldsymbol{P}}( {{\boldsymbol{A}} - {\boldsymbol{BK}}} ){{\boldsymbol{x}}_{\text{L}}} = \\&\quad\;\;\;\; {\boldsymbol{x}}_{\text{L}}^{\text{T}}( {{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{P}} + {\boldsymbol{PA}} - {{\boldsymbol{K}}^{\rm{T}}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}} - {\boldsymbol{PBK}}} ){\boldsymbol{x}}{_{\text{L}}} = \\& {\boldsymbol{x}}_{\text{L}}^{\text{T}}( { - {\boldsymbol{Q}} + {\boldsymbol{PB}}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}} - {{\boldsymbol{K}}^{\rm{T}}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}} - {\boldsymbol{PBK}}} ){{\boldsymbol{x}}_{\text{L}}} = \\&\quad {\boldsymbol{x}}_{\text{L}}^{\text{T}}( { - {\boldsymbol{Q}} + {\boldsymbol{PB}}( {{{\boldsymbol{R}}^{ - 1}} - {{\boldsymbol{R}}^{ - 1}} - {{\boldsymbol{R}}^{ - 1}}} ){{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}}} ){{\boldsymbol{x}}_{\text{L}}} = \\&\qquad\qquad {\boldsymbol{x}}_{\text{L}}^{\text{T}}( { - {\boldsymbol{Q}} - {\boldsymbol{PB}}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{P}}} ){{\boldsymbol{x}}_{\text{L}}} \end{split}$ (14)

由式（14）可知，${\dot V_{\rm{LQR}}} < 0$，此时，闭环系统是稳定的。

2.3 一阶动态积分滑模控制

滑模控制对扰动不灵敏，能克服参数扰动，这对工作于复杂环境下的大型运输船舶而言有着较好的控制效果，使系统具有较好的鲁棒性。积分滑模控制能消除稳态误差，获得较好的暂态性能，而构造一阶动态滑模控制可以解决“抖振”问题。因此，将开展基于一阶动态积分滑模控制的大型运输船舶控制方法研究。

建立大型运输船舶艏向控制系统的状态空间方程如下：

$ \left[\begin{array}{c}\dot{\psi }\\ \dot{r}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& \dfrac{{N}_{r}}{{I}_{\textit{z}}-{N}_{\dot{r}}}\end{array}\right]\left[\begin{array}{c}\psi \\ r\end{array}\right]+\left[\begin{array}{c}0\\ \dfrac{-{N}_{\delta }}{{I}_{\textit{z}}-{N}_{\dot{r}}}\end{array}\right]{u}_{\rm{SMC}} $ (15)

式中，${N_r}$，${N_\delta }$，$ {N_{\dot r}} $为水动力系数。

为了减小稳态误差，在传统的滑模面中引入了跟踪误差的积分项，得到积分滑模面${s_{\rm{I}}}$为

$ {s}_{\rm{I}}=\dot{e}+{k}_{\text{P}}e+{k}_{\text{I}}{{\displaystyle \int }}_{0}^{{t}}e(t)\text{d}t $ (16)

式中：$e$为跟踪误差，$e = \psi - {\psi _{\text{d}}}$；${k_{\text{P}}} > 0$；${k_{\text{I}}} > 0$。

由于系统状态一旦到达滑模面，系统状态就会在滑模面两侧来回穿越，控制量不断发生抖动，这是滑模控制实际应用的主要障碍。为有效降低“抖振”并获得预期的性能，通过构造一阶动态滑模控制，将控制输入的不连续项转移到控制输入的一阶导数中，即可得到在时间上连续的控制输入^[18]。

滑模面的一阶导数为

$ {\dot s_{\rm{I}}} = \dot r + {k_{\text{P}}}r + {k_{\text{I}}}e $ (17)

将$s$作为系统状态，构造新的动态切换函数

$ \sigma = {\dot s_{\rm{I}}} + {\lambda _{\rm{I}}}{s_{\rm{I}}} $ (18)

式中，${\lambda _{\rm{I}}} > 0$。对$\sigma $求导，得

$ \dot \sigma = {\ddot s_{\rm{I}}} + {\lambda _{\rm{I}}}{\dot s_{\rm{I}}} $ (19)

定义李雅普诺夫函数为

$ {V_{\rm{SMC}}} = \frac{1}{2}{\sigma ^2} $ (20)

为使系统从任意初始状态出发时在有限的时间内能到达$\sigma $，选取指数趋近律，加快趋近过程，减小“抖振”。趋近律为

$ \dot{\sigma }=-\varepsilon \text{sgn}\left(\sigma \right)-k\sigma $ (21)

式中：$ \varepsilon $，$k$为正常数；${\rm{sgn}}\left( x \right)$为符号函数。

对式（20）求导，可得

$ {\dot{V}}_{\rm{SMC}}=\sigma \dot{\sigma }=-\sigma \varepsilon {\rm{sgn}}\left(\sigma \right)-k{\sigma }^{2}=-\varepsilon \left|\sigma \right|-k{\sigma }^{2} < 0 $ (22)

根据式（15）～式（21），可得动态积分控制律为

$ \begin{split} & {\dot u_{\rm{SMC}}} = \Bigg[ - \varepsilon {\rm{sgn}}\left( \sigma \right) - k\sigma - {\lambda _{\rm{I}}}\left( {\dot r + {k_{\text{P}}}r + {k_{\text{I}}}e} \right) -\\&\qquad\qquad {k_{\text{P}}}\dot r - {k_{\text{I}}}r - \frac{{{N_r}}}{{{I_{\textit{z}}} - {N_{\dot r}}}}\dot r \Bigg]/\frac{{ - {N_\delta }}}{{{I_{\textit{z}}} - {N_{\dot r}}}} \end{split}$ (23)

由式（22），可得到函数${V_{\rm{SMC}}}$满足李雅普诺夫函数的判断条件。当正常运动远离切换面时，能快速趋向切换面并达到稳定；当运动接近切换面$\sigma = 0$时，${\dot s_{\rm{I}}} + {\lambda _{\rm{I}}}{s_{\rm{I}}} = 0$是一个渐近稳定的一阶动态系统，${s_{\rm{I}}}$趋近于0，确保了系统的鲁棒性和收敛性。

2.4 GOA迭代模型

GOA是近年来新提出的一种群智能优化算法，模拟的是自然界中蝗虫的觅食行为，是一种能够模拟蝗虫之间排斥力和吸引力的数学模型。本文将利用蝗虫算法中个体间的相互影响力，将LQR控制和一阶动态积分滑模控制进行混合，然后基于环境适应性、船舶安全性以及瞬态和稳态跟踪性能等多目标要求，开展基于GOA的大型运输船舶控制方法研究，用于控制参数选择和输出的混合优化问题。在GOA中，蝗虫迭代的下个位置是根据蝗虫的当前位置和最优位置来更新的，蝗虫的位置更新模型为

$ X = c\left( {c\frac{{{b}_{\rm{u}} - {b}_{\rm{l}}}}{2}g\left( {\left| {{u_{\rm{LQR}}} - {u_{\rm{SMC} }}} \right|} \right)\frac{{{u_{\rm{LQR}}} - {u_{\rm{SMC} }}}}{d}} \right) + {T_{\rm{d}}} $ (24)

式中：$c$为递减系数，该参数决定着舒适区、斥力区和吸引区的大小，公式内部的$c$有助于减少蝗虫之间的斥力或吸引力，外部的$c$随着迭代次数的增加，可减少对目标周围的搜索区域；$g\left( d \right)$为社会影响力，其为负数时表示相互排斥，为正数时表示相互吸引，计算方法如式（25）所示；${b}_{\rm{u}}$和${b}_{\rm{l}}$分别为$g\left( d \right)$的上、下界；$d{\text{ = }}\left| {{u_{\rm{LQR}}} - {u_{\rm{SMC} }}} \right|$，为蝗虫之间的距离；${T_{\rm{d}}}$为最优位置。

$ g\left( d \right) = f{{\rm e}^{\frac{{ - d}}{l}}} - {{\rm e}^{ - d}} $ (25)

式中：$f$为蝗虫间吸引强度；$l$为蝗虫间吸引力范围。蝗虫间的排斥力有助于蝗虫的全局搜索，而蝗虫间的吸引力则能保证蝗虫找到食物的目标位置。

利用式（26）更新参数$c$，并随着迭代次数的增加减少全局搜索，增加局部精度搜索，计算公式如下：

$ c = {c_{{\text{max}}}} - {L_{\rm{n}}}\frac{{{c_{{\text{max}}}} - {c_{{\text{min}}}}}}{L} $ (26)

式中：${c_{{\text{max}}}}$，${c_{{\text{min}}}}$分别为参数$c$的最大值和最小值；${L_{\rm{n}}}$为当前迭代次数；$L$为最大迭代次数。在整个搜索过程中，蝗虫位置的好坏由适应度函数$D = \psi - {\psi _{\text{d}}}$来判断，通过不断循环迭代寻找最优解，采用适应度函数计算得到的值为适应度值，迭代得到的最优适应度值即视为目前得到的最优解的值，得到的最优解的位置即为当前食物的目标位置${T_{\rm{d}}}$^[19]。

3 仿真分析

为了验证控制方法的正确性和有效性，本文以图3所示的中远集团COSCO SHANGHAI号船为对象进行仿真试验。该船的载货量为5 618 TEU，为巴拿马型集装箱船，其主要尺寸如下：船长280 m，船宽39.8 m，型深23.6 m，排水量69 500 t，平均吃水7.2 m；舵的展弦比为1.082，最大舵转角为20°。仿真中，大型船舶的状态变量$ {\boldsymbol{x}} = [ u\;\;v\;\;r\;\;x\;\;y\;\;\psi ] $，其初始值为：${u_0} = 6$ m/s，${v_0} = 0$，${r_0} = 0$，${x_0} = 0$，${y_0} = 0$，${\psi _0} = 0$。在3级海况下，有义波高${H_{\text{s}}}$ = 1.2 m，高频运动中的波浪强度系数$I$= 0.4 m，相对阻尼比$\lambda $= 0.26，波浪主导频率${w_{\text{o}}}$= 0.9 rad/s，非线性无源估计器的截止频率为1.0 rad/s。在5级海况下，${H_{\text{s}}}$ = 3.0 m，$I$= 0.9 m，$\lambda $= 0.26，${w_{\text{o}}}$= 0.6 rad/s，非线性无源估计器的截止频率为0.7 rad/s。

图 3. COSCO SHANGHAI large transport ship^[20]COSCO SHANGHAI号大型运输船^[20]

Fig. 3.

下载图片 查看所有图片

3.1 3级海况下3种控制方法的对比分析

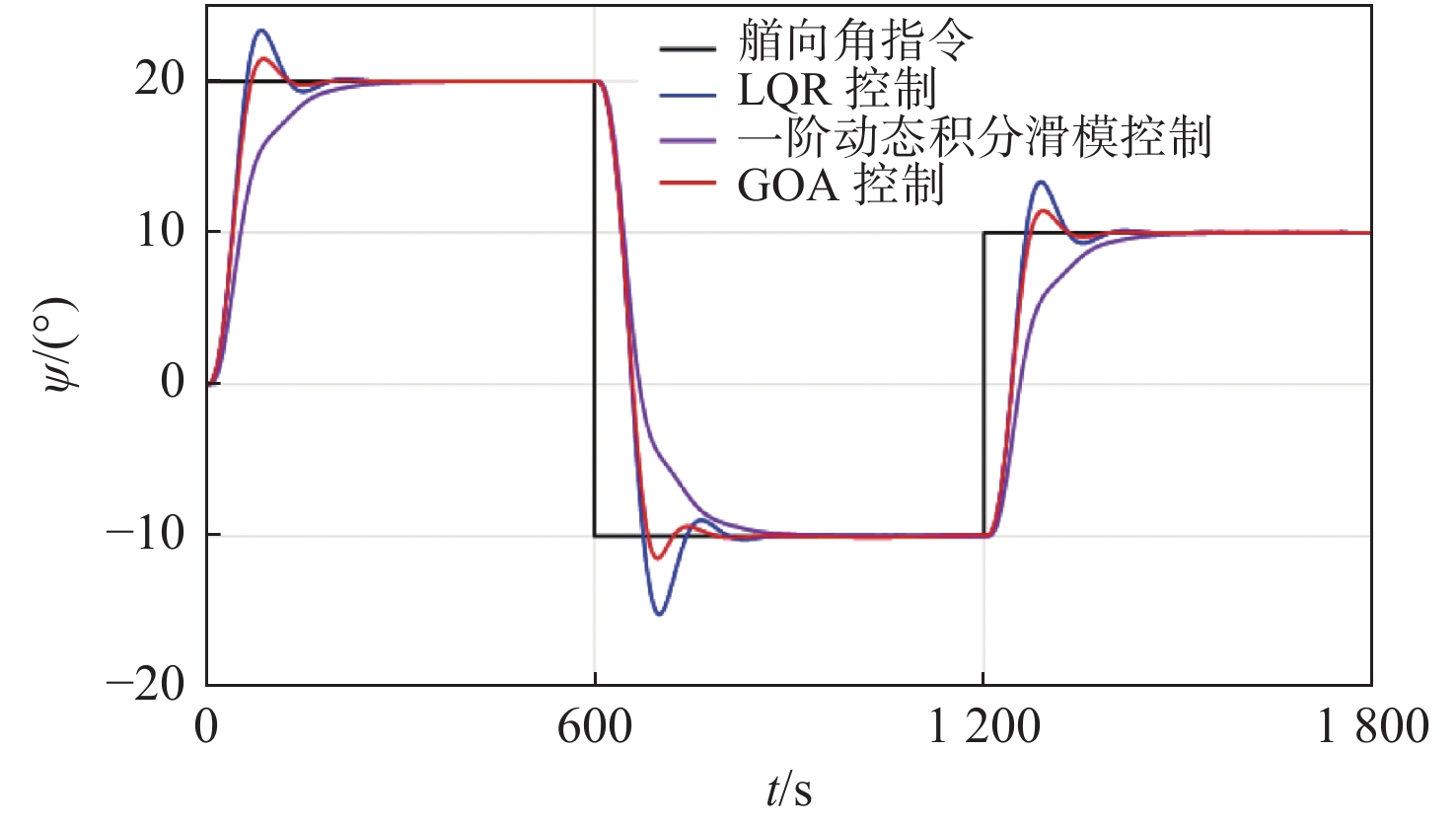
图4所示为在3级海况下，采用LQR控制、一阶动态积分滑模控制和GOA控制这3种控制方法控制的大型运输船舶模型的艏向角跟踪曲线。由图可见，艏向角的指令曲线是一条分段直线，大型运输船舶能自动沿着预定的艏向行驶，且实际的艏向角曲线接近于要求的直线，曲线光滑且无震荡。通过提高船舶跟踪误差的控制精度，可防止船舶出现偏航问题，提高了船舶航行的安全可靠性。

图 4. Curves of yaw angle tracking艏向角跟踪曲线

Fig. 4.

下载图片 查看所有图片

由表1所示的LQR控制方法与一阶动态积分滑模控制方法的对比可知，LQR控制系统的调整时间为158.4 s，无稳态误差，采用该种控制方法将具有更快的响应速度和更小的稳态误差，但超调量为33.48%，偏大；而一阶动态积分滑模控制系统的稳态误差为0.1°，超调量为2.12%，具有较强的鲁棒性，但调整时间为202.7 s，响应速度较慢。由图4所示的GOA控制曲线和表1中数据可知，相比LQR控制方法和一阶动态积分滑模控制方法，GOA控制方法具有两者的优点。该控制系统的调整时间为127.1 s，加快了响应速度，有12.16%的超调量，控制曲线光滑且无稳态误差，控制效果较好，其具有一阶动态积分滑模控制方法较小的超调量和强鲁棒性的特点，以及比LQR控制方法更快的响应速度和无稳态误差的优势。在外界干扰情况下，大型运输船舶兼顾鲁棒性和高精度艏向跟踪的要求具有一定的理论参考价值。

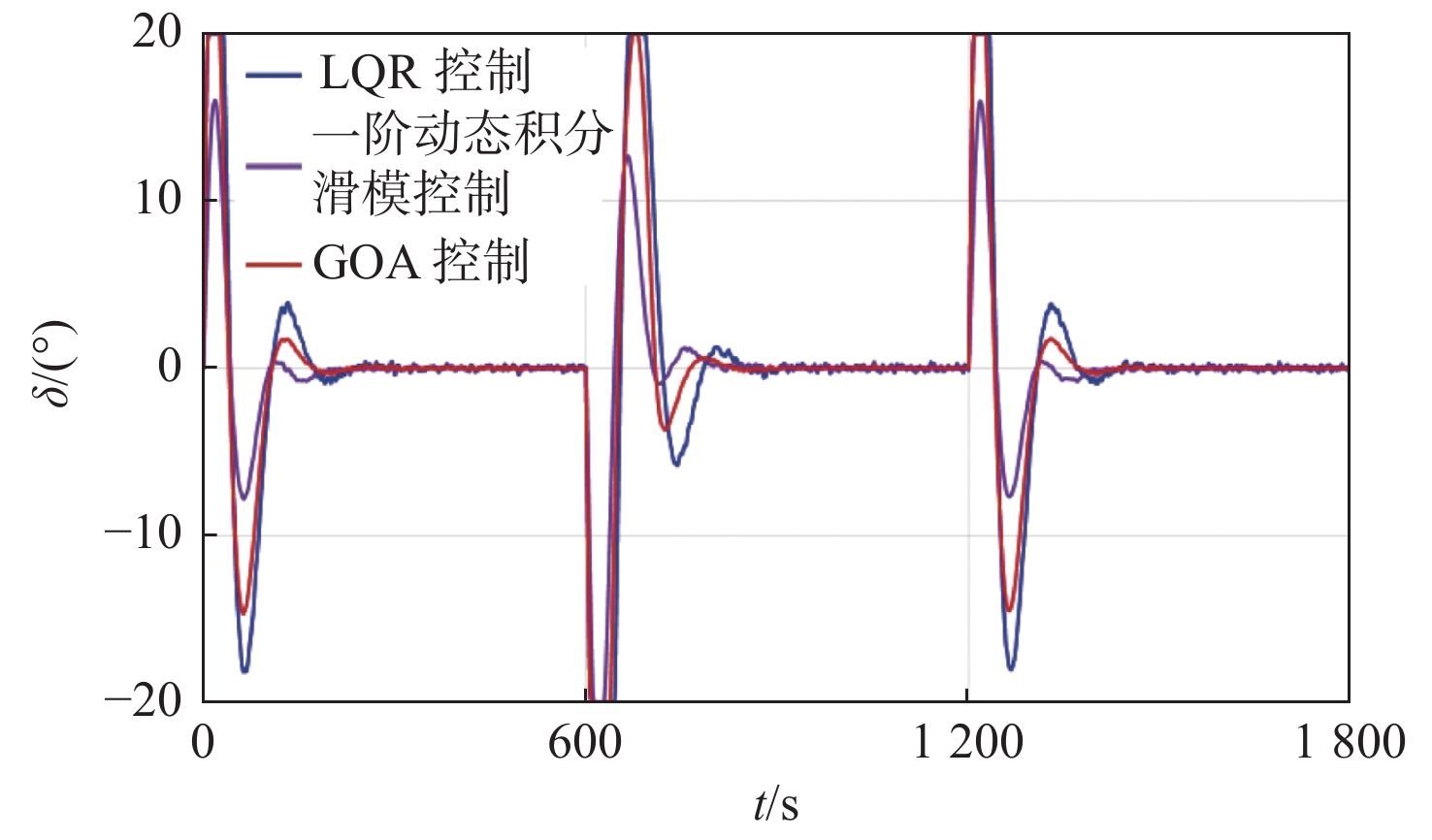
当船舶受到外力的作用而偏离原艏向一定角度时，舵角能及时纠正船舶的偏航，使艏向接近于要求的直线。图5所示为在3级海况下，采用3种控制方法控制的大型运输船舶模型的舵角响应曲线。由表1可知，LQR控制方法的操舵次数为193次，GOA控制方法的操舵次数为164次，比其降低了15%，从而保证了船舶的航行安全以及能耗的降低。总体来说，从稳定性、经济性、瞬态和稳态跟踪性能等多方面来考虑，GOA控制方法相对来说要稍好一些。

图 5. Response curves of rudder angle舵角响应曲线

Fig. 5.

下载图片 查看所有图片

3.2 不同海况下GOA控制方法的结果分析

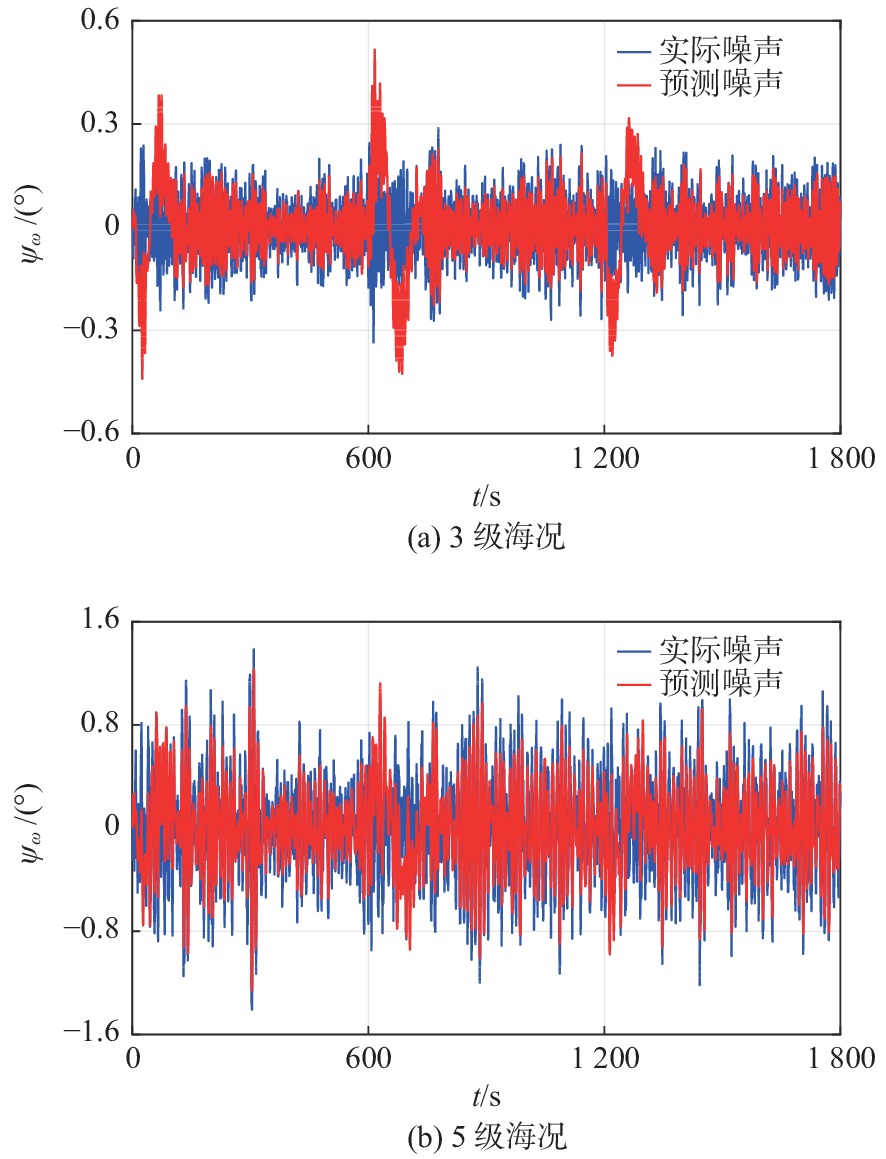
图6所示为转艏波浪扰动的预测曲线。由图可知，大型船舶在航行过程中受到的扰动影响较大，在3级海况下，实际噪声${\psi _\omega }$的最大值为0.3°，预测噪声${\hat \psi _\omega }$的最大值为0.52°；在5级海况下，实际噪声${\psi _\omega }$的最大值为1.39°，预测噪声${\hat \psi _\omega }$的最大值为1.23°，平均预测噪声均近乎为0，表明基于递推最小二乘法估计器的非线性无源估计器能够较为准确地估计出一阶波浪力的环境噪声。该估计器能够有效滤除由一阶波浪引起的高频成分，估算出船舶的艏向角状态，从而避免了频繁操舵，这对于减少舵机磨损和降低能耗具有重要意义^[21]。

图 6. Prediction curves of yaw wave disturbance转艏波浪扰动预测曲线

Fig. 6.

下载图片 查看所有图片

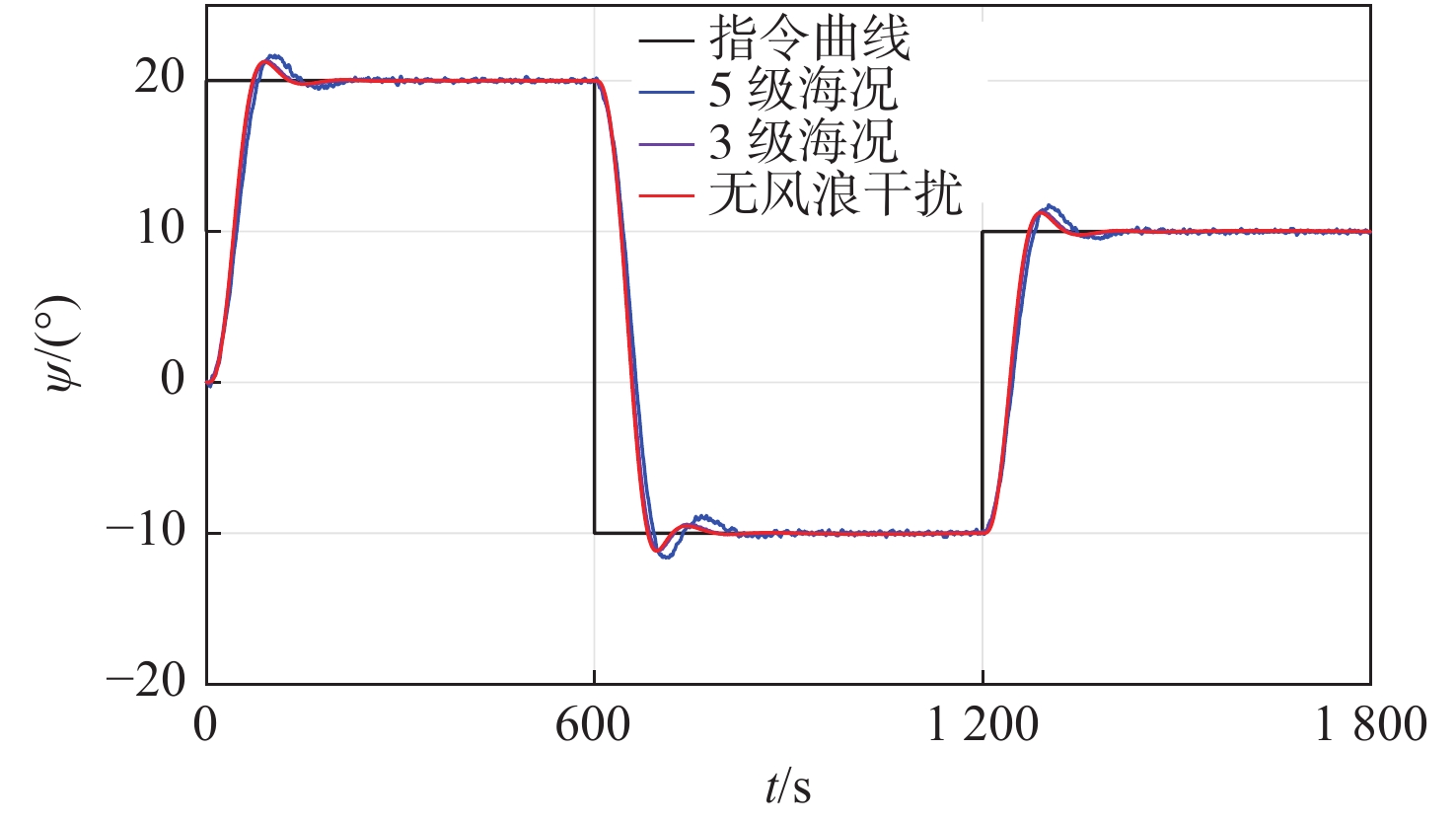
图7和图8所示分别为在5级和3级海况下以及无风浪干扰条件下，采用GOA控制方法的仿真结果对比图。由图7可知，在3级海况下，船舶实际艏向角跟踪曲线与无风浪干扰条件下的曲线几乎重合，表明在3级海况干扰下采用GOA控制方法对大型运输船舶的控制具有良好的稳定航行效果。在5级海况下，采用GOA控制方法时船舶实际艏向角跟踪曲线的超调量由3级海况下的12.16%上升到了16.47%，调节时间由127.1 s变为151.67 s，超调量和调整时间的变化均不大，在5级海况下无稳态误差，控制性能仍令人满意。在这2种海况下，控制器对船舶艏向控制得很好，说明采用GOA控制方法具有较强鲁棒性和高精度的控制性能，能够克服随机波浪的影响，适合智能船舶在外界干扰情况下的使用。

图 7. The yaw angle tracking curves of large transport ship controlled by GOA control method under different sea conditions不同海况下采用GOA控制方法控制的大型运输船舶的艏向角跟踪曲线

Fig. 7.

下载图片 查看所有图片

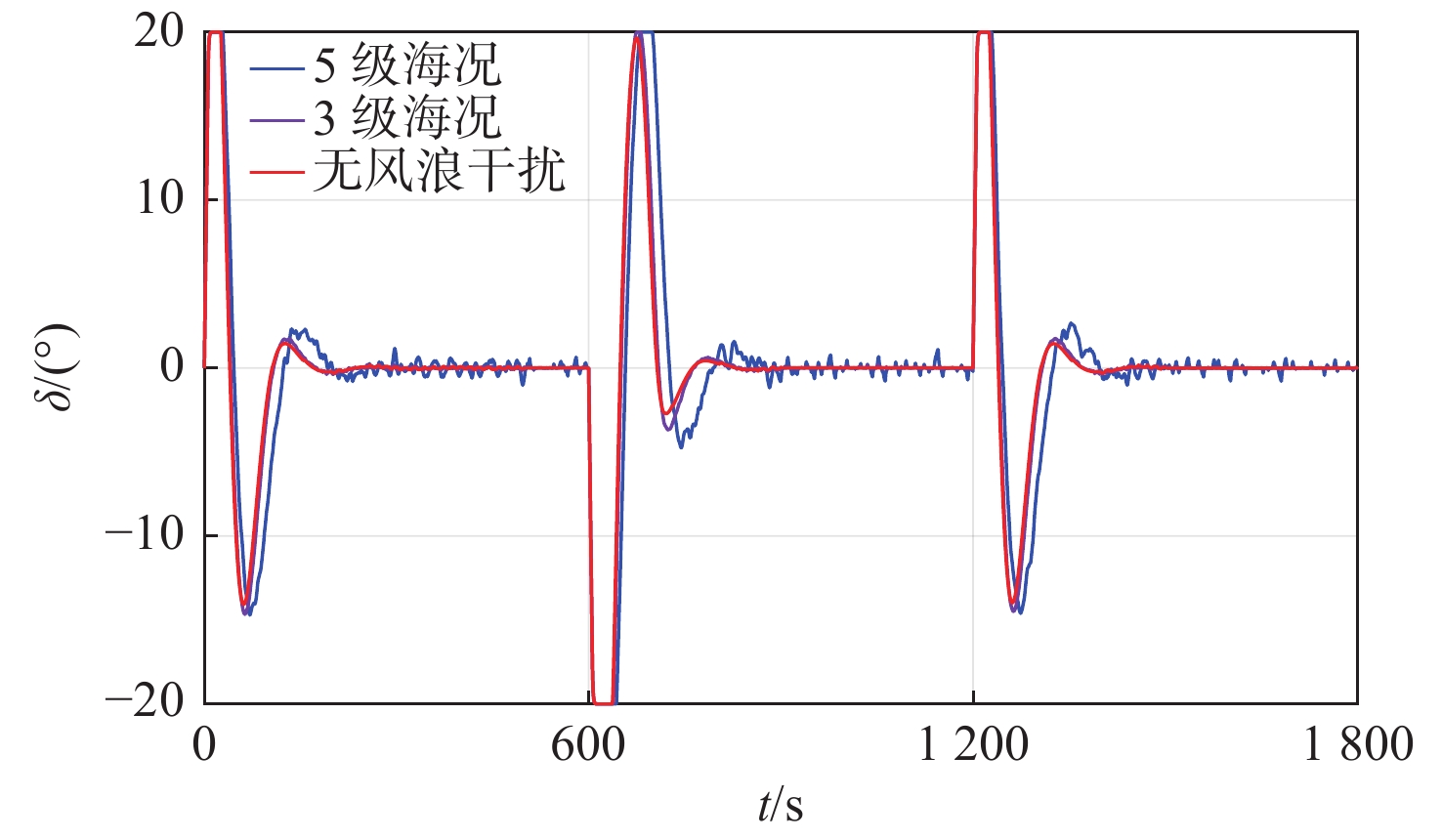
图 8. The rudder angle response curves of large transport ship controlled by GOA control method under different sea conditions不同海况下采用GOA控制方法控制的大型运输船舶的舵角响应曲线

Fig. 8.

下载图片 查看所有图片

由图8可见，在3级海况下，采用GOA控制方法控制的大型运输船舶的操舵次数为164次，在5级海况下的操舵次数为181次，随着海况级别由3级变为5级，操舵次数的变化不大，控制性能良好。在这2种海况下，控制器输出的操舵频率均较低，表明采用GOA控制方法能够降低对船舶的频繁操舵，具有一定的经济性。

4 结　语

本文提出了一种基于GOA的大型运输船舶自适应控制方法。文章通过在反馈控制中加入基于递推最小二乘法估计器的非线性无源估计器对大型运输船舶的运动状态进行实时估计，有效减少了频繁操舵次数，降低了能源消耗，提高了大型运输船舶的鲁棒性和经济性。仿真结果表明，在闭环仿真系统中，基于GOA的大型运输船舶自适应控制方法结合了LQR控制方法和一阶动态积分滑模控制方法的优点，具有更好的瞬态和稳态跟踪性能以及强鲁棒性，能对参数进行在线调节，增强了控制器的自适应特性。在不同海况下，采用该控制方法能够克服随机波浪的影响，具有较强的鲁棒性，可降低船舶频繁操舵的次数。可见，采用GOA控制方法能够极大地提高大型运输船舶航行的安全稳定性和控制精度，是一种有效、可行的控制方法。