非线性薛定谔方程的呼吸子解及其怪波极限

杜志峰; 宋丽军; 王艳

doi:doi:10.3788/LOP56.050601

激光与光电子学进展, 2019, 56 (5): 050601, 网络出版: 2019-07-31

非线性薛定谔方程的呼吸子解及其怪波极限下载： 1341次

Breather Solutions and Their Rouge Wave Limits of NonlinearSchrödinger Equation

论文大纲

杜志峰宋丽军 ^*王艳

作者单位

山西大学物理电子工程学院, 山西太原 030006

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

采用达布变换法得到了标准非线性薛定谔方程的一阶呼吸子解及其怪波极限,研究了一阶呼吸子解的动力学特性。借助达布变换的递推关系得到了非线性薛定谔方程的高阶呼吸子解,并分别研究了碰撞叠加、分离、简并和并行传输模式。当各呼吸子的频率趋于零时,得到非线性薛定谔方程怪波极限。研究结果表明,怪波幅值、凸起数以及怪波分裂后中心波峰的阶数和周围的波峰个数均与怪波阶数有关。

Abstract

Based on the standard nonlinear Schr dinger equation, the first-order breather solution and its rouge wave limit are obtained with Darboux transform method, and the dynamic characteristics of first-order breather solution are studied. High-order breather solutions of nonlinear Schr dinger equation are obtained by means of recurrence relation of Darboux transformation. And their collision superposition, separation, degeneracy and parallel transmission modes are studied, respectively. Nonlinear Schr dinger equation's rouge wave limit can be obtained when each breather frequency tends to zero. Research results show that the rouge wave's amplitude, number of bumps, order of center peaks and number of surrounding peaks after splitting are related to rouge wave's order.

1 引言

在现代科学与技术的发展过程中,系统的非线性特性一直受到广泛关注,非线性特性是理解很多自然现象的基础,在流体力学、化学、生物和非线性光学等领域均可以观察到,其重要性不容置疑。一般情况下,非线性现象利用线性和非线性效应的非线性演化方程进行建模,标准非线性薛定谔方程(NLSE)就是描述非线性现象的核心模型之一^[1-2]。

自20世纪60年代以来,非线性薛定谔方程已成为广泛研究的偏微分方程,一维自聚焦的非线性薛定谔方程被认为是描述海洋波的动力学模型^[3-10]。非线性薛定谔方程之所以被广泛研究,是因为其在海洋动力学之外的其他物理学分支中均有重要应用,如非线性光学^[11-12]、Bose-Einstein凝聚^[13]以及其他非线性物理学领域。NLSE的精确解包括孤子^[1]、Peregrine怪波(RW)^[14-15]、Akhmediev呼吸子(AB)^[16-17]、Kuznetsov-Ma孤子(KMS)^[18-19]以及这些解的不同组合^[20]。

目前,非线性薛定谔方程的呼吸子解被认为是在海洋以及其他物理领域中怪波的潜在原型^[21-23],当呼吸子周期趋于无穷大时,呼吸子解将成为有理分式的怪波解,因此,有关呼吸子的结果也将为怪波研究提供理论参考。1991年,呼吸子解首次被Kichenassamy^[24]求得;随后几十年,呼吸子解分别在非线性薛定谔方程^[25]、Korteweg-de Vries方程^[26-27]、二维Fermi-Pasta-Ulam晶格^[28]、向列相液晶盒^[29]和掺杂光纤^[14]等系统中获得;呼吸子由调制不稳定性(MI)^[14,30-31]导致的周期性扰动所产生,这些扰动通常是混沌的,可能在频谱中包含多个频率成份,因此,如何构建高阶解成为研究者非常关心的问题,Akhmediev小组认为高阶解可以是几个低阶解的非线性叠加^[32-33]。

在自然界中,怪波是一种突然出现但短时间内又突然消失并具有极强破坏力的波^[34],然而这种破坏性至今无法完全解释,航海家们一致认为线性理论无法解释怪波^[35],只有非线性理论才能解释这种能量集中且峰值幅度通常为有效波高两倍以上的现象。在最近的研究中,除NLSE方程之外,Hirota方程^[36]、Fokas-Leneels方程^[37]、Hirota Maxwell-Bloch(MB)方程^[38]、Sasa-Satsuma方程^[39]以及耗散系统^[40]中均已证明怪波的存在。经过研究,科学家们一致认为调制不稳定性是形成怪波最根本的动力学原因^[41],而高阶怪波是由具有相同或特定频率的多个呼吸子之间的相互作用形成^[42],即当两个或多个呼吸子碰撞时,会产生时空均局域且幅值较大的怪波^[43]。另外,对怪波形成机制的理解非常有用,在海洋中可以有效预防怪波的产生,从而避免造成危害;在光学领域的光纤系统中产生怪波,可以用于产生高能量脉冲。

本文基于标准非线性薛定谔方程,采用达布变换方法推导其一阶和高阶呼吸子的精确表达形式,并详细讨论怪波极限及其他动力学特性。

2 NLSE的一呼吸子解及其怪波极限

标准的无量纲NLSE的表达式为

\begin{matrix} i \frac{\partial ψ}{\partial x} + \frac{1}{2} \frac{\partial^{2} ψ}{\partial t^{2}} + {|ψ|}^{2} ψ = 0, (1) \end{matrix}

式中 $\begin{matrix} |ψ (x, t)| \end{matrix}$ 为脉冲包络,在光纤光学中^[21],x为沿光纤的传输距离,t为延迟时间。采用达布变换可以将NLSE的各阶呼吸解的递推表达式写成^[44]

\begin{matrix} ψ_{n} = ψ_{n - 1} + 2 (l_{n}^{*} - l_{n}) s_{n 1} r_{n 1}^{*} / ({|r_{n 1}|}^{2} + {|s_{n 1}|}^{2}), (2) \end{matrix}

式中n代表呼吸子解的阶数,l_n为复特征值,r_n₁和s_n₁为线性变化。

当n=1时,一阶呼吸子解为

\begin{matrix} ψ_{1} = ψ_{0} + 2 (l_{1}^{*} - l_{1}) s_{11} r_{11}^{*} / ({|r_{11}|}^{2} + {|s_{11}|}^{2}), (3) \end{matrix}

式中ψ₀=exp(ix)为种子解,复特征值l₁=a₁+ib₁,a₁为实部,b₁为虚部,调制频率与特征值的关系为κ_j=2 $\begin{matrix} \sqrt[]{1 + l_{j}^{2}} \end{matrix}$ =κ_j_r+iκ_j_i,下标r和i分别代表参数的实部与虚部,下标j表示n阶方程中第j个参数分量(1≤j≤n)。线性变化r₁₁、s₁₁的表达式见文献[ 44-45]附录。当a₁≠0且b₁≠0时,一呼吸子解如图1所示。特征值l₁的实部a₁控制呼吸子解的速度,虚部b₁控制呼吸子解的周期,当a₁=-0.5,b₁=0.8时,呼吸子的传输方向与t轴正向的夹角为锐角,在坐标平面内存在5个基本呼吸子周期,如图1(a)所示;当a₁=0.5,b₁=1时,呼吸子与t轴正向的夹角为钝角,且呼吸子的周期比图1(a)小,如图1(b)所示,图中色度条表示脉冲幅值 $\begin{matrix} |ψ| \end{matrix}$ 的大小(下文不再赘述)。

非线性薛定谔方程的呼吸子解及其怪波极限 下载： 1341次

1 引言

2 NLSE的一呼吸子解及其怪波极限

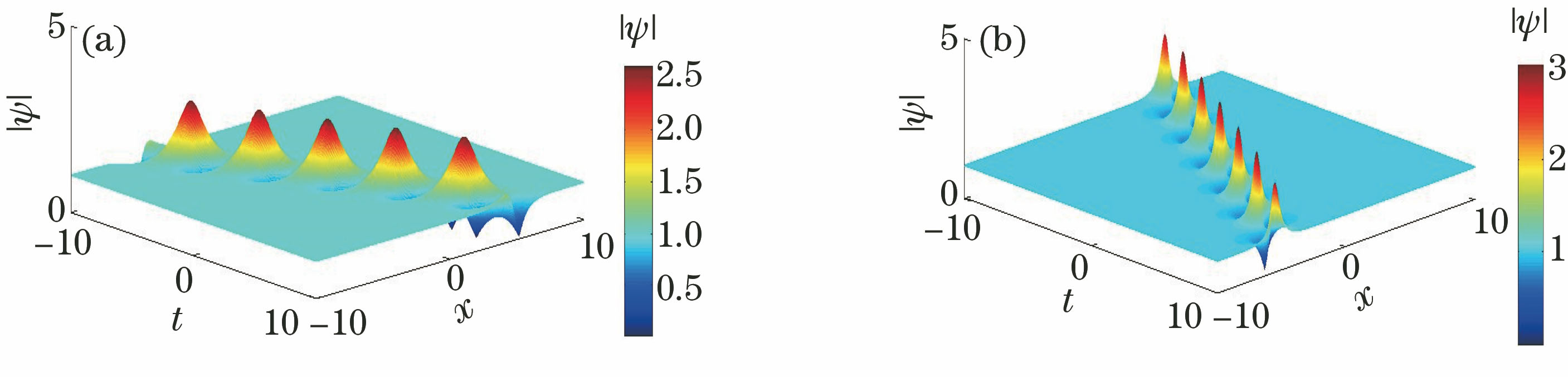
图 1. NLSE方程一呼吸子解。(a) a1=-0.5,b1=0.8;(b) a1=0.5,b1=1

Fig. 1. One-breather solution of NLSE. (a) a1=-0.5, b1=0.8; (b) a1=0.5, b1=1

图 2. Peregrine孤子解。(a) x1=0,t1=0;(b) x1=3,t1=3

Fig. 2. Peregrine soliton solution. (a) x1=0, t1=0; (b) x1=3, t1=3

3 NLSE的双呼吸子解及其怪波极限

图 3. 双呼吸子的碰撞。(a) b1=0.8;(b) b1→1;(c)双呼吸子碰撞的避免

Fig. 3. Collision of double breather. (a) b1=0.8; (b) b1→1; (c) avoid the collision of double breather

图 4. 呼吸子的碰撞与分离。(a)双AB碰撞;(b)双AB分离;(c) AB与KM孤子碰撞

Fig. 4. Collision and separation of breathers. (a) Double Akhmediev breather collision; (b) double Akhmediev breather separation; (c) collision between Akhmediev breather and Kuznetsov-Ma soliton

图 5. 二阶怪波的产生与分裂。(a)二阶怪波;(b)二维图;(c)分裂

Fig. 5. Generation and separation of second-order rouge waves. (a) Second-order rouge waves; (b) two-dimensional diagram; (c) separation

图 6. 双呼吸子碰撞。(a) κ1∶κ2=2κ∶κ; (b) κ1∶κ2=3κ∶2κ; (c) κ1∶κ2=4κ∶3κ

Fig. 6. Double breather collision. (a) κ1∶κ2=2κ∶κ; (b) κ1∶κ2=3κ∶2κ; (c) κ1∶κ2=4κ∶3κ

图 7. l1=-1.1705+1.4i,l2=-0.5+0.4i时双呼吸子的并行叠加。(a) x1=0,x2=0;(b)局部放大图;(c) x1=-2,x2=2

Fig. 7. Two breathers parallel superimposed with l1=-1.1705+1.4i and l2=-0.5+0.4i. (a) x1=0, x2=0; (b) partial enlargement; (c) x1=-2, x2=2

4 NLSE方程的三阶呼吸子解及其怪波极限

图 8. 三阶呼吸子的碰撞。(a)双重碰撞;(b)三重碰撞;(c)简并态

Fig. 8. Collisions of third-order breathers. (a) Double collision; (b) triple collision; (c) degeneration

图 9. 三阶怪波的产生与分裂。(a)三阶怪波;(b)等高图;(c)分裂

Fig. 9. Generation and separation of third-order rouge waves. (a) Third-order rouge waves; (b) contours; (c) separation

图 10. 三阶呼吸子的碰撞。(a) κ1∶κ2∶κ3=2∶3∶5且κ1=0.8;(b) κ1∶κ2∶κ3=2∶3∶5且κ1=0.6;(c) κ1∶κ2∶κ3=3∶2∶1且κ1=1.8

Fig. 10. Third-order breather collision. (a) κ1∶κ2∶κ3=2∶3∶5 and κ1=0.8; (b) κ1∶κ2∶κ3=2∶3∶5 and κ1=0.6; (c) κ1∶κ2∶κ3=3∶2∶1 and κ1=1.8

图 11. 三阶呼吸子的并行传输。(a) x1=0,x2=0,x3=0;(b)局部放大图;(c) x1=-4,x2=0,x3=4

Fig. 11. Third-order breather parallel transmission. (a) x1=0, x2=0, x3=0; (b) partial enlargement; (c) x1=-4, x2=0, x3=4

5 NLSE的四阶呼吸子解及其怪波极限

图 12. 四阶呼吸子的相互作用。(a)双重碰撞;(b)四重碰撞

Fig. 12. Fourth-order breather interaction. (a) Double collision; (b) fourfold collision

图 13. 呼吸子的简并。(a) AB简并与KM孤子简并叠加;(b) AB的简并

Fig. 13. Degenerate breather. (a) Superposition of Akhmediev breather and Kuznetsov-Ma soliton degenerate state; (b) degenerate Akhmediev breather

图 14. 四阶怪波的产生。(a)四阶怪波;(b)二维图;(c)等高图

Fig. 14. Generation of fourth-order rouge wave. (a) Fourth-order rouge waves; (b) two-dimensional diagram; (c) contour map

图 15. 四阶怪波的分裂。(a)一次分裂;(b)两次分裂

Fig. 15. Separation of fourth-order rouge wave. (a) Once separation; (b) twice separation

图 16. 四阶呼吸子相互作用的等高图。(a) κ1∶κ2∶κ3∶κ4=1∶3∶5∶7;(b) κ1∶κ2∶κ3∶κ4=2∶4∶6∶8

Fig. 16. Contour map of fourth-order breather interaction. (a) κ1∶κ2∶κ3∶κ4=1∶3∶5∶7; (b) κ1∶κ2∶κ3∶κ4=2∶4∶6∶8

图 17. 四阶呼吸子的并行传输。(a) x1=0,x2=0,x3=0,x4=0;(b)局部放大图;(c) x1=-6,x2=-2,x3=2,x4=6

Fig. 17. Third-order breather parallel transmission. (a) x1=0, x2=0, x3=0, x4=0; (b) partial enlargement; (c) x1=-6, x2=-2, x3=2, x4=6

6 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

非线性薛定谔方程的呼吸子解及其怪波极限下载： 1341次