(2+1)维色散长波方程的新孤子解及其演化

杨娟; 冯庆江

doi:doi:10.3788/LOP55.011901

激光与光电子学进展, 2018, 55 (1): 011901, 网络出版: 2018-09-10

(2+1)维色散长波方程的新孤子解及其演化下载： 1132次

New Soliton Solutions and Soliton Evolvements for (2+1)-Dimensional Dispersive Long Wave Equation

论文大纲

杨娟 ^*冯庆江

作者单位

凯里学院理学院, 贵州凯里 556000

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

借助Mathematica数学软件进行符号计算,先将由G''/G展开法改进得到的F/G展开法进行拓展,然后结合变量分离法得到一系列高维非线性发展方程的精确解。以(2+1)维色散长波方程为例,利用F/G展开法构造精确解的方法是将原来的行波变换扩展为任意函数的变换,行波变换则成为任意函数变换的特例,从而得到(2+1)维色散长波方程的非行波解。通过选择适当的函数,分别构造出(2+1)维色散长波方程的亮暗dromion解(局域解)和周期孤立波解。研究了设定参数下亮暗dromion解随时间的传播情况,以及周期孤立波解随时间的演化情况。

Abstract

With the help of Mathematica symbol calculation software, we extend the F/G expansion method improved by the G''/G expansion method and obtain exact solutions of a series of high dimensional nonlinear evolution equations by combining the variable separation method. Taking a (2+1)-dimensional dispersive long wave equation as an example, constructing the exact solutions by F/G expansion method is to extend the original traveling wave transform to any function transform, in which the traveling wave transform is only a special case of this any function transform. Then the non-traveling wave solutions of the (2+1)-dimensional dispersive long wave equation are obtained. By choosing the appropriate function, we can construct (2+1)-dimensional bright dromion solution and periodic solitary wave solution of the dispersion long wave equation. Then we study the propagation of the bright dromion solution with time and the evolution of the periodic solitary wave solution over time further.

1 引言

孤立子理论是非线性科学中重要的研究方向之一,在数学、物理学、计算机、生物、天文学等自然科学中的许多领域有着广泛的应用,如生物系统、气体动力学、流体力学、凝聚态物理、等离子体物理、非线性光学、光纤通信、海上冲击波、涡旋星系的密度波等领域。在孤立子理论的研究过程中,出现了许多求解非线性发展方程的好方法,比如Painleve分析法^[1]、三波测试方法^[2]、同宿测试法^[3]、双线性导数法^[4]、简单方程法^[5]、试探函数法^[6]、tanh-coth展开法^[7]、齐次平衡法^[8]、行波约化法^[9]、Adomian分解法^[10]、Jacobi椭圆函数法^[11]、F-函数扩展法^[12]、分步傅里叶法^[13]、相似变换法^[14]、变分法^[15-17]、拟解法^[18]、分离变量法^[19]等,使用这些方法均可成功地求解不同类型的非线性发展方程。

洪宝剑等^[20]在研究水波运动的过程中,提出了著名的非线性色散长波方程

\begin{matrix} \{\begin{matrix} u_{ty} + v_{xx} + {(u^{2})}_{xy} / 2 = 0 \\ v_{t} + {(uv + u + β^{2} u_{xy})}_{x} = 0 \end{matrix}, (1) \end{matrix}

式中u(x,y,t)、v(x,y,t)为所示变量的物理场,x、y代表空间坐标,t代表时间,β为参数,该方程是描述水波通过等深、狭长理想运动水道的重要方程。当x=y且β²=1时约化为经典的Boussinesq方程

\begin{matrix} u_{ty} + v_{xx} + {(u^{2})}_{xy} / 2 = 0, (2) \end{matrix}

当β²=1时约化为通常的(2+1)维非线性色散长波方程

\begin{matrix} v_{t} + u_{x} + {(uv)}_{x} + u_{xxy} = 0, (3) \end{matrix}

这是Boiti等^[21]在研究弱Lax对的相容条件时得到的。经过几十年的不断努力,众多学者获得了(2+1)维非线性色散长波方程^[22-27]不同类型的孤子解。本文利用拓展的F/G展开法^[28]求解(2+1)维非线性色散长波方程,获得新的精确解,并研究了孤子解的结构和性质。

2 (2+1)维色散长波方程的精确解

对于给定的一个非线性物理模型

\begin{matrix} P (u, u_{t}, u_{x}, u_{y}, u_{tt}, u_{xx}, u_{yy}, u_{tx}, u_{ty}, u_{xy}, \dots) = 0, (4) \end{matrix}

设它的解为

\begin{matrix} u (ξ) = a_{0} + \overset{m}{\sum_{i = 1}} a_{i} {(F / G)}^{i}, (5) \end{matrix}

式中G=G(ξ),F=F(ξ)满足一阶线性常系数微分方程

\begin{matrix} F' (ξ) = λG (ξ), G' (ξ) = μF (ξ), (6) \end{matrix}

式中F'(ξ)= $\begin{matrix} \frac{dF (ξ)}{dξ} \end{matrix}$ ,G'(ξ)= $\begin{matrix} \frac{dG (ξ)}{dξ} \end{matrix}$ ,ξ=x+y-Vt为行波变换,V为常数。然后将假设解(5)式代入(4)式,应用齐次平衡法可以得到(5)式的行波解。根据(6)式可以得到

\begin{matrix} \begin{matrix} \{\begin{matrix} F (ξ) = C_{1} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} (\sqrt[]{λ} / \sqrt[]{μ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ), \\ G (ξ) = C_{1} (\sqrt[]{μ} / \sqrt[]{λ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ), \end{matrix} λ > 0, μ > 0, (7) \\ \{\begin{matrix} F (ξ) = C_{1} \cos h (\sqrt[]{- λ} \sqrt[]{- μ} ξ) - C_{2} (\sqrt[]{- λ} / \sqrt[]{- μ}) \sin h (\sqrt[]{- λ} \sqrt[]{- μ} ξ), \\ G (ξ) = - C_{1} (\sqrt[]{- μ} / \sqrt[]{- λ}) \sin h (\sqrt[]{- λ} \sqrt[]{- μ} ξ) + C_{2} \cos h (\sqrt[]{- λ} \sqrt[]{- μ} ξ), \end{matrix} λ < 0, μ < 0, (8) \\ \{\begin{matrix} F (ξ) = C_{1} \cos (\sqrt[]{λ} \sqrt[]{- μ} ξ) + C_{2} (\sqrt[]{λ} / \sqrt[]{- μ}) \sin (\sqrt[]{λ} \sqrt[]{- μ} ξ), \\ G (ξ) = - C_{1} (\sqrt[]{- μ} / \sqrt[]{λ}) \sin (\sqrt[]{λ} \sqrt[]{- μ} ξ) + C_{2} \cos (\sqrt[]{λ} \sqrt[]{- μ} ξ), \end{matrix} λ > 0, μ < 0, (9) \\ \{\begin{matrix} F (ξ) = C_{1} \cos (\sqrt[]{- λ} \sqrt[]{μ} ξ) - C_{2} (\sqrt[]{- λ} / \sqrt[]{μ}) \sin (\sqrt[]{- λ} \sqrt[]{μ} ξ), \\ G (ξ) = C_{1} (\sqrt[]{μ} / \sqrt[]{- λ}) \sin (\sqrt[]{- λ} \sqrt[]{μ} ξ) + C_{2} \cos (\sqrt[]{- λ} \sqrt[]{μ} ξ), \end{matrix} λ < 0, μ > 0 。 (10) \end{matrix} \end{matrix}

利用F/G展开法构造高维非线性方程的精确解的方法是:将原来的行波变换ξ=x+y-Vt扩展为任意函数ξ=ξ(x,y,t)变换,而行波变换ξ=x+y-Vt仅为这个任意函数的特例。那么,当ξ为任意函数时得到的解称为非行波解。

下面求(2+1)维色散长波方程的非行波解。根据齐次平衡原则,可以假设

\begin{matrix} \begin{matrix} u = a_{0} (x, y, t) + a_{1} (x, y, t) F (ξ) / G (ξ), (11) \\ v = b_{0} (x, y, t) + b_{1} (x, y, t) F (ξ) / G (ξ) + b_{2} (x, y, t) F^{2} (ξ) / G^{2} (ξ), (12) \end{matrix} \end{matrix}

式中ξ=f(x,t)+g(y)。将(11)、(12)式代入(2)、(3)式,并按F/G的同次幂合并,提取 $\begin{matrix} {(\frac{F}{G})}^{i} \end{matrix}$ (i=1,2,…)前的系数,令其等于零,得到一系列的方程。由这些方程可以求得

\begin{matrix} \begin{matrix} a_{0} = - (f_{t} + f_{xx}) / f_{x}, a_{1} = 2 μ f_{x}, b_{0} = - 1 + 2 λμ f_{x} g_{y}, b_{1} = 0, b_{2} = - 2 μ^{2} f_{x} g_{y}, (13) \\ a_{0} = - (f_{t} - f_{xx}) / f_{x}, a_{1} = - 2 μ f_{x}, b_{0} = - 1 + 2 λμ f_{x} g_{y}, b_{1} = 0, b_{2} = - 2 μ^{2} f_{x} g_{y}, (14) \end{matrix} \end{matrix}

将(13)式代入(11)、(12)式,根据(7)式,就可以得到(2+1)维色散长波方程的孤立波解

\begin{matrix} \begin{matrix} u = (- \frac{f_{t} + f_{xx}}{f_{x}}) + 2 μ f_{x} [\frac{C_{1} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} (\sqrt[]{λ} / \sqrt[]{μ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ)}{C_{1} (\sqrt[]{μ} / \sqrt[]{λ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ)}], (15) \\ v = (- 1 + 2 λμ f_{x} g_{y}) - 2 μ^{2} f_{x} g_{y} {[\frac{C_{1} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} (\sqrt[]{λ} / \sqrt[]{μ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ)}{C_{1} (\sqrt[]{μ} / \sqrt[]{λ}) \sin h (\sqrt[]{λ} \sqrt[]{μ} ξ) + C_{2} \cos h (\sqrt[]{λ} \sqrt[]{μ} ξ)}]}^{2}, (16) \end{matrix} \end{matrix}

式中ξ=f(x,t)+g(y)。对于其他几组解,这里不再分别给出其具体形式。

3 孤子随时间的演化

由于(15)、(16)式都含有任意函数f(x,t)和g(y),解的类型变得更加丰富,数量增多。以(16)式为例,研究(2+1)维色散长波方程的孤子结构。

3.1 传播孤子

在(16)式中,如果取

\begin{matrix} \{\begin{matrix} f (x, t) = 1 + \sec h^{2} (x + ct) \\ g (y) = \tan h (ky) \end{matrix}, (17) \end{matrix}

当参数分别为λ=1,μ=1,C₁=1,C₂=1,k=1,c=1,时间t为-1 ,0,1 s时,可以得到如图1所示的亮暗dromion孤波解。

根据图1可以清晰地看到,随时间t的增加,亮暗dromion孤子的传播速度v、波幅和波形都保持不变,孤子沿x轴负方向移动。

3.2 湮灭孤子

在(16)式中,如果取

\begin{matrix} \{\begin{matrix} f (x, t) = \sec h (x^{2} + t) \\ g (y) = \cos (ky) \end{matrix}, (18) \end{matrix}

当参数分别为λ=1,μ=1,C₁=1,C₂=1,k=1,时间t为-1.5,0,0.5,1.0,1.5,3.0 s时得到如图2所示的周期孤立波解。

从图2可以看到,由于他们都是亮暗dromion周期孤子,亮孤子和暗孤子的波幅、大小和形状完全一样,随着时间t的不断增加,两列波叠加后波幅逐渐变为零,最后两个孤子消失。

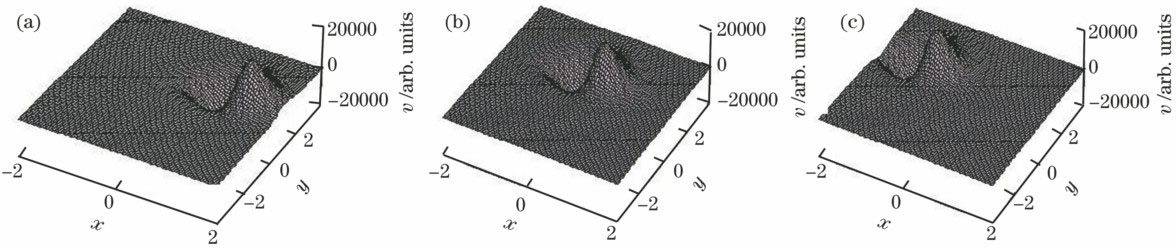
图 1. (17)式代入(16)式得到的传播孤子。(a) t=-1 s;(b) t=0 s;(c) t=1 s

Fig. 1. Propagation soliton obtained from Eq.(16) based on Eq.(17). (a) t=-1 s; (b) t=0 s; (c) t=1 s

下载图片查看所有图片

图 2. (17)式代入(15)式得到的湮灭孤子。(a) t=-1.5 s;(b) t=0 s;(c) t=0.5 s;(d) t=1.0 s;(e) t=1.5 s;(f) t=3.0 s

Fig. 2. Annihilation soliton obtained from Eq.(15) based on Eq.(17). (a) t=-1.5 s; (b) t=0 s; (c) t=0.5 s; (d) t=1.0 s; (e) t=1.5 s; (f) t=3.0 s

下载图片查看所有图片

4 结论

利用拓展的F/G展开法和变量分离法,得到了(2+1)维色散长波方程的精确解,这里与文献[ 22-27]中得到的精确解有所不同。通过选择两个适当的函数,构造出(2+1)维色散长波方程的亮暗dromion解和周期孤立波解,研究了亮暗dromion孤子在水平方向随时间的传播情况,以及周期孤子在垂直方向随时间的湮灭情况。实践证明,拓展的F/G展开法可简便、有效地求解非线性方程,但用于求解其他高维非线性物理模型还有待于进一步研究。

参考文献

[1] 谭伟, 戴正德. 2+1)维Broer-Kaup-Kupershmidt方程的新局域结构[J]. 应用数学与计算数学学报, 2016, 30(3): 421-428.

Tan W, Dai Z D. New localized structures for (2+1)-dimensional Broer-Kaup-Kupershmidt eqution[J]. Communication on Applied Mathematics and Computation, 2016, 30(3): 421-428.

[2] 许镇辉, 陈翰林, 戴正德. 2+1)维Kadomtsev-Petviashvili方程解的时空分岔[J]. 应用数学学报, 2013, 36(5): 900-909.

Xu Z H, Chen H L, Dai Z D. Spatiotemporal bifurcation of soliton for the (2+1)-dimensional Kadomtsev-Petviashvili equation for recurrent event data[J]. Acta Mathematicae Applicatae Sinica, 2013, 36(5): 900-909.

[3] 陈炜, 杜先云. 拓展的2+1维Sine-Gordon方程的周期孤立波解[J]. 西南师范大学学报(自然科学版), 2012, 37(7): 33-36.

Chen W, Du X Y. Periodic solitary solution for the (2+1)-dimensional extension of the Sine-Gordon equation[J]. Journal of Southeast China Normal University (Natural Science Edition), 2012, 37(7): 33-36.

[4] Lü X, Lin F. Soliton excitations and shape-changing collisions in alpha helical proteins with interspine coupling at higher order[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 32: 241-261.

[5] 杨娟, 冯庆江. 应用改进的简单方程法求(2+1)维ZK-MEW方程的精确解[J]. 量子电子学报, 2016, 33(3): 287-291.

Yang J, Feng Q J. Exact solutions for (2+1)-dimensional ZK-MEW equation with modified simple equation method[J]. Chinese Journal of Quantum Electronics, 2016, 33(3): 287-291.

[6] 杨娟, 冯庆江. 应用改进的试探函数法求非线性数学物理方程的精确解[J]. 量子电子学报, 2016, 33(4): 444-450.

Yang J, Feng Q J. Exact solutions of nonlinear mathematical physics equations with improved trial function method[J]. Chinese Journal of Quantum Electronics, 2016, 33(4): 444-450.

[7] 郭鹏, 陈宗广, 孙小伟. 非线性电报方程的简洁解法[J]. 大学物理, 2014, 33(4): 15-17.

Guo P, Chen Z G, Sun X W. A simple approach for solving nonlinear telegraph equation[J]. College Physics, 2014, 33(4): 15-17.

[8] 白成林, 徐炳振, 刘希强. 高阶Broer-Kaup(BK)方程组的新精确解[J]. 光子学报, 1999, 28(5): 431-435.

Bai C L, Xu B Z, Liu X Q. Some new and exact explicit solutions of the higher order Broer-Kaup systems[J]. Acta Photonica Sinica, 1999, 28(5): 431-435.

[9] 马松华, 朱加民. 含高阶非线性效应的薛定谔方程的精确解研究[J]. 量子光学学报, 2006, 12(3): 156-158.

Ma S H, Zhu J M. The exact wave solutions of higher-order nonlinear Schrödinger equation[J]. Acta Sinica Quantum Optica, 2006, 12(3): 156-158.

[10] 刘燕, 张素英. 横向非周期调制的五次非线性薛定谔方程的精确孤子解[J]. 量子光学学报, 2015, 21(2): 153-159.

Liu Y, Zhang S Y. Exact soliton solution for quintic-nonlinear Schrödinger equation with a type of transverse nonperiodic modulation[J]. Journal of Quantum Optics, 2015, 21(2): 153-159.

[11] 员保云, 庞晶. 求解非线性薛定谔方程的几种方法[J]. 激光与光电子学进展, 2014, 51(4): 040604.

Yuan B Y, Pang J. Several methods for solving nonlinear Schrödinger equation[J]. Laser & Optoelectronics Progress, 2014, 51(4): 040604.

[12] 庄彬先, 郭珺, 项元江, 等. F-函数扩展法求解超介质中的亮孤子和暗孤子[J]. 物理学报, 2013, 62(5): 054207.

Zhuang B X, Guo J, Xiang Y J, et al. Bright and dark solitons in metamaterials obtained by extended F-expansion method[J]. Acta Physica Sinica, 2013, 62(5): 054207.

[13] 武达, 王娟芬, 石佳, 等. 掺杂光纤中peregrine孤子的产生和传输[J]. 光学学报, 2017, 37(4): 0406002.

Wu D, Wang J F, Shi J, et al. Generation and transmission of peregrine soliton in doped fiber[J]. Acta Optica Sinica, 2017, 37(4): 0406002.

[14] 张解放, 赵辟, 胡文成, 等. 非均匀非线性波导中涡旋光孤子的相互作用传播[J]. 光学学报, 2013, 33(4): 0419001.

Zhang J F, Zhao B, Hu W C, et al. Interaction propagation of optical vortex solitons in inhomogeneous nonlinear waveguides[J]. Acta Optica Sinica, 2013, 33(4): 0419001.

[15] 王清, 王形华, 谢应茂, 等. 非局域椭圆厄米-高斯空间光孤子与相移[J]. 激光与光电子学进展, 2012, 49(2): 021901.

Wang Q, Wang X H, Xie Y M, et al. Elliptical Hermite-Gaussian spatial optical soliton and phase shift[J]. Laser & Optoelectronics Progress, 2012, 49(2): 021901.

[16] 白东峰, 卢宏炎. 强非局域非线性介质中1+1维厄米-高斯损耗光孤子[J]. 量子电子学报, 2016, 33(5): 584-589.

Bai D F, Lu H Y. 1+1 dimension Hermite-Gauss lossy solitons in strongly nonlocal nonlinear media[J]. Chinese Journal of Quantum Electronics, 2016, 33(5): 584-589.

[17] 周博臻, 花春波, 徐四六, 等. PT对称晶格势中涡旋光孤子[J]. 中国激光, 2015, 42(5): 0505004.

Zhou B Z, Hua C B, Xu S L, et al. Optical vortex soliton in parity-time symmetric potentials[J]. Chinese Journal of Lasers, 2015, 42(5): 0505004.

[18] 陈昶, 周文龙, 宋丽军. 基于耦合Ginzburg-Landau方程的石墨烯锁模光纤激光器的暗暗孤子解及其稳定性[J]. 量子光学学报, 2015, 21(2): 160-164.

Chen C, Zhou W L, Song L J. Ultra-short dark soliton pair and their stabilities of graphene mode-locked fiber lasers based on coupled Ginzburg-Landau equationg[J]. Journal of Quantum Optics, 2015, 21(2): 160-164.

[19] 刘飞, 李金星. 系统参数对势阱调制下的空间光孤子分布的影响[J]. 光电子·激光, 2016, 27(5): 566-572.

Liu F, Li J X. Effect of parameters on spatial solitons modulated by two-dimensional infinite potential trap[J]. Journal of Optoelectronic·Laser, 2016, 27(5): 566-572.

[20] 洪宝剑, 方国昌, 卢殿臣, 等. 2+1)维色散长波方程新的类孤子解[J]. 数学的实践与认识, 2009, 39(1): 194-197.

Hong B J, Fang G C, Lu D C, et al. New soliton-like solutions to the (2+1)-dimensional dispersive long wave equations[J]. Mathematics in Practice and Theory, 2009, 39(1): 194-197.

[21] Boiti P. Leon J J P, Manna M, et al. On a spectral transform of a KdV-like equation related to the Schrödinger operator in the plane[J]. Inverse Problems, 1987, 3(1): 25-36.

[22] Qawasmeh A, Alquran M. Soliton and periodic solutions for (2+1)-dimensional dispersive long water-wave system[J]. Applied Mathematical Sciences, 2014, 8(50): 2455-2463.

[23] HuJ, Xu ZW, Yu GF. Determinant structure for the (2+1)-dimensional dispersive long wave system[J]. Applied Mathematics Letters, 2016( 62): 76- 83.

[24] Xia Y R, Xin P X, Zhang S L. Residual symmetry, interaction solutions, and conservation laws of the (2+1)-dimensional dispersive long-wave system[J]. Chinese Physics B, 2017, 26(3): 0302021.

[25] 卢殿臣, 杨广娟. 2+1)维非线性色散长波方程新的类孤子解和局域相干结构[J]. 应用数学, 2007, 20(4): 777-782.

Lu D C, Yang G J. New solitons-like solutions and localized coherent structures to the (2+1)-dimensional dispersive long wave equations with variable coefficients[J]. Mathematica Applicata, 2007, 20(4): 777-782.

[26] 章超艳, 李彪. 2+1)维色散长波方程的非局域对称及相容Riccati展开可积性[J]. 应用数学与计算数学学报, 2016, 30(4): 618-626.

Zhang C Y, Li B. Nonlocal symmetries and consistent riccati expansion integrability of (2+1)-dimensional dispersive long-wave equations[J]. Communication on Applied Mathematics and Computation, 2016, 30(4): 618-626.

[27] 林福忠, 马松华. 2+1)维色散长波方程的新精确解及其复合波激发[J]. 物理学报, 2014, 63(4): 040508.

Lin F Z, Ma S H. New exact solutions and complex wave excitations for the (2+1)-dimensional dispersive long wave equation[J]. Acta Physica Sinica, 2014, 63(4): 040508.

[28] Lee Y, An J H. New exact solutions of some nonlinear evolution equations by Sub-ODE method[J]. Honam Mathematical Journal, 2013, 35(4): 683-699.

杨娟, 冯庆江. (2+1)维色散长波方程的新孤子解及其演化[J]. 激光与光电子学进展, 2018, 55(1): 011901. Yang Juan, Feng Qingjiang. New Soliton Solutions and Soliton Evolvements for (2+1)-Dimensional Dispersive Long Wave Equation[J]. Laser & Optoelectronics Progress, 2018, 55(1): 011901.

(2+1)维色散长波方程的新孤子解及其演化下载： 1132次

1 引言

2 (2+1)维色散长波方程的精确解

3 孤子随时间的演化

3.1 传播孤子

3.2 湮灭孤子

图 1. (17)式代入(16)式得到的传播孤子。(a) t=-1 s;(b) t=0 s;(c) t=1 s

Fig. 1. Propagation soliton obtained from Eq.(16) based on Eq.(17). (a) t=-1 s; (b) t=0 s; (c) t=1 s

图 2. (17)式代入(15)式得到的湮灭孤子。(a) t=-1.5 s;(b) t=0 s;(c) t=0.5 s;(d) t=1.0 s;(e) t=1.5 s;(f) t=3.0 s

Fig. 2. Annihilation soliton obtained from Eq.(15) based on Eq.(17). (a) t=-1.5 s; (b) t=0 s; (c) t=0.5 s; (d) t=1.0 s; (e) t=1.5 s; (f) t=3.0 s

4 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

(2+1)维色散长波方程的新孤子解及其演化 下载： 1132次

1 引言

2 (2+1)维色散长波方程的精确解

3 孤子随时间的演化

3.1 传播孤子

3.2 湮灭孤子

图 1. (17)式代入(16)式得到的传播孤子。(a) t=-1 s;(b) t=0 s;(c) t=1 s

Fig. 1. Propagation soliton obtained from Eq.(16) based on Eq.(17). (a) t=-1 s; (b) t=0 s; (c) t=1 s

图 2. (17)式代入(15)式得到的湮灭孤子。(a) t=-1.5 s;(b) t=0 s;(c) t=0.5 s;(d) t=1.0 s;(e) t=1.5 s;(f) t=3.0 s

Fig. 2. Annihilation soliton obtained from Eq.(15) based on Eq.(17). (a) t=-1.5 s; (b) t=0 s; (c) t=0.5 s; (d) t=1.0 s; (e) t=1.5 s; (f) t=3.0 s

4 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

(2+1)维色散长波方程的新孤子解及其演化下载： 1132次